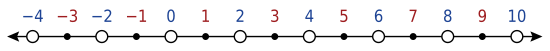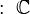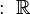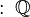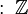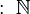Cero para niños
Datos para niños 0 |
||||
|---|---|---|---|---|
| Cardinal | Cero | |||
| Sistemas de numeración | ||||
| Arábiga oriental | ٠ | |||
| Ática | O | |||
| Jónica | Ο | |||
| China | 零/〇 | |||
| Egipcia |
|
|||
| Maya |  |
|||
| India | 0 | |||
| Sistema binario | 0 | |||
| Sistema octal | 0 | |||
| Sistema hexadecimal | 0 | |||
| Lista de números | ||||
.jpg)
El cero (0) es un símbolo numérico que representa la ausencia de cantidad. Es un número par. En los sistemas de numeración donde la posición de un dígito importa (como el nuestro), el cero ocupa los lugares donde no hay un valor significativo. Por ejemplo, en el número 10, el cero indica que no hay unidades, pero el 1 está en la posición de las decenas.
Si pones un cero a la derecha de un número entero, su valor se multiplica por 10 (por ejemplo, 5 se convierte en 50). Si lo pones a la izquierda, el número no cambia (05 sigue siendo 5).
El cero se usa en operaciones matemáticas como sumas, restas y multiplicaciones. Sin embargo, al representar "nada", puede causar situaciones especiales en matemáticas, como divisiones que no tienen un resultado claro.
El cero es el número que está entre el –1 y el 1 en la recta numérica de los números enteros.
Contenido
El Cero: Un Número Especial
El cero es un concepto fundamental en las matemáticas. Nos ayuda a entender la ausencia de algo y es clave en cómo escribimos y usamos los números hoy en día.
¿De dónde viene la palabra "cero"?
La palabra "cero" llegó al español desde el italiano zero. Esta, a su vez, viene de una palabra en latín, zephyrum. El origen más antiguo es la palabra sánscrita shunya, que significa "vacío". Los árabes la tradujeron como ṣifr.
El matemático italiano Leonardo Fibonacci (alrededor de 1170-1250) fue importante para traer el sistema decimal a Europa. Él usó el término zephyrum, que luego se convirtió en zefiro y finalmente en zero en Venecia. La palabra española "cifra" también viene directamente de la palabra árabe ṣifr.
¿Cómo se usaba el cero en la antigüedad?
Muchas civilizaciones antiguas, como la egipcia, la babilónica y la maya, tenían símbolos para indicar la ausencia de valor. Sin embargo, no siempre lo usaban de la misma manera que nosotros hoy.
- En Babilonia: El cero apareció por primera vez en Babilonia alrededor del año 400 a.C. Usaban un sistema de base 60. Al principio, no tenían un símbolo para el cero, lo que a veces causaba confusión. Más tarde, comenzaron a usar un signo de "dos cuñas" o "tres ganchos" para indicar un espacio vacío.
- En Mesoamérica: Las civilizaciones mesoamericanas, como la maya, también desarrollaron el concepto de cero antes de la era cristiana. El primer uso documentado del cero con un valor posicional (donde su lugar importa) fue en el año 36 a.C. en la numeración maya.
- En Roma: Los romanos no usaban el cero en su sistema de numeración. Sus números eran letras (I, V, X, L, C, D, M).
El cero posicional: Un gran avance
La civilización india fue clave para desarrollar la notación posicional, que es la forma en que escribimos los números hoy. El matemático indio Brahmagupta (siglo VI) fue uno de los primeros en pensar en el cero no solo como "nada", sino como un número que podía sumarse a números positivos y negativos.
El primer registro del "cero indio" es del año 683, en una inscripción en Camboya. Los árabes llevaron este conocimiento a Europa a través del Magreb y Al-Ándalus.
Aunque algunos creen que el cero llegó a Europa en el año 1000, la mayoría de las fuentes dicen que fue introducido por el matemático italiano Leonardo Fibonacci en el siglo XII. Él lo explicó en su libro Liber abaci. Al principio, algunas autoridades no lo aceptaron fácilmente.
¿Cómo se representa el cero?
El cero se representa con la cifra "0". En la informática, a veces se ve con una barra diagonal (Ø) para no confundirlo con la letra "O".
En un plano de coordenadas, el punto de partida (el origen) se asocia con el valor 0.
El cero y los números naturales
Existe un debate sobre si el cero pertenece al conjunto de los números naturales. Algunos matemáticos lo incluyen (llamándolos ℕ0), mientras que otros no (llamándolos ℕ+). Históricamente, el cero apareció mucho después que los otros números, lo que contribuye a esta discusión.
Operaciones matemáticas con el cero
Sumar con cero
Cuando sumas cualquier número a con 0, el resultado es el mismo número a.
- Ejemplo: 25 + 0 = 25.
Restar con cero
Si restas 0 a un número a, el resultado es el mismo número a. Pero si restas un número a a 0, el resultado es -a.
- Ejemplos: 37 – 0 = 37; 0 - 37 = -37.
Multiplicar por cero
Cualquier número multiplicado por 0 siempre da 0.
- Ejemplo: 25 × 0 = 0.
Dividir con cero
Puedes dividir 0 entre cualquier otro número, y el resultado siempre será 0.
- Ejemplo: 0 : 25 = 0.
Sin embargo, ¡no se puede dividir ningún número entre cero! Esto se llama una indeterminación y no tiene sentido en matemáticas. Imagina que tienes 8 manzanas y quieres repartirlas entre 0 personas; simplemente no se puede hacer.
Potencias con cero
- Cualquier número (excepto el 0) elevado a la potencia de 0 es igual a 1. Por ejemplo, 50 = 1.
- 0 elevado a cualquier potencia mayor que 0 es igual a 0. Por ejemplo, 03 = 0.
La expresión 00 es un caso especial y su valor no está definido de forma única.
¿Es el cero un número par?
Sí, el 0 es un número par. Cumple con la definición de número par y se comporta como tal en las matemáticas. Está justo en medio de los números impares –1 y 1.
El cero en la ciencia
Sistemas digitales
En los sistemas digitales y la informática, el 0 se usa para representar el estado de "apagado" o "falso". Es uno de los dos dígitos (0 y 1) del sistema binario, que es la base de cómo funcionan las computadoras.
Cero absoluto
En física, el cero absoluto es la temperatura más baja que se puede alcanzar. Es el punto de partida de la escala Kelvin (0 K), que equivale a -273.15 °C. A esta temperatura, las partículas de la materia tendrían la menor energía posible.
Galería de imágenes
-
Glifo maya para el cero.
-
Glifo maya para el cero, año 36 a.C. Es el primer uso documentado del cero utilizando notación posicional.
-
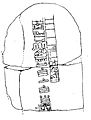
El reverso de la estela C de la cultura Epi Olmeca de Tres Zapotes, la segunda fecha más antigua descubierta del calendario mesoamericano de la cuenta larga. Los números 7.16.6.16.18 se traducen a septiembre de 32 años antes de Cristo.
-
Esta es una representación del cero expresado en chino contar varillas, basada en el ejemplo proporcionado por A History of Mathematics. Se utiliza un espacio vacío para representar el cero.
Véase también
En inglés: Zero Facts for Kids
