William Rowan Hamilton para niños
Datos para niños William Rowan Hamilton |
||
|---|---|---|
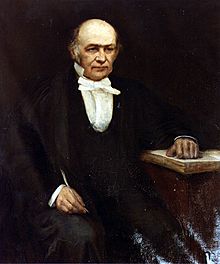 |
||
| Información personal | ||
| Nacimiento | 4 de agosto de 1805 Dublín (Reino Unido de Gran Bretaña e Irlanda) |
|
| Fallecimiento | 2 de septiembre de 1865 Dublín (Reino Unido de Gran Bretaña e Irlanda) |
|
| Sepultura | Mount Jerome Cemetery | |
| Nacionalidad | Británica | |
| Religión | Anglicanismo | |
| Familia | ||
| Padre | Archibald Rowan-Hamilton | |
| Cónyuge | Helen Maria Bayly | |
| Hijos | 3 | |
| Educación | ||
| Educación | Grado en Artes y Master of Arts | |
| Educado en | Trinity College Dublin (1823-1826) | |
| Información profesional | ||
| Ocupación | Matemático, físico, astrónomo, académico, profesor universitario y físico teórico | |
| Área | Matemáticas, mecánica, astronomía, física, física matemática, óptica y cuaternión | |
| Cargos ocupados | Royal Astronomer of Ireland (1827-1865) | |
| Empleador |
|
|
| Obras notables |
|
|
| Miembro de |
|
|
| Distinciones |
|
|
William Rowan Hamilton (nacido en Dublín el 4 de agosto de 1805 y fallecido en la misma ciudad el 2 de septiembre de 1865) fue un brillante matemático, físico y astrónomo irlandés. Hizo contribuciones muy importantes en campos como la óptica, la dinámica (el estudio del movimiento) y el álgebra.
Sus descubrimientos más famosos son los cuaterniones y su forma de organizar la dinámica. Este último trabajo fue clave para el desarrollo de la mecánica cuántica, donde un concepto fundamental llamado hamiltoniano lleva su nombre.
Contenido
La Vida de William Rowan Hamilton
Sus Primeros Años y Talentos
William Rowan Hamilton fue el cuarto de nueve hijos de Sarah y Archibald Hamilton. Su padre era abogado en Dublín. Desde los tres años, William vivió con su tío, James Hamilton, quien era un lingüista y dirigía una escuela.
Se dice que William mostró un talento increíble desde muy pequeño. A los siete años, ya había aprendido bastante hebreo. Antes de cumplir los trece, bajo la guía de su tío, conocía casi tantos idiomas como años tenía. Esto incluía idiomas clásicos y modernos de Europa, así como persa, árabe, hindustaní, sánscrito y otros. Mantuvo gran parte de este conocimiento toda su vida, leyendo en persa y árabe para relajarse.
Cuando tenía 9 años, William compitió en aritmética mental con un niño prodigio estadounidense llamado Zerah Colburn. Colburn ganó, y esta experiencia motivó a Hamilton a dedicar más tiempo a las matemáticas.
Su Educación y Carrera
Hamilton ingresó al Trinity College (Dublín) a los 18 años. Allí obtuvo calificaciones excepcionales. Estudió tanto clásicos como matemáticas. Mientras aún era estudiante, fue nombrado profesor de Astronomía y Astrónomo Real de Irlanda. Se mudó al Observatorio Dunsink, donde trabajó el resto de su vida.
Momentos Importantes en su Vida
Durante sus años universitarios, Hamilton propuso matrimonio a la hermana de un amigo, pero ella lo rechazó. Esto lo afectó mucho. Más tarde, en 1831, fue rechazado de nuevo por otra persona. Finalmente, en 1833, se casó con Helen Marie Bayly, con quien tuvo tres hijos: William Edwin, Archibald Henry y Helen Elizabeth.
Uno de los momentos más famosos de su vida ocurrió en 1843. Hamilton llevaba mucho tiempo pensando en un problema matemático. Un día, mientras paseaba con su esposa por el puente de Brongham en Dublín, la solución a los cuaterniones se le ocurrió de repente. Estaba tan emocionado que grabó la fórmula con su navaja en una piedra del puente. Aunque la inscripción original no se conserva, una placa conmemora este importante descubrimiento.
Fallecimiento y Legado
William Rowan Hamilton mantuvo su mente brillante hasta el final de su vida. Continuó trabajando en su libro "Elementos de los cuaterniones". Falleció el 2 de septiembre de 1865, a causa de una enfermedad. Fue enterrado en el cementerio Mount Jerome en Dublín.
Hamilton es considerado uno de los científicos más importantes de Irlanda. Se cuenta una anécdota, que podría ser una mezcla de realidad y leyenda, de que se le permitía caminar sobre el césped de la universidad, algo prohibido para los demás. Esto muestra lo mucho que se le respetaba como uno de los grandes matemáticos de su época.
En su honor, el Instituto Hamilton se dedica a la investigación matemática en la Universidad Maynooth. La Real Academia de Irlanda organiza una conferencia anual en su memoria. En 2005, el gobierno irlandés celebró el "Año de Hamilton" para conmemorar el 200 aniversario de su nacimiento. El Trinity College (Dublín) también inauguró el Instituto William Rowan Hamilton ese año.
Irlanda ha emitido sellos y una moneda de plata para celebrar sus logros. Además, los talleres de mantenimiento del sistema de tranvías de Dublín, llamados LUAS, llevan su nombre.
Contribuciones de Hamilton a la Ciencia
Su Trabajo en Astronomía
Desde joven, Hamilton tuvo un telescopio y se hizo experto en calcular fenómenos celestes, como los eclipses de luna. A los 21 años, en 1827, fue elegido Astrónomo Real de Irlanda y se mudó al Observatorio de Dunsink.
Al principio, Hamilton observaba el cielo con regularidad. Sin embargo, la astronomía observacional de entonces, que consistía en medir posiciones de estrellas, no era tan interesante para su mente matemática. Además, a menudo se enfermaba después de observar. Por eso, dejó la observación a su asistente.
Aunque hoy no se le conoce principalmente como astrónomo, sus conferencias de introducción a la astronomía eran muy populares. Atraían a estudiantes, eruditos, poetas e incluso a damas, algo notable en su tiempo.
Sus Descubrimientos en Física
Hamilton hizo grandes aportaciones a la óptica y a la mecánica clásica (el estudio del movimiento de objetos grandes). Su primer descubrimiento importante fue sobre las "Cáusticas", presentado en 1823.
En 1827, propuso una teoría que unía la mecánica, la óptica y las matemáticas, conocida hoy como ecuación de Hamilton-Jacobi. Esta teoría ayudó a establecer la teoría ondulatoria de la luz. Un resultado sorprendente de su trabajo fue la predicción de que un rayo de luz que entra en un tipo específico de cristal saldría como un cono hueco de rayos, un fenómeno llamado "refracción cónica".
Hamilton aplicó sus métodos de la óptica a la dinámica. Desarrolló el importante principio de la "acción variable". Aunque otros científicos como Joseph-Louis Lagrange ya habían estudiado principios similares, el análisis de Hamilton reveló una estructura matemática mucho más profunda. Sus avances permitieron resolver muchos más problemas de mecánica y son considerados una de las mayores contribuciones a la dinámica desde los trabajos de Isaac Newton y Lagrange.
La mecánica hamiltoniana es una forma poderosa de trabajar con las ecuaciones del movimiento. Es fundamental para estudiar sistemas físicos, desde los clásicos hasta los de la mecánica cuántica. Sus técnicas se usan en electromagnetismo, teoría de la relatividad y teoría cuántica de campos.
Sus Logros en Matemáticas
Los estudios matemáticos de Hamilton fueron en gran parte autodidactas. No siguió ninguna "escuela" matemática específica. Era muy bueno en aritmética y le gustaba hacer cálculos con muchos decimales.
A los diez años, encontró una copia en latín de los "Elementos" de Euclides y la estudió con entusiasmo. A los doce, leyó la "Arithmetica Universalis" de Isaac Newton, lo que lo introdujo al análisis moderno. A los dieciséis, ya dominaba gran parte de los "Principia" de Newton y otros trabajos avanzados.
Hamilton encontró un error en una de las demostraciones del famoso matemático Pierre-Simon Laplace. Un amigo lo animó a escribir sus comentarios, que fueron mostrados al Dr. John Brinkley, el Astrónomo Real de Irlanda, quien reconoció de inmediato el talento de Hamilton y lo apoyó.
Su carrera universitaria fue excepcional. Fue el mejor en todas las materias y exámenes. Obtuvo la rara distinción de ser sobresaliente tanto en griego como en física. A los 22 años, fue nombrado Profesor Andrews de Astronomía en la Universidad de Dublín.
Recibió la Medalla Cunningham de la Real Academia de Irlanda dos veces, en 1834 y 1848. También recibió la Medalla Real de la Royal Society en 1835. Fue elegido presidente de la Real Academia de Irlanda en 1837 y miembro de la Academia de Ciencias de Rusia. En 1864, la Academia Nacional de Ciencias de los Estados Unidos lo puso en la cima de su lista de miembros extranjeros.
El Descubrimiento de los Cuaterniones
La otra gran contribución de Hamilton a las matemáticas fue el descubrimiento de los cuaterniones en 1843. Antes, en 1840, Olinde Rodrigues ya había llegado a un resultado similar.
Hamilton buscaba una forma de extender los números complejos (que se pueden representar como puntos en un plano de dos dimensiones) a dimensiones espaciales más altas. No encontró un sistema útil para tres dimensiones, pero al trabajar con cuatro dimensiones, creó los cuaterniones.
Como se mencionó antes, el 16 de octubre de 1843, mientras paseaba con su esposa por el Royal Canal en Dublín, la solución se le ocurrió de repente en forma de ecuación:
- i2 = j2 = k2 = ijk = −1
Rápidamente grabó esta ecuación en el Broom Bridge. Este momento marcó el descubrimiento del grupo del cuaternión.
El líder irlandés Éamon de Valera, quien también era matemático, inauguró una placa conmemorativa en el puente en 1958. Desde 1989, la Universidad Nacional de Irlanda, Maynooth, organiza un paseo llamado Hamilton Walk, donde los matemáticos caminan desde el Observatorio de Dunsink hasta el puente para recordar este evento.
Los cuaterniones implicaron dejar de lado la conmutatividad (el orden de los factores no altera el producto), lo cual fue un paso muy innovador para la época. Hamilton también inventó los productos escalar y vectorial en el álgebra vectorial. Acuñó las palabras "tensor" y "escalar", y fue el primero en usar la palabra "vector" en su sentido moderno.
Cuando falleció, estaba trabajando en una explicación definitiva de los cuaterniones. Su hijo, William Edwin Hamilton, publicó el libro "Elementos de cuaterniones" en 1866.
Hoy en día, los cuaterniones se usan en computación gráfica, teoría del control, procesamiento de señales y mecánica orbital. Son muy útiles para representar rotaciones y orientaciones, por ejemplo, en sistemas de control de naves espaciales, porque son más estables numéricamente que otros métodos.
Algunos matemáticos modernos creen que el trabajo de Hamilton sobre los cuaterniones fue parodiado por Lewis Carroll en su famoso libro "Las aventuras de Alicia en el país de las maravillas". Se piensa que la fiesta del té del Sombrerero Loco podría representar la complejidad de los cuaterniones.
Otros Trabajos Importantes
Hamilton solía desarrollar sus ideas completamente en su mente antes de escribirlas. Además de sus grandes descubrimientos, dejó una enorme colección de notas y libros con ideas originales.
Desarrolló el principio variacional, que luego fue mejorado por Carl Gustav Jakob Jacobi. También creó el juego Icosian o "rompecabezas de Hamilton", que se resuelve usando el concepto de un camino hamiltoniano.
Sus investigaciones sobre la solución de ecuaciones algebraicas de quinto grado y su estudio de las funciones fluctuantes (importantes en la física) son otras de sus contribuciones. También inventó la hodógrafa, una herramienta para estudiar el movimiento.
Hamilton mantenía una correspondencia muy extensa. A menudo, una sola carta suya podía tener cincuenta o cien páginas, dedicadas a analizar un problema en detalle. Siempre fue amable al responder a quienes le pedían ayuda para entender sus obras. Era muy cuidadoso con la publicación de sus propios trabajos, lo que explica por qué publicó menos de lo que investigó.
Conceptos Nombrados en su Honor
Muchos conceptos y lugares llevan el nombre de William Rowan Hamilton:
- La mecánica hamiltoniana, una forma de describir la mecánica clásica.
- El principio de Hamilton, la ecuación de Hamilton-Jacobi y el teorema de Cayley-Hamilton.
- El hamiltoniano, que es una función en física y un concepto en la teoría de grafos.
- El camino hamiltoniano, otro concepto en la teoría de grafos.
- La 'Sociedad de Hamilton', una organización de estudiantes de medicina en Irlanda.
- El álgebra de cuaterniones se representa con la letra H o
 .
. - El edificio Hamilton en el Trinity College de Dublín.
- El cráter lunar Hamilton.
Publicaciones Destacadas
- Hamilton, William Rowan (Astrónomo Real de Irlanda), Introductory Lecture on Astronomy. Dublin University Review and Quarterly Magazine Vol. I, Trinity College, enero de 1833.
- Hamilton, William Rowan, Lectures on Quaternions. Royal Irish Academy, 1853.
- Hamilton (1866) Elements of Quaternions University of Dublin Press. Editado por William Edwin Hamilton, hijo del autor.
- Hamilton (1899) Elements of Quaternions volumen I, (1901) volumen II. Editado por Charles Jasper Joly; Longmans, Green & Co..
- Colección de David R. Wilkins de Hamilton's Mathematical Papers Archivado el 30 de mayo de 2013 en Wayback Machine..
Galería de imágenes
Véase también
 En inglés: William Rowan Hamilton Facts for Kids
En inglés: William Rowan Hamilton Facts for Kids



