Al-Karaŷí para niños
Abū Bakr Muḥammad ibn al-Ḥasan al-Karaŷí (conocido como al-Karají) fue un brillante matemático e ingeniero persa que vivió hace muchos siglos, entre los años 953 y 1029 aproximadamente. Pasó la mayor parte de su vida en Bagdad, una ciudad que en su época era un centro muy importante para la ciencia y el comercio en el mundo islámico.
Al-Karají escribió tres libros muy importantes sobre matemáticas. Sus títulos se pueden traducir como La maravilla del cálculo, Lo glorioso del álgebra y Lo suficiente del cálculo. Aunque hay algunas dudas sobre la forma exacta de su nombre debido a que no se conservan muchos escritos antiguos, lo que sí sabemos es que fue una mente privilegiada.
Contenido
¿Quién fue al-Karají y qué hizo?
Al-Karají fue un ingeniero y matemático de altísimo nivel. Aunque se basó en el trabajo de otros matemáticos que vivieron antes que él, fue el primero en hacer algo muy importante: liberó el álgebra de las ideas de la geometría. Antes, el álgebra se mezclaba mucho con las formas y figuras, como lo hacían los matemáticos griegos. Al-Karají cambió esto, usando operaciones que son la base del álgebra que conocemos hoy.
El álgebra: ¡una nueva forma de pensar!
En sus libros sobre álgebra, al-Karají explicó las reglas para hacer operaciones con polinomios. Los polinomios son expresiones matemáticas que combinan números y letras, como 2x + 3y. Se cree que él fue el primero en introducir la idea del cálculo algebraico, que es una forma de trabajar con estas expresiones de manera más abstracta.
Descubriendo patrones numéricos
Al-Karají también investigó los coeficientes binomiales y el famoso triángulo de Pascal. Estos son patrones numéricos que aparecen cuando multiplicas expresiones como (a+b) por sí mismas varias veces. Además, usó un método llamado inducción matemática para demostrar que sus resultados eran correctos. La inducción es como una escalera: si demuestras que puedes subir el primer escalón y que, si estás en un escalón, puedes subir al siguiente, entonces puedes subir todos los escalones.
Sus aportaciones a las matemáticas y la ingeniería son reconocidas todavía hoy. Por ejemplo, él descubrió una regla para formar los números del triángulo de Pascal: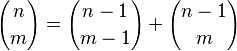 
Y también la fórmula para expandir expresiones como (a+b) elevado a una potencia 'n': 
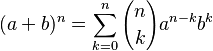Aunque a veces se piensa que Isaac Newton fue el primero en descubrir esta expansión, en realidad al-Karají la encontró para números enteros. Newton lo que hizo fue extenderla para números que no son enteros.
Un truco para calcular raíces cuadradas
Al-Karají también nos dejó una regla para calcular la raíz cuadrada de un número de forma aproximada. Si tienes un número N, y 'a²' es el cuadrado más grande que cabe dentro de N, y 'r' es lo que sobra, entonces la raíz cuadrada de N se puede aproximar con esta fórmula: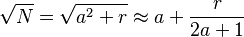 
Esta fórmula es una forma ingeniosa de acercarse al valor de una raíz cuadrada sin usar una calculadora.
Galería de imágenes
-
Diagrama realizado por al-Karjí
Véase también
En inglés: Al-Karaji Facts for Kids
- Matemática en el islam medieval
- Teorema del binomio
- Isaac Newton
