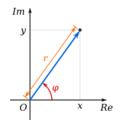Número complejo para niños
Los números complejos son un tipo especial de números que van más allá de los números que ya conoces, como los enteros o los decimales. Se representan con el símbolo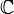 
. Imagina que los números que usas normalmente (los números reales, como 1, 2.5 o -3) son solo una parte de un grupo mucho más grande. Los números complejos incluyen a todos esos números reales y añaden algo nuevo: los números imaginarios.
Cada número complejo se forma combinando un número real y un número imaginario. La parte imaginaria siempre lleva una letra especial, la 
, que es la unidad imaginaria. Esta tiene una propiedad muy curiosa: si la multiplicas por sí misma (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): i \cdot i o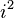 
), el resultado es -1. Esto es algo que no ocurre con los números reales, ya que cualquier número real multiplicado por sí mismo (sea positivo o negativo) siempre da un resultado positivo o cero.
Los números complejos son herramientas muy importantes en muchas áreas de las matemáticas y la ciencia. Se usan en el estudio de las ondas (como las de radio o las de sonido), en la electricidad, en la física (especialmente en la mecánica cuántica) y en la ingeniería. Ayudan a resolver problemas que serían muy difíciles o imposibles de solucionar solo con números reales.
Contenido
¿Qué son los números complejos?
Los números complejos son una extensión de los números reales. Esto significa que los números reales son un subconjunto de los números complejos. Puedes pensar en ellos como un conjunto más grande que contiene a los números que ya conoces.
Un número complejo se escribe generalmente como 
, donde:
es la parte real del número. Es un número real normal.
es la parte imaginaria del número. También es un número real, pero va acompañado de la unidad imaginaria .
Por ejemplo, en el número complejo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 + 2i , el 3 es la parte real y el 2 es la parte imaginaria.
¿Para qué se usan los números complejos?
Los números complejos son muy útiles en diferentes campos:
- Matemáticas: Ayudan a resolver ecuaciones que no tienen solución en los números reales, como encontrar la raíz cuadrada de un número negativo.
- Física: Se usan para describir el comportamiento de las ondas, la electricidad y el magnetismo. También son fundamentales en la mecánica cuántica, que estudia el mundo de las partículas muy pequeñas.
- Ingeniería: Son esenciales en la ingeniería eléctrica y electrónica para analizar circuitos de corriente alterna y señales.
Un poco de historia: ¿Cómo surgieron los números complejos?
La idea de los números complejos apareció por primera vez en el siglo XVI en Italia. Los matemáticos de esa época estaban tratando de resolver ecuaciones muy complicadas, especialmente las de tercer grado (donde la incógnita está elevada a la potencia de 3).
El enigma de las ecuaciones cúbicas
A veces, al intentar resolver estas ecuaciones, los matemáticos se encontraban con la raíz cuadrada de un número negativo. Esto era un gran problema, porque sabían que no se podía obtener un número real al elevarlo al cuadrado y que el resultado fuera negativo.
El matemático italiano Gerolamo Cardano fue uno de los primeros en encontrarse con este problema alrededor de 1545. Aunque no los entendía del todo, se dio cuenta de que, si trabajaba con estas "cantidades imposibles", a veces podía llegar a soluciones reales correctas para las ecuaciones.
El nacimiento de la unidad imaginaria
Más tarde, otro matemático italiano, Rafael Bombelli, desarrolló reglas para sumar, restar y multiplicar estos nuevos números. Él fue clave para que se empezaran a usar de forma más organizada.
En 1637, el filósofo y matemático René Descartes fue quien acuñó el término "imaginario" para estas cantidades, porque le parecían que solo existían en la imaginación. Sin embargo, con el tiempo, se demostró que eran muy reales y útiles.
La representación visual y el avance
Fue en el siglo XVIII cuando los números complejos empezaron a usarse más ampliamente. Matemáticos como Leonhard Euler descubrieron fórmulas muy importantes que conectaban los números complejos con las funciones trigonométricas (como el seno y el coseno), simplificando muchos cálculos.
La idea de ver los números complejos como puntos en un plano, llamado el plano complejo, fue propuesta por Caspar Wessel en 1799 y luego por Jean-Robert Argand en 1806. Finalmente, Carl Friedrich Gauss en 1831 popularizó esta forma de verlos, lo que ayudó a que fueran aceptados y entendidos por más matemáticos. Esta representación visual hizo que fueran mucho más fáciles de trabajar.
¿Cómo se definen los números complejos?
Un número complejo se puede definir como un par de números reales, por ejemplo,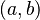 
.
- El primer número, , es la parte real y se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \text{Re}(z) .
- El segundo número, , es la parte imaginaria y se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \text{Im}(z) .
Si la parte imaginaria es cero (
), el número complejo es un número real, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (5,0) que es igual a 5. Si la parte real es cero (
), el número es un número imaginario puro, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (0,3) .
La unidad imaginaria 'i'
La unidad imaginaria se define como el número complejo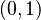 
. La propiedad más importante de es que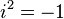 
. Esto se puede ver así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): i^2 = i \cdot i = (0,1) \cdot (0,1) = (-1,0) = -1
Operaciones básicas con números complejos
Los números complejos se pueden sumar, restar, multiplicar y dividir.
- Suma: Para sumar dos números complejos, sumas sus partes reales y sus partes imaginarias por separado.
- Resta: Para restar, restas sus partes reales y sus partes imaginarias por separado.
- Multiplicación: La multiplicación es un poco más compleja, pero sigue una regla definida.
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (a, b) \cdot (c, d) = (ac - bd, ad + bc)
El plano complejo: un mapa para los números
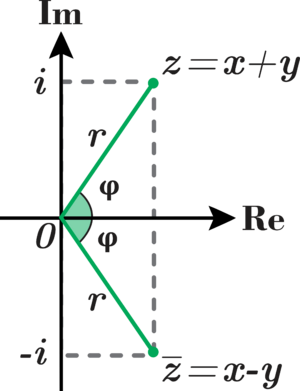
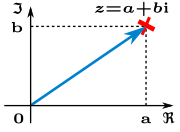
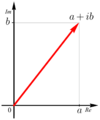
es la expresión binomial del punto.El plano complejo (también conocido como diagrama de Argand) es una forma visual de representar los números complejos. Es como un mapa donde cada número complejo es un punto.
- El eje horizontal se usa para la parte real ().
- El eje vertical se usa para la parte imaginaria ().
Así, el número complejo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 + 2i se representaría como el punto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (3,2) en este plano.
Módulo y argumento: otras formas de ver un número complejo
Además de la forma (llamada forma binómica), los números complejos también se pueden representar de otras maneras:
- Módulo (o valor absoluto): Es la distancia desde el origen (el punto 0,0) hasta el punto que representa el número complejo en el plano. Se calcula con el teorema de Pitágoras: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |z| = \sqrt{a^2 + b^2} .
- Argumento (o fase): Es el ángulo que forma la línea desde el origen hasta el punto del número complejo con el eje horizontal positivo.
Estas dos medidas (módulo y argumento) nos dan la forma polar de un número complejo, que es muy útil para multiplicaciones y divisiones.
El conjugado de un número complejo
El conjugado de un número complejo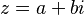 
es otro número complejo que tiene la misma parte real, pero la parte imaginaria con el signo opuesto. Se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \bar{z} = a - bi . Por ejemplo, el conjugado de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 + 2i es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 - 2i . Los conjugados son útiles para dividir números complejos.
Aplicaciones de los números complejos
En matemáticas: soluciones de ecuaciones
Una de las aplicaciones más importantes de los números complejos es que permiten resolver cualquier ecuación polinómica. El Teorema Fundamental del Álgebra dice que cualquier ecuación polinómica de grado 
(donde la potencia más alta de la incógnita es ) tiene exactamente soluciones en el conjunto de los números complejos. Esto significa que siempre podemos encontrar todas las soluciones si usamos números complejos.
En física e ingeniería: ondas y señales
Los números complejos son ideales para describir fenómenos que tienen un comportamiento de onda, como:
- Electricidad: En los circuitos de corriente alterna, los números complejos simplifican el análisis de cómo se comportan los componentes como resistencias y condensadores. Los ingenieros eléctricos suelen usar la letra
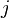en lugar de para la unidad imaginaria, para no confundirla con la intensidad de corriente. - Ondas: Permiten representar la amplitud (la "altura" de la onda) y la fase (la posición de la onda en un momento dado) de una señal de forma muy compacta.
- Mecánica cuántica: La matemática detrás de la mecánica cuántica, que describe el comportamiento de las partículas subatómicas, se basa en los números complejos.
Fractales
Muchos objetos fractales, como el famoso conjunto de Mandelbrot, se crean y estudian usando propiedades de los números complejos. Estos fractales son figuras geométricas que se repiten a diferentes escalas y tienen una complejidad asombrosa.
Galería de imágenes
-
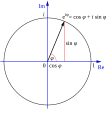
La fórmula de Euler ilustrada en el plano complejo.
-
Diagrama de Argand
-
El argumento φ y módulo r localizan un punto en un diagrama de Argand;
o 
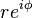es la expresión polar del punto.
Véase también
En inglés: Complex number Facts for Kids
