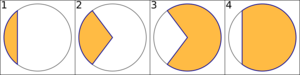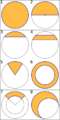Círculo para niños
.svg)
Un círculo es una figura geométrica plana. Imagina que tienes un punto fijo en el centro y dibujas todos los puntos que están a una distancia igual o menor de ese centro. Esa área que encierras es el círculo.
Es importante no confundir el círculo con la circunferencia. La circunferencia es solo el borde o el contorno del círculo, como el límite de un campo de fútbol. El círculo, en cambio, es toda la superficie que está dentro de ese borde. La circunferencia solo tiene longitud, mientras que el círculo tiene un área.
Contenido
- ¿Cuáles son las partes principales de un círculo?
- ¿Cómo se calcula el perímetro de un círculo?
- ¿Cómo se calcula el área de un círculo?
- Propiedades importantes del círculo
- ¿Cómo se relacionan las rectas con un círculo?
- ¿Cómo se relacionan los círculos entre sí?
- Ángulos especiales en un círculo
- Regiones especiales dentro de un círculo
- Galería de imágenes
- Véase también
¿Cuáles son las partes principales de un círculo?
Un círculo tiene varias partes importantes que te ayudarán a entenderlo mejor:
El centro del círculo
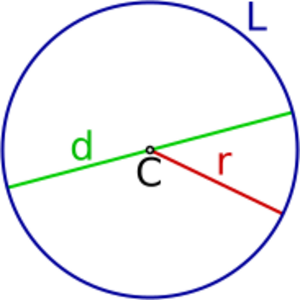
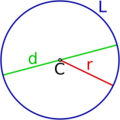
El centro es el punto que está exactamente en medio del círculo. Todos los puntos de la circunferencia (el borde) están a la misma distancia de este centro. En los dibujos, se suele representar con la letra C.
El radio del círculo
Un radio es una línea recta que va desde el centro del círculo hasta cualquier punto de su circunferencia. La longitud de esta línea también se llama radio y se representa con la letra r. El radio es la mitad de largo que el diámetro.
El diámetro del círculo
Un diámetro es una línea recta que une dos puntos de la circunferencia y que siempre pasa por el centro del círculo. La longitud de esta línea también se llama diámetro y se representa con la letra d. El diámetro es el doble de largo que el radio.
El perímetro del círculo
El perímetro de un círculo es la longitud de su contorno, es decir, la medida de la circunferencia que lo rodea. Se representa con la letra L.
La cuerda del círculo
Una cuerda es cualquier línea recta que une dos puntos de la circunferencia. Si una cuerda pasa por el centro, ¡entonces es el diámetro! El diámetro es la cuerda más larga que puede tener un círculo. En la imagen, la línea verde es una cuerda.
El arco del círculo
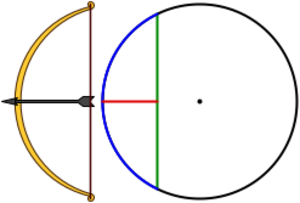
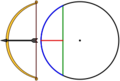
Un arco es una parte de la circunferencia, como un trozo de su borde. Está delimitado por dos puntos sobre la circunferencia. La línea curva azul en la imagen es un arco.
La flecha o sagita
La flecha (o sagita) es una línea que va desde el punto medio de una cuerda hasta el arco que esa cuerda "corta", sin pasar por el centro. Es el segmento rojo en la imagen.
¿Cómo se calcula el perímetro de un círculo?
El perímetro de un círculo es la longitud de su contorno. Para calcularlo, usamos una constante matemática muy especial llamada pi (π). El valor aproximado de pi es 3.14159.
La fórmula para el perímetro (p) es:
- Si conoces el radio (r): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p = 2 \cdot \pi \cdot r
- Si conoces el diámetro (d): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p = \pi \cdot d
Recuerda que el diámetro es el doble del radio (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d = 2 \cdot r ).
Ejemplo de cálculo del perímetro
Si un círculo tiene un diámetro de 2 unidades, su perímetro sería: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p = 2 \cdot \pi \approx 2 \cdot 3,14 = 6,28 unidades.
¿Cómo se calcula el área de un círculo?
El área de un círculo es la medida de la superficie que ocupa. Para calcularla, también usamos la constante pi (π).
La fórmula para el área (A) es:
- Si conoces el radio (r): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \pi \cdot r^2 (esto significa pi multiplicado por el radio al cuadrado)
- Si conoces el diámetro (d): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \frac{\pi \cdot d^2}{4}
Propiedades importantes del círculo
- Un círculo es simétrico: cualquier línea recta que pase por su centro es un eje de simetría. Esto significa que si doblas el círculo por esa línea, las dos mitades coincidirán perfectamente.
- Los círculos no cambian de forma si los giras alrededor de su centro. Siempre se ven igual, no importa cuánto los rotes.
¿Cómo se relacionan las rectas con un círculo?
Una línea recta puede tener diferentes posiciones respecto a un círculo:
- Una recta exterior es una línea que no toca el círculo en ningún punto. Está fuera de él. (Línea 'a' en la figura).
- Una recta tangente es una línea que toca el círculo en un solo punto. Es como si lo rozara. (Línea 'c' en la figura).
- Una recta secante es una línea que corta el círculo en dos puntos, dividiéndolo en dos partes. (Línea 'b' en la figura, con puntos A y B).
El punto donde una recta tangente toca el círculo se llama punto de tangencia. Una propiedad interesante es que cualquier recta tangente a un círculo es perpendicular al radio que llega hasta ese punto de tangencia.
¿Cómo se relacionan los círculos entre sí?
Los círculos también pueden tener diferentes posiciones entre ellos:
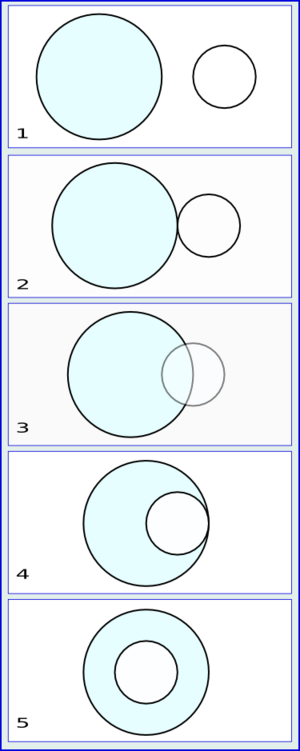
- Círculos disjuntos: No tienen ningún punto en común. Están separados. (Figura 1).
- Círculos tangentes exteriores: Se tocan en un solo punto por fuera. (Figura 2).
- Círculos interiores: Un círculo está completamente dentro del otro. (Figura 3).
- Círculos tangentes interiores: Un círculo está dentro del otro y se tocan en un solo punto. (Figura 4).
- Círculos excéntricos: Son círculos que no comparten el mismo centro. (Figura 4).
- Círculos concéntricos: Son círculos que tienen el mismo centro, pero radios diferentes. (Figura 5).
- Círculos coincidentes: Son círculos que tienen el mismo centro y el mismo radio, por lo que son exactamente iguales.
Una propiedad importante es que los centros de los círculos tangentes (ya sean exteriores o interiores) siempre están en la misma línea recta que el punto donde se tocan.
Ángulos especiales en un círculo
Podemos encontrar diferentes tipos de ángulos relacionados con un círculo:
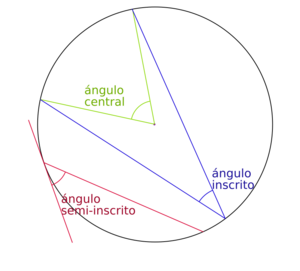
- Un ángulo central es el que tiene su vértice (la esquina del ángulo) justo en el centro del círculo.
- Un ángulo inscrito es el que tiene su vértice sobre la circunferencia (el borde del círculo), y sus lados son cuerdas del círculo.
- Un ángulo semiinscrito tiene su vértice en la circunferencia, uno de sus lados es una cuerda y el otro lado es una recta tangente al círculo en ese mismo vértice.
Regiones especiales dentro de un círculo
Un círculo se puede dividir en varias regiones con nombres específicos:
- El semicírculo es la mitad de un círculo, dividido por un diámetro. (Figura 1).
- El segmento circular es la parte del círculo que está entre una cuerda y el arco que esa cuerda "corta". (Figura 1).
- Un sector circular es una porción del círculo delimitada por dos radios y el arco que los une. Parece una porción de pizza. (Figura 5).
- La corona circular es la región que queda entre dos círculos concéntricos (que tienen el mismo centro). Parece un anillo. (Figura 6).
- El trapecio circular es una parte de la corona circular, delimitada por dos radios. (Figura 7).
- La lúnula es una región con forma de media luna, delimitada por dos circunferencias que se cortan. (Figura 8).
A veces, para ser más específicos, se habla de arcos, sectores o segmentos "menores" o "mayores":
- Un arco es menor si mide menos de la mitad de la circunferencia. Es mayor si mide más de la mitad.
- Un sector circular es menor si el ángulo central que lo forma es menor de 180 grados. Es mayor si el ángulo es mayor de 180 grados. (Figuras 2 y 3).
- Un segmento circular es menor si está delimitado por un arco menor. Es mayor si está delimitado por un arco mayor. (Figuras 1 y 4).
Galería de imágenes
-
Elementos de un círculo.
-
Cuerda, arco y flecha.
-
Tipos de rectas en relación con un círculo.
-
Posiciones relativas entre círculos.
-
Tipos de ángulos en un círculo.
-
Regiones de un círculo.
-
Arcos y sectores mayores y menores.
Véase también
En inglés: Circle Facts for Kids
