Teorema de Pitágoras para niños
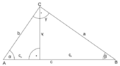
En matemáticas, el teorema de Pitágoras es una regla muy importante en la geometría que nos ayuda a entender la relación entre los lados de un triángulo rectángulo. Un triángulo rectángulo es aquel que tiene un ángulo recto (un ángulo de 90 grados).
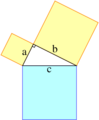
Este teorema dice que el área del cuadrado que se forma sobre el lado más largo del triángulo (llamado hipotenusa, que es el lado opuesto al ángulo recto) es igual a la suma de las áreas de los cuadrados que se forman sobre los otros dos lados (llamados catetos).
Si los catetos de un triángulo rectángulo miden a y b, y la hipotenusa mide c, la relación se escribe así:
(1)Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^2 + b^2 = c^2 \,
Esto significa que si conoces las medidas de dos lados de un triángulo rectángulo, puedes encontrar la medida del tercer lado. Es uno de los teoremas más famosos y útiles en las matemáticas.
El teorema de Pitágoras se ha demostrado de muchas maneras diferentes a lo largo de la historia, lo que lo hace aún más interesante. Algunas de estas demostraciones son muy antiguas.
Contenido
Historia del Teorema de Pitágoras
El teorema de Pitágoras lleva el nombre del filósofo y matemático griego Pitágoras, quien vivió en el siglo VI a. C.. Se cree que él y su escuela, los pitagóricos, fueron los primeros en demostrarlo de forma teórica.
Sin embargo, se sabe que civilizaciones mucho más antiguas, como los babilonios y los egipcios, ya conocían y usaban esta relación matemática. Por ejemplo, se han encontrado tablillas babilónicas de hace más de mil años antes de Pitágoras que muestran cómo usaban esta regla para resolver problemas.
En el Antiguo Egipto, la pirámide de Kefrén, construida alrededor del siglo XXVI a.C., se basó en un "triángulo sagrado egipcio" con proporciones 3-4-5. Esto significa que si los catetos medían 3 y 4 unidades, la hipotenusa medía 5 unidades, lo cual cumple con el teorema de Pitágoras (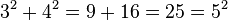 ). Aunque lo usaban, no se ha encontrado ningún documento que explique cómo llegaron a esta relación teóricamente.
). Aunque lo usaban, no se ha encontrado ningún documento que explique cómo llegaron a esta relación teóricamente.
¿Cómo se demuestra el Teorema de Pitágoras?
El teorema de Pitágoras es uno de los teoremas con más demostraciones diferentes. Se dice que existen más de mil formas de probarlo. En la Edad Media, incluso se pedía una nueva demostración de este teorema para obtener un título en matemáticas.
Las demostraciones pueden ser de varios tipos:
- Algebraicas: Usan ecuaciones y cálculos con números.
- Geométricas: Comparan áreas de figuras.
- Visuales: Muestran con dibujos cómo las áreas se relacionan.
Aquí te mostramos algunas de las demostraciones más conocidas:
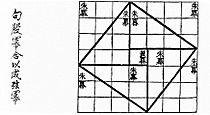
Demostración China: El Zhoubi Suanjing
En China, obras matemáticas antiguas como el Zhoubi Suanjing (escrito entre el 500 y el 300 a.C.) ya contenían una demostración visual del teorema.
Imagina un cuadrado grande. Dentro de él, puedes dibujar cuatro triángulos rectángulos iguales y un cuadrado más pequeño en el centro. Si los lados de los triángulos son a, b y la hipotenusa es c, el cuadrado central tendrá un lado que mide b - a.
El área del cuadrado grande es igual al área de los cuatro triángulos más el área del cuadrado pequeño. Si haces los cálculos, verás que esto lleva a la fórmula 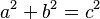 .
.
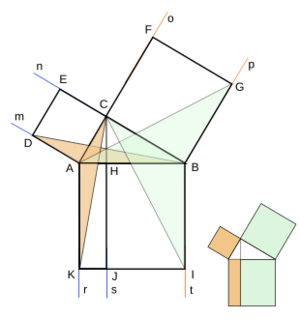
Demostración de Euclides
Euclides, un famoso matemático griego, incluyó una demostración del teorema de Pitágoras en su libro "Los Elementos". Su demostración es puramente geométrica y se basa en comparar las áreas de los cuadrados construidos sobre los lados del triángulo.
Euclides demostró que el área del cuadrado sobre la hipotenusa es igual a la suma de las áreas de los cuadrados sobre los catetos, dividiendo los cuadrados en rectángulos y triángulos y mostrando que sus áreas son equivalentes.
Demostración de Leonardo da Vinci
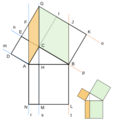
El famoso artista e inventor Leonardo da Vinci también ideó una demostración del teorema de Pitágoras. Su método es muy visual.
Imagina el triángulo rectángulo con los cuadrados en cada uno de sus lados. Leonardo añadió dos triángulos más, idénticos al original, para formar dos figuras más grandes. Luego, demostró que si quitas los triángulos de ambas figuras, las áreas restantes son iguales. Las áreas restantes son los dos cuadrados de los catetos en una figura y el cuadrado de la hipotenusa en la otra, demostrando así el teorema.
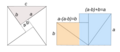
Demostración de Garfield
Incluso James A. Garfield, quien fue presidente de los Estados Unidos, desarrolló una demostración del teorema de Pitágoras.
Él construyó un trapecio usando tres triángulos rectángulos: dos iguales al original y uno más pequeño. Calculando el área del trapecio de dos maneras diferentes (una usando la fórmula del trapecio y otra sumando las áreas de los tres triángulos), y luego igualando esas expresiones, se llega a la fórmula 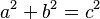 .
.
Usos del Teorema de Pitágoras
El teorema de Pitágoras es muy útil en muchas áreas de las matemáticas y en la vida real:
Triples Pitagóricos
Un triple pitagórico es un conjunto de tres números enteros positivos (a, b, c) que cumplen con la ecuación 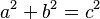 . Estos números representan las longitudes de los lados de un triángulo rectángulo donde todos los lados son números enteros.
. Estos números representan las longitudes de los lados de un triángulo rectángulo donde todos los lados son números enteros.
Algunos ejemplos conocidos son:
- (3, 4, 5) porque
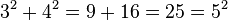
- (5, 12, 13) porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 5^2 + 12^2 = 25 + 144 = 169 = 13^2
Un triple pitagórico se llama "primitivo" si los tres números no tienen ningún divisor común aparte del 1.
Otros Ejemplos de Uso
- Calcular distancias: Puedes usarlo para saber la longitud de una escalera apoyada en una pared, si conoces la altura de la pared y la distancia de la base de la escalera a la pared.
- En geometría analítica: Sirve para encontrar la distancia entre dos puntos en un plano, usando sus coordenadas.
- En trigonometría: Es fundamental para demostrar la identidad trigonométrica básica que relaciona el seno y el coseno de un ángulo.
- En diseño y construcción: Ayuda a asegurar que las esquinas sean perfectamente cuadradas o a calcular dimensiones en estructuras.
Galería de imágenes
Véase también
 En inglés: Pythagorean theorem Facts for Kids
En inglés: Pythagorean theorem Facts for Kids