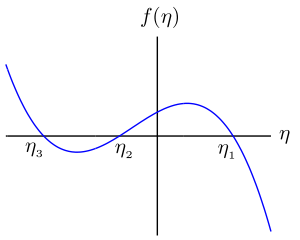
Resolución de ecuaciones para niños

En matemática, resolver una ecuación es como un juego de detectives. Consiste en encontrar los valores (que pueden ser números, funciones o conjuntos) que hacen que una igualdad sea cierta. Estos valores se llaman a menudo raíces de la ecuación o soluciones.

Una ecuación es una expresión que tiene una o más variables desconocidas, a las que llamamos incógnitas. Nuestro objetivo es reemplazar esas incógnitas con valores específicos para que la igualdad se cumpla. Para encontrar las soluciones, a veces necesitamos que las incógnitas pertenezcan a un conjunto numérico particular, como los números enteros o los números reales.

Por ejemplo, en la ecuación x + y = 2x - 1, si queremos resolverla para x, la solución sería x = y + 1. Esto significa que si sustituimos x por y + 1 en la ecuación original, la igualdad se mantiene. También podríamos resolverla para y, obteniendo y = x - 1.

A veces, una ecuación puede tener una única solución, varias soluciones o incluso infinitas soluciones. También puede que no tenga ninguna solución.

Resolver una ecuación numérica de una variable equivale a encontrar aquellos valores en el dominio de una función que la reducen a cero.

¿Qué es una Ecuación?

Una ecuación es una igualdad entre dos expresiones matemáticas. Imagina que tienes una balanza: lo que pones en un lado debe ser igual a lo que pones en el otro para que esté equilibrada. En una ecuación, los dos lados del signo igual (=) deben tener el mismo valor.

Por ejemplo, si tenemos la función f(x) = 3x - 2 y queremos que sea igual a 1, escribimos la ecuación:

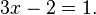
Aquí, x es nuestra incógnita, el valor que queremos descubrir.

¿Qué Significa Resolver una Ecuación?

Resolver una ecuación significa encontrar todos los valores de las incógnitas que hacen que la igualdad sea verdadera. El conjunto de todos esos valores se llama el conjunto solución.

Por ejemplo, para la ecuación 3x - 2 = 1, la única solución es x = 1. Si sustituimos x por 1, obtenemos 3(1) - 2 = 3 - 2 = 1, lo cual es cierto. Así, el conjunto solución es {1}.

El conjunto de soluciones puede ser:

• Vacío: No hay ninguna solución. Por ejemplo, la ecuación x² = -1 no tiene solución si x debe ser un número real, porque ningún número real elevado al cuadrado da un resultado negativo.
• Unitario: Hay exactamente una solución. Como en el ejemplo 3x - 2 = 1.
• Finito: Hay un número limitado de soluciones. Por ejemplo, x² = 4 tiene dos soluciones: x = 2 y x = -2.
• Infinito: Hay muchísimas soluciones. Por ejemplo, la ecuación x = x es verdadera para cualquier valor de x. A este tipo de igualdades se les llama identidades.

Métodos para Encontrar Soluciones

Existen muchos métodos para resolver ecuaciones, y el que usemos dependerá del tipo de ecuación. Algunos son sencillos y se pueden hacer con lápiz y papel, mientras que otros requieren herramientas más avanzadas o computadoras.

Prueba y Error

A veces, si el número de posibles soluciones es pequeño, podemos probar cada valor hasta encontrar el correcto. Esto es como adivinar, pero de forma organizada. Si una suposición no funciona, podemos aprender de ella para hacer una mejor suposición la próxima vez.

Álgebra Básica

Para ecuaciones sencillas con una sola incógnita, como 8x + 7 = 4x + 35, podemos usar las reglas básicas del álgebra elemental. Esto implica mover términos de un lado a otro del signo igual, cambiando su operación (sumar pasa a restar, multiplicar a dividir, etc.) para "despejar" la incógnita.

Sistemas de Ecuaciones Lineales

Cuando tenemos varias ecuaciones con varias incógnitas que están relacionadas, hablamos de un sistema de ecuaciones lineales. Los sistemas pequeños se pueden resolver con álgebra básica, pero para sistemas más grandes se usan métodos más avanzados del álgebra lineal.

Ecuaciones Polinómicas

Las ecuaciones que involucran polinomios (expresiones con sumas y restas de términos con potencias de la incógnita, como x², x³, etc.) hasta el grado cuatro (es decir, con la incógnita elevada a la cuarta potencia como máximo) tienen fórmulas para encontrar sus soluciones. La fórmula cuadrática es un ejemplo para ecuaciones de segundo grado. Sin embargo, para ecuaciones de grado cinco o superior, no existe una fórmula general que funcione siempre.

Funciones Inversas

Si tenemos una ecuación como h(x) = c (donde c es un número), podemos usar la función inversa de h para encontrar x. Una función inversa "deshace" lo que hace la función original. Si aplicamos la función inversa a ambos lados de la ecuación, podemos aislar x.

Por ejemplo:

• Si x está sumando, restamos el mismo número a ambos lados.
• Si x está multiplicando, dividimos por el mismo número a ambos lados.
• Si x es un exponente (como en 2^x = 8), usamos el logaritmo.
• Si x es la base de una potencia (como x³ = 27), usamos la raíz correspondiente.

Factorización

Si podemos reescribir un lado de la ecuación como una multiplicación de expresiones (factorizar), podemos encontrar las soluciones igualando cada una de esas expresiones a cero. Por ejemplo, si P = QR, entonces las soluciones de P = 0 son las soluciones de Q = 0 y las soluciones de R = 0.

Métodos Numéricos

Para ecuaciones muy complicadas, a veces no podemos encontrar una solución exacta. En estos casos, usamos métodos numéricos para encontrar una solución aproximada. Estos métodos usan algoritmos (pasos repetitivos) para acercarse cada vez más a la solución real. Un ejemplo es el método de Newton.

Ecuaciones con Matrices

Las ecuaciones que usan matrices y vectores (que son arreglos de números) se resuelven con métodos del álgebra lineal.

Ecuaciones Diferenciales

Las ecuaciones diferenciales son un tipo especial de ecuaciones que involucran derivadas de funciones. Se usan para describir cómo cambian las cosas con el tiempo o el espacio. Hay muchos métodos para resolverlas, tanto exactos como aproximados.

Resolución de Otras Ecuaciones

El mundo de las ecuaciones es muy amplio. Podemos encontrar ecuaciones que usan operadores diferenciales, matrices y otros conceptos matemáticos avanzados. En todos los casos, el objetivo sigue siendo el mismo: encontrar los valores que hacen que la igualdad sea verdadera. Lo que cambia es la estrategia o el método que necesitamos usar para lograrlo.

Véase también

En inglés: Equation solving Facts for Kids

• Ecuación
• Ecuación diferencial
• Análisis matemático
• Análisis numérico
• Sistema de ecuaciones
• Resolución numérica de ecuaciones no lineales
• Completar el cuadrado