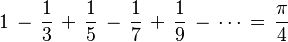Gottfried Leibniz para niños
Datos para niños Gottfried Leibniz |
||
|---|---|---|
 Retrato de Gottfried Leibniz, por Christoph Bernhard Francke. Museo Herzog Anton Ulrich, Brunswick.
|
||
| Información personal | ||
| Nombre en alemán | Gottfried Wilhelm Leibniz | |
| Nacimiento | 1 de julio de 1646 Leipzig,  Electorado de Sajonia (actual  Alemania) |
|
| Fallecimiento | 14 de noviembre de 1716 Hannover, .svg){kind=small} Electorado de Hannover (actual Alemania) |
|
| Sepultura | Neustädter Hof- und Stadtkirche St. Johannis | |
| Religión | Luteranismo | |
| Lengua materna | Alemán | |
| Familia | ||
| Padres |
|
|
| Educación | ||
| Educación | Grado en Artes, Maestría en Artes, Grado en Leyes, habilitación universitaria, Doctor de Leyes y doctor en Filosofía | |
| Educado en |
|
|
| Supervisor doctoral | Jakob Thomasius, Erhard Weigel, Bartholomäus Leonhard Schwendendörffer y Christiaan Huygens | |
| Alumno de |
|
|
| Información profesional | ||
| Área | Filosofía, matemáticas, política | |
| Conocido por | Padre del cálculo | |
| Cargos ocupados |
|
|
| Empleador | Universidad de Leipzig | |
| Estudiantes doctorales | Nicolas Malebranche y Christian Wolff | |
| Alumnos | Jakob Bernoulli y Johann Bernoulli | |
| Movimiento | Racionalismo | |
| Obras notables |
|
|
| Miembro de |
|
|
| Distinciones |
|
|
| Firma | ||
 |
||
| Notas | ||
| Sostuvo conflictos con Isaac Newton por la paternidad del cálculo. | ||
Gottfried Wilhelm Leibniz (nacido en Leipzig el 1 de julio de 1646 y fallecido en Hannover el 14 de noviembre de 1716) fue un pensador muy importante. Fue filósofo, matemático, lógico, teólogo, jurista, bibliotecario y diplomático.
Se le conoce como el "último genio universal" porque fue la última persona que logró aprender mucho sobre casi todos los campos del conocimiento de su época. Después de él, las personas empezaron a especializarse en un solo campo. Leibniz hizo grandes aportes en metafísica (el estudio de la realidad), epistemología (el estudio del conocimiento), lógica, filosofía de la religión, matemáticas, física, geología, jurisprudencia (leyes) e historia.
Incluso otros pensadores importantes de su tiempo admiraban sus logros. Por ejemplo, Denis Diderot, un filósofo francés, escribió que quizás nadie había leído, estudiado, meditado y escrito tanto como Leibniz. Sus ideas sobre el mundo, Dios, la naturaleza y el alma eran muy profundas.
Leibniz es muy importante tanto en la historia de la filosofía como en la historia de las matemáticas. Él desarrolló el cálculo infinitesimal y su forma de escribirlo, que es la que usamos hoy. Hizo esto de forma independiente al trabajo de Isaac Newton, quien lo había desarrollado antes pero no lo había publicado. Leibniz también inventó el sistema binario, que es la base de cómo funcionan las computadoras modernas. Fue uno de los primeros en Europa en reconocer el valor del pensamiento chino y la importancia de China.
Leibniz, junto con René Descartes y Baruch Spinoza, son considerados los tres grandes pensadores racionalistas del siglo XVII. Su filosofía también se conecta con ideas antiguas y anticipa la lógica y la filosofía analítica modernas. También contribuyó a la tecnología y predijo ideas que aparecieron mucho después en biología, medicina, geología, teoría de la probabilidad, psicología y ciencias de la computación. Sus muchos escritos, incluyendo miles de cartas y manuscritos, muestran la gran variedad de sus intereses.
Contenido
- Biografía de Gottfried Leibniz
- Obras de Leibniz
- Reconocimiento póstumo
- Filosofía de Leibniz
- Actividades científicas
- Matemática
- Eponimia
- Véase también
Biografía de Gottfried Leibniz
Primeros años y educación
Gottfried Leibniz nació el 1 de julio de 1646 en Leipzig, dos años antes de que terminara la Guerra de los Treinta Años. Su padre, Friedrich Leibniz, era profesor de filosofía en la Universidad de Leipzig. Su madre era Catharina Schmuck.
Cuando tenía seis años, su padre falleció. Su educación quedó en manos de su madre, su tío y, según él mismo, de su propio esfuerzo. Su padre le dejó una biblioteca personal que Leibniz pudo usar libremente desde los siete años. Allí leyó mucho sobre historia antigua y escritos religiosos.
A los doce años, ya había aprendido latín por sí mismo y había empezado a estudiar griego. En 1661, con catorce años, entró a la Universidad de Leipzig. Terminó sus estudios a los veinte, especializándose en leyes y mostrando un gran dominio de los clásicos, la lógica y la filosofía. Sin embargo, su formación en matemáticas no era tan avanzada como la de otros países.
En 1666, publicó su primer libro y su tesis, llamada Disertación acerca del arte combinatorio. Como la universidad no le ofreció un puesto de profesor de leyes, Leibniz presentó su tesis a la Universidad de Altdorf y obtuvo su doctorado en solo cinco meses. Rechazó una oferta de trabajo en Altdorf y dedicó el resto de su vida a servir a dos importantes familias nobles de Alemania.
Al servicio de la Casa de Schönborn (1666-1674)
Asesor en Maguncia
El primer trabajo de Leibniz fue como ayudante en Núremberg, aunque no sabía nada del tema. Allí conoció a Johann Christian von Boineburg, un antiguo ministro del Electorado de Maguncia. Von Boineburg lo contrató como asistente y lo presentó al elector. Leibniz le dedicó un ensayo al elector, esperando conseguir un empleo. Su plan funcionó, y el elector le pidió ayuda para reescribir las leyes de su territorio. En 1669, fue nombrado asesor de la Corte de Apelaciones. Aunque von Boineburg murió en 1672, Leibniz siguió trabajando para su viuda hasta 1674.
Von Boineburg ayudó mucho a la reputación de Leibniz. Su trabajo con el elector pronto se volvió más diplomático. Leibniz propuso un plan para proteger a Alemania de las ambiciones del rey Luis XIV de Francia. Sugirió que Francia tomara Egipto para distraerla de atacar Alemania y los Países Bajos. El elector apoyó el plan con cautela. En 1672, el gobierno francés invitó a Leibniz a París para hablar del tema, pero el plan no se llevó a cabo.
Estancias en París y Londres
Así, Leibniz pasó varios años en París, donde aprendió mucho sobre matemáticas y física, y empezó a hacer sus propias contribuciones. Conoció a importantes filósofos y matemáticos, como Nicolas Malebranche y Christiaan Huygens. Al principio, Leibniz se dio cuenta de que sus conocimientos en física y matemáticas eran incompletos. Con la ayuda de Huygens, estudió mucho por su cuenta y pronto hizo grandes descubrimientos, incluyendo su versión del cálculo diferencial y su trabajo con series infinitas.
_07.jpg)
A principios de 1673, Leibniz viajó a Londres en una misión diplomática. Allí conoció a Henry Oldenburg y John Collins. Presentó ante la Royal Society una máquina que había diseñado y construido desde 1670, llamada Stepped Reckoner. Esta fue la primera máquina capaz de hacer las cuatro operaciones aritméticas básicas. La Sociedad lo nombró miembro externo. La misión terminó de repente al saber de la muerte del elector. Leibniz regresó a París.
La muerte de sus dos protectores hizo que Leibniz buscara un nuevo trabajo. En 1669, el duque de Brunswick lo había invitado a Hannover. Leibniz rechazó la invitación entonces, pero empezó a escribirse con el duque en 1671. En 1673, el duque le ofreció un puesto de consejero, que Leibniz aceptó dos años después, cuando vio que no conseguiría trabajo en París ni en la corte de los Habsburgo.
Al servicio de la Casa de Hannover (1676-1716)
Segundo viaje a Londres y consejero político
Leibniz logró retrasar su llegada a Hannover hasta finales de 1676. Antes, hizo un breve viaje a Londres, donde pudo haber visto algunos trabajos no publicados de Isaac Newton. Aunque la mayoría de los historiadores creen que Newton y Leibniz desarrollaron sus ideas de forma independiente: Newton las desarrolló primero y Leibniz fue el primero en publicarlas.
En su viaje de Londres a Hannover, se detuvo en La Haya, donde conoció a Anton van Leeuwenhoek, quien mejoró el microscopio y descubrió los microorganismos. También pasó varios días discutiendo con Baruch Spinoza, un filósofo importante. Leibniz respetaba la inteligencia de Spinoza, pero no estaba de acuerdo con sus ideas, que contradecían las creencias cristianas.
En 1677, Leibniz fue ascendido a consejero privado de Justicia, un cargo que mantuvo toda su vida. Sirvió a tres gobernantes de la Casa de Brunswick como historiador, consejero y bibliotecario de la Biblioteca Ducal. Escribió mucho sobre asuntos políticos, históricos y religiosos relacionados con la Casa de Brunswick.
Entre las pocas personas que apoyaron a Leibniz en el norte de Alemania estaban la electora Sofía Carlota de Hannover y Carolina de Brandeburgo-Ansbach. Para ellas, Leibniz fue un amigo y consejero.
Hannover era una ciudad pequeña de unos 10.000 habitantes, y a Leibniz no le gustaba su ambiente provinciano. Sin embargo, ser un cortesano importante en la Casa de Brunswick era un gran honor, especialmente porque la Casa ganó mucho prestigio durante la relación de Leibniz con ella. En 1692, el duque de Brunswick se convirtió en elector del Sacro Imperio Romano Germánico. La Ley de Asentamiento de 1701 designó a la electora Sofía y a sus descendientes como la familia real del Reino Unido. Leibniz participó en las negociaciones para esta ley.
Trabajos intelectuales y últimos años
Los gobernantes de Brunswick permitieron que Leibniz dedicara mucho tiempo a sus proyectos intelectuales, como mejorar el cálculo, escribir sobre matemáticas, lógica, física y filosofía, y mantener una gran cantidad de cartas. Empezó a trabajar en el cálculo en 1674 y en 1677 ya tenía un sistema completo, pero no lo publicó hasta 1684. Sus trabajos más importantes de matemáticas se publicaron entre 1682 y 1692, principalmente en una revista que él y Otto Mencke habían fundado, la Acta Eruditorum. Esta revista fue clave para su reputación científica y matemática, lo que a su vez aumentó su importancia en la diplomacia, historia, teología y filosofía.
El elector Ernesto Augusto le encargó a Leibniz escribir la historia de la Casa de Brunswick, esperando que el libro ayudara a sus ambiciones. Entre 1687 y 1690, Leibniz viajó mucho por Alemania, Austria e Italia buscando documentos para este proyecto. Pasaron las décadas y el libro no se terminaba, lo que molestó al siguiente elector. Leibniz nunca lo terminó, en parte por sus muchos otros trabajos y por su insistencia en hacer una investigación muy detallada. Sus patrones solo querían un libro corto y popular. Sin embargo, cuando los escritos de Leibniz se publicaron en el siglo XIX, resultaron ser tres volúmenes.
El 23 de enero de 1698, murió Ernesto Augusto y le sucedió su hijo Jorge Luis. Leibniz se encontró con un príncipe que no valoraba su trabajo. Leibniz buscaba cualquier excusa para dejar Hannover. Su único consuelo era su amistad con Sofía Carlota de Hannover y su madre, la princesa Sofía del Palatinado.
En 1711, John Keill acusó a Leibniz de haber copiado el cálculo de Newton, lo que inició una larga disputa sobre quién lo había inventado primero. La Royal Society investigó y apoyó las acusaciones de Keill.
Ese mismo año, el zar ruso Pedro el Grande visitó Hannover y se reunió con Leibniz, quien se interesó por los asuntos rusos el resto de su vida. En 1712, Leibniz pasó dos años en Viena, donde fue nombrado consejero de la Corte imperial.
Tras la muerte de la reina Ana en 1714, el elector Jorge Luis se convirtió en el rey Jorge I de Gran Bretaña. Aunque Leibniz había ayudado mucho a esta causa, no fue reconocido. A pesar de la intervención de la princesa de Gales Carolina de Brandeburgo-Ansbach, Jorge I le prohibió a Leibniz reunirse con él en Londres hasta que hubiera terminado al menos un volumen de la historia de la familia Brunswick. Además, la presencia de Leibniz en la corte de Londres habría molestado a Newton, quien era visto como el ganador de la disputa sobre el cálculo. Su querida amiga y protectora, la electora Sofía de Wittelsbach, también murió en 1714.
Fallecimiento
.JPG)
En junio de 1716, Leibniz se encontró por última vez con Pedro el Grande. Después, sufrió mucho de gota y tuvo que quedarse en cama hasta su muerte. Leibniz falleció en Hannover en noviembre de ese año. Para entonces, había caído en desgracia en la Corte, y ni Jorge I ni ningún otro cortesano, salvo su secretario personal, asistieron a su funeral. Aunque Leibniz era miembro de la Royal Society y de la Academia Prusiana de las Ciencias, ninguna de las dos lo honró.
Su tumba permaneció sin identificar hasta que Bernard Le Bovier de Fontenelle lo elogió ante la Academia de Ciencias de Francia, que lo había aceptado como miembro extranjero en 1700.
Resumen cronológico de la vida de Leibniz
| Año | Suceso o evento |
|---|---|
|
Años de formación y estudios. |
|
Trabaja principalmente para el obispo elector de Maguncia, Juan Felipe de Schönborn. |
|
Vive en París y realiza dos viajes importantes a Londres. |
|
Sirve a la casa de Hannover. |
|
Es cortesano, primero de Juan Federico, duque de Brunswick-Luneburgo,
y luego de su hermano, el duque y elector Ernesto Augusto de Hanover. |
|
Viaja por Alemania, Austria e Italia para investigar la historia de la Casa de Brunswick. |
|
Es cortesano del elector Jorge Luis de Hanover. |
|
Vive en Viena. Es nombrado consejero de la Corte imperial en 1713 por |
|
Jorge Luis, al convertirse en Jorge I de Gran Bretaña, le prohíbe a Leibniz
seguirlo a Londres. Leibniz pasa sus últimos años en relativo olvido. |
Obras de Leibniz
Leibniz escribió principalmente en tres idiomas: latín (alrededor del 40%), francés (alrededor del 35%) y alemán (menos del 25%). Durante su vida, publicó muchos folletos y artículos académicos, pero solo dos libros de filosofía: Disertación acerca del arte combinatorio y la Théodicée.
Publicó muchos folletos, a menudo sin firmar, en nombre de la Casa de Brunswick. Uno importante fue De jure suprematum, que hablaba sobre la soberanía. Otro libro importante, Nouveaux essais sur l'entendement humain (Nuevos ensayos sobre el entendimiento humano), se publicó después de su muerte. Leibniz había decidido no publicarlo tras la muerte de John Locke, a quien respondía en el libro.
Hasta 1895, cuando se catalogaron sus manuscritos y cartas, no se supo la enorme cantidad de escritos que dejó: unas 15.000 cartas a más de 1.000 personas, además de otros 40.000 documentos. Muchas de sus cartas son tan largas como ensayos. Gran parte de su correspondencia sigue sin publicarse, y mucho de lo que se ha publicado es reciente. La gran cantidad y variedad de sus escritos se debe a que él mismo se sentía muy ocupado, como escribió en una carta:
No puedo terminar de decirles lo extraordinariamente distraído y disperso que soy. Estoy intentando hallar varias cosas en estos archivos; busco papeles antiguos y voy detrás de documentos sin publicar. Con esto espero arrojar alguna luz sobre la historia de la Casa de Brunswick. Recibo y respondo una inmensa cantidad de cartas. Al mismo tiempo tengo tantos resultados matemáticos, pensamientos filosóficos y otras innovaciones literarias, que no se debe permitir que se desvanezcan, que a menudo no sé por dónde comenzar.Carta de Leibniz a Vincent Placcius en Gerhardt, 1695.
Los escritos de Leibniz se están publicando en una edición completa, organizada en series:
- Serie 1. Correspondencia política, histórica y general.
- Serie 2. Correspondencia filosófica.
- Serie 3. Correspondencia matemática, científica y técnica.
- Serie 4. Escritos políticos.
- Serie 5. Escritos históricos y lingüísticos.
- Serie 6. Escritos filosóficos.
- Serie 7. Escritos matemáticos.
- Serie 8. Escritos científicos, médicos y técnicos.
La organización de todos los escritos de Leibniz comenzó en 1901. Dos guerras mundiales y la división de Alemania dificultaron mucho este gran proyecto, que debe manejar unos 200.000 documentos escritos en siete idiomas.
En 1985, el proyecto se reorganizó. Desde entonces, varias sedes en Alemania han publicado 25 volúmenes de la edición completa hasta 2006.
Reconocimiento póstumo
Cuando Leibniz falleció, su fama había disminuido. Solo se le recordaba por un libro, la Théodicée, cuyas ideas fueron malinterpretadas por Voltaire en su novela Cándido. La descripción de Voltaire fue tan influyente que muchas personas la tomaron como la verdad, lo que llevó a que las ideas de Leibniz no fueran bien entendidas. Además, un discípulo de Leibniz, el filósofo Christian Wolff, con su estilo dogmático, también contribuyó a dañar la reputación de Leibniz. En esa época, la filosofía se estaba alejando del racionalismo del siglo XVII, del que Leibniz fue un gran representante. Sus trabajos en derecho, diplomacia e historia fueron vistos como poco importantes, y la riqueza de su correspondencia fue ignorada.
En gran parte de Europa se dudaba de que hubiera descubierto el cálculo de forma independiente de Newton, y por eso se despreció todo su trabajo en matemáticas y física. Voltaire, que admiraba a Newton, también escribió Cándido para desacreditar la afirmación de Leibniz sobre el cálculo y su opinión de que la teoría de la gravitación universal de Newton era incorrecta. Sin embargo, el surgimiento de la relatividad y estudios posteriores sobre la historia de las matemáticas mostraron el trabajo de Leibniz de una manera más positiva.
El camino de Leibniz hacia su reconocimiento actual comenzó en 1765 con la publicación de sus Nouveaux Essais, que fueron leídos con atención por Immanuel Kant. En el siglo XIX, se publicaron varias ediciones de sus obras y su correspondencia con personas importantes.
En 1900, Bertrand Russell publicó un estudio sobre la metafísica de Leibniz, y poco después Louis Couturat publicó un estudio importante y editó escritos inéditos de lógica. Aunque algunas de estas conclusiones fueron cuestionadas, le dieron a Leibniz más respeto entre los filósofos del siglo XX. Hoy en día, la reputación de Leibniz como filósofo es quizás más alta que nunca.
Esto se debe a varias razones:
- Los estudios sobre la historia de las ideas de los siglos XVII y XVIII han mostrado la "Revolución intelectual" que precedió a la Revolución industrial.
- La filosofía actual valora más la metafísica.
- La filosofía analítica moderna sigue usando ideas de Leibniz sobre la identidad, la individuación y los mundos posibles.
- Se le ve como una continuación importante del esfuerzo de Platón y Aristóteles para entender el universo y el lugar del ser humano en él a través de la razón.
En 1985, el gobierno alemán creó el Premio Gottfried Wilhelm Leibniz, que se entrega anualmente. Es el premio más importante de Alemania para las contribuciones científicas.
En 1970, la Unión Astronómica Internacional nombró un cráter de impacto en la cara oculta de la Luna como «Leibniz» en su honor.
En 2006, la Universidad de Hannover fue renombrada «Gottfried Wilhelm Leibniz» en su honor.
Filosofía de Leibniz
El pensamiento filosófico de Leibniz se encuentra en muchos textos cortos: artículos, manuscritos publicados después de su muerte y muchas cartas. Solo escribió dos tratados de filosofía, y el que se publicó en vida, la Théodicée de 1710, es tanto teológico como filosófico.
Leibniz considera que su inicio como filósofo fue con su Discurso de metafísica, que escribió en 1686. Este texto y una discusión con Antoine Arnauld no se publicaron hasta el siglo XIX.
En 1695, Leibniz se dio a conocer en la filosofía europea con un artículo llamado Nuevo sistema de la naturaleza y comunicación de las sustancias. Entre 1695 y 1705, escribió sus Nuevos ensayos sobre el entendimiento humano, un comentario extenso sobre el libro de John Locke, Ensayo sobre el entendimiento humano. Pero al saber de la muerte de Locke en 1704, decidió no publicarlo, y los Nuevos ensayos no vieron la luz hasta 1765. La Monadología, otra de sus obras importantes, escrita en 1714 y publicada después de su muerte, tiene noventa aforismos (frases cortas que expresan una verdad).
Leibniz conoció a Baruch Spinoza en 1676 y leyó algunos de sus escritos no publicados. A diferencia de René Descartes, Leibniz y Spinoza tuvieron una educación filosófica muy completa. La influencia de sus profesores se nota en su forma de pensar. Leibniz también leyó mucho a Francisco Suárez, un jesuita español. Le interesaban los nuevos métodos de Descartes, Christiaan Huygens, Isaac Newton y Robert Boyle, pero los veía desde una perspectiva influida por ideas antiguas. Sin embargo, sus métodos y preocupaciones a menudo anticipan la lógica y la filosofía analítica del siglo XX.
Fue uno de los primeros pensadores europeos en reconocer el valor del pensamiento chino.
Los principios fundamentales
Leibniz usaba libremente nueve principios fundamentales en su filosofía:
- Identidad/contradicción: Si algo es verdadero, su opuesto es falso.
- Sustancia: Es lo que hace que algo sea individual y único. Es la unidad básica del mundo, con capacidad de sentir y desear, y sus características solo pueden venir de sí misma.
- Identidad de los indiscernibles: Dos cosas son idénticas si tienen exactamente las mismas propiedades. A este principio se le llama a menudo "ley de Leibniz".
- Principio de razón suficiente: Debe haber una razón para que cualquier cosa exista, para que cualquier evento ocurra, para que cualquier verdad sea cierta. Aunque a veces solo Dios conoce esa razón.
- Armonía preestablecida: La naturaleza de cada cosa hace que lo que le sucede a una corresponda a lo que les sucede a las otras, sin que actúen directamente entre sí. Por ejemplo, un vaso se rompe porque "sabe" que ha tocado el suelo, no porque el impacto lo obligue.
- Continuidad: La naturaleza no da saltos. Todo es continuo.
- Optimismo: Dios siempre elige lo mejor.
- Plenitud: El mejor de los mundos posibles haría realidad cada posibilidad verdadera.
- Principio de conveniencia: O "la elección de lo mejor", que se basa en la posibilidad, no en la necesidad.
Principio de razón suficiente
El principio de razón suficiente, explicado por Gottfried Leibniz en su Teodicea, dice que nada ocurre sin una razón suficiente para que sea así y no de otra manera. Esto significa que los eventos que parecen azarosos o casuales lo parecen porque no conocemos todas las causas que los provocaron.
Ahora debemos remontarnos a la metafísica, sirviéndonos del gran principio por lo común poco empleado, que afirma que nada se hace sin razón suficiente, es decir que nada sucede sin que le fuese imposible a quien conociera suficientemente las cosas, dar una razón que sea suficiente para determinar por qué es esto así y no de otra manera. Enunciado el principio, la primera cuestión que se tiene derecho a plantear será: por qué hay algo más bien que nada. Pues la nada es más simple y más fácil que algo. Además, supuesto que deban existir cosas, es preciso que se pueda dar razón de por qué deben existir de ese modo y no de otroGottfried Leibniz. Principios de la naturaleza, 7.
Este principio complementa el principio de no contradicción y se aplica a los hechos. Por ejemplo, si "César pasó el Rubicón", algo debió motivarlo.
Para Leibniz, este principio es la base de toda verdad, porque nos permite saber la razón de la verdad de una afirmación. Si todo lo que sucede tiene una razón, conociendo esa razón se podría saber lo que pasará en el futuro. Esta es la base de la ciencia experimental.
Sin embargo, debido a los límites de la mente humana, debemos aceptar que nada ocurre sin razón, aunque a menudo no podamos conocer esas razones.
Una consecuencia de este principio para la física fue que "en el mejor de los mundos posibles la naturaleza no da saltos y nada sucede de golpe". Esto conecta el principio con la idea de la continuidad y la infinita divisibilidad de la materia.
Las mónadas
La contribución más importante de Leibniz a la metafísica es su teoría de las mónadas, explicada en la Monadología. Las mónadas son los elementos más pequeños y básicos del universo, como los átomos lo son en el mundo físico. Son "formas de ser" con estas características: son eternas, no se pueden dividir, son individuales, siguen sus propias reglas, no interactúan entre sí y cada una es un reflejo de todo el universo en una armonía preestablecida.
Las mónadas son sustancias simples. No tienen tamaño ni espacio. Cada mónada es una sustancia espiritual, tiene un "deseo" y se desarrolla según su propia ley interna.
Las mónadas son centros de fuerza. El espacio, la materia y el movimiento son solo apariencias. El espacio es relativo, no absoluto, y consiste en cómo percibimos las relaciones espaciales entre las mónadas. Por ejemplo, vemos una silla frente a una mesa. No puede ser absoluto porque no hay una razón para que el universo esté en un lugar y no en otro. La idea de que las mónadas no tienen tamaño se explica porque si un objeto se dividiera por algo externo, estaría siendo modificado por una causa ajena, lo que iría en contra de la idea de que la sustancia se causa a sí misma. Esto se resuelve con el principio de armonía preestablecida, donde todo sucede en un orden simultáneo y coherente de "reflejos".
La característica principal de una mónada es que no se puede reducir. A diferencia de los átomos, las mónadas no son materiales ni espaciales. También son completamente independientes entre sí, por lo que las interacciones entre mónadas son solo aparentes. En cambio, gracias al principio de la armonía preestablecida, cada mónada sigue un conjunto de "instrucciones" preprogramadas, de modo que una mónada "sabe" qué hacer en cada momento. Estas "instrucciones" son como las leyes científicas que rigen las partículas subatómicas. Así, cada mónada es como un pequeño espejo del universo. Las mónadas son "pequeñas"; por ejemplo, cada ser humano es una mónada. Dios también es una mónada, y su existencia se puede deducir de la armonía entre las demás mónadas. Dios desea la armonía preestablecida.
Se cree que las mónadas resuelven problemas como:
- La interacción entre la mente y el cuerpo (un problema en el sistema de Descartes).
- La falta de individuación en el sistema de Spinoza, donde las criaturas individuales son solo accidentales.
La teoría de las mónadas fue vista como extraña en la época de Leibniz y desde entonces.
La existencia de Dios
El Dios de Leibniz no es el Motor inmóvil de Aristóteles, ni el "Gran Ser" de Isaac Newton. Es "un Dios vivo y personal que se revela tanto al corazón como a la razón", buscando así una base racional para el Dios cristiano. En la filosofía de Leibniz, hay cuatro tipos de argumentos sobre la existencia de Dios:
- El argumento ontológico (basado en la idea de Dios).
- El argumento cosmológico (basado en la existencia del universo).
- El argumento de las verdades eternas, inspirado por San Agustín.
- El argumento de la armonía preestablecida (o argumento fisicoteológico).
Leibniz creía que el concepto de Dios es posible y escribió varias formas del argumento ontológico de San Anselmo. En su Monadología escribió:
(41) “De donde se sigue que Dios es absolutamente perfecto, no siendo la perfección sino la magnitud de la realidad positiva, tomadas precisamente, dejando aparte los límites o linderos en las cosas que los tienen. Y donde no hay ningún límite, es decir, en Dios, la perfección es absolutamente infinita”.(44)“Pues si alguna realidad hay en las Esencias o posibilidades o bien en las verdades eternas, es preciso que dicha realidad esté fundada en algo existente y Actual, y, por consiguiente, en la Existencia del Ser necesario, en el cual la Esencia encierra la Existencia, o en el cual ser posible basta para ser Actual.
(45)Así, solo Dios (o el Ser necesario) goza del siguiente privilegio: es preciso que exista, si es posible. Y como nada puede impedir la posibilidad de lo que no tiene ningún límite, ninguna negación, y, por consiguiente, ninguna contradicción, esto solo basta para conocer la Existencia de Dios a priori…”.Monadología § 41, 44, 45 (1714)
Además, Leibniz formuló un argumento cosmológico basado en la contingencia (la idea de que las cosas podrían no haber existido) a favor de la existencia de Dios con su principio de razón suficiente en su Monadología. Él escribió: "No se puede encontrar ningún hecho que sea verdadero o existente, ni ninguna proposición verdadera, sin que haya una razón suficiente para que sea así y no de otra manera, aunque no podemos conocer estos motivos en la mayoría de los casos". Formuló el argumento cosmológicamente así: "¿Por qué hay algo en lugar de nada? La razón suficiente [...] se encuentra en una sustancia que [...] es un ser necesario que lleva la razón de su existencia dentro de sí mismo". Este argumento es uno de los más populares en la filosofía de la religión.
El argumento de las verdades eternas también se basa en el principio de razón suficiente: "las verdades eternas no tienen en sí mismas la razón de su existencia y, por tanto, esta debe buscarse en el Ser Supremo. [...] La razón suficiente de las verdades eternas es Dios mismo, ya que el conjunto de todas ellas no es otra cosa que el propio entendimiento divino". El argumento de la armonía preestablecida se basa en la armonía de las mónadas: "según Leibniz, el mundo y cada una de las criaturas que lo componen se desarrollan con sus propias fuerzas, pero estas últimas fueron creadas y elegidas por Dios de modo necesario para preestablecer la mejor organización del mundo".
La Teodicea y el optimismo
El término "optimismo" aquí se refiere a "óptimo" o "lo mejor", no al estado de ánimo.
La Teodicea intenta justificar las imperfecciones del mundo, afirmando que es el mejor de los mundos posibles. Debe ser el mejor y más equilibrado de los mundos posibles, ya que fue creado por un Dios perfecto.
La idea de "el mejor de los mundos posibles" se justifica por la existencia de un Dios con capacidad de ordenar, no de forma moral, sino matemáticamente. Para Leibniz, este es el mejor mundo posible, no en un sentido moral, sino matemáticamente, porque Dios, de infinitas posibilidades de mundos, encontró la más estable entre variedad y uniformidad. Es el mundo más perfecto matemática y físicamente.
La afirmación de que "vivimos en el mejor de los mundos posibles" le valió a Leibniz muchas burlas, especialmente de Voltaire, quien lo caricaturizó en su novela cómica Cándido. Allí, el personaje del Dr. Pangloss (una parodia de Leibniz) repite la frase como un mantra cada vez que les ocurre una desgracia. De ahí viene el adjetivo "panglosiano", para describir a alguien tan ingenuo como para creer que nuestro mundo es el mejor de los mundos posibles.
El matemático Paul du Bois-Reymond escribió que Leibniz pensaba en Dios como un matemático.
Como se sabe, la teoría de máximos y mínimos de las funciones está en deuda con él por el progreso, gracias al descubrimiento del método de las tangentes. Pues bien, concibe a Dios en la creación del mundo como un matemático resolviendo un problema de mínimos, o más bien, en nuestra fraseología moderna, un problema en el cálculo de las variaciones — siendo la cuestión determinar, entre un número infinito de mundos posibles, aquel en el cual se minimiza la suma del mal necesario.
Una defensa del optimismo de Leibniz se basa en principios científicos que surgieron después de su muerte, como el principio de mínima acción, la ley de conservación de la masa y la conservación de la energía.
Teoría del conocimiento
Las mónadas tienen percepciones, que pueden ser claras u oscuras. Las cosas tienen percepciones sin conciencia. Cuando las percepciones son claras, conscientes y van acompañadas de memoria, se llaman apercepción, propia de las almas. Las almas humanas pueden conocer verdades universales y necesarias. Así, el alma es espíritu. En la cima de las mónadas está la divina. Puedes encontrar más información sobre esto en la Monadología.
Leibniz distingue entre verdades de razón y verdades de hecho. Las primeras son necesarias, como "Dos y dos son cuatro". Las segundas no se justifican fácilmente, como "Colón descubrió América", porque pudo haber sido de otra manera. Pero Colón descubrió América porque estaba en su ser individual (mónada). Solo Dios conoce todas las verdades de hecho, porque su omnisciencia y omnipotencia le permiten ver todas las posibilidades. Solo Dios puede entender las verdades de hecho, ya que esto requiere un análisis infinito.
Leibniz creía en un tipo de innatismo en el conocimiento. Todas las ideas provienen de la actividad interna de cada mónada. Por lo tanto, las ideas son innatas. Leibniz se opuso a John Locke y a todo el empirismo inglés.
Pensamiento simbólico
Leibniz creía que gran parte del razonamiento humano podía reducirse a un tipo de cálculo, y que estos cálculos podían resolver muchas diferencias de opinión:
La única manera de rectificar nuestros razonamientos es hacerlos tan tangibles como los de los Matemáticos, para que podamos encontrar nuestro error de un vistazo, y cuando haya disputas entre personas, podemos simplemente decir: Calculemos [calculemus], sin mas dilación, a ver quien tiene razón.
El calculus ratiocinator de Leibniz, que se parece a la lógica simbólica, se puede ver como una forma de hacer posibles esos cálculos. Leibniz escribió notas que hoy se consideran intentos de crear la lógica simbólica y su "cálculo". Estos escritos no se publicaron hasta el siglo XIX.
Leibniz pensaba que los símbolos eran importantes para la comprensión humana. Le dio tanta importancia al desarrollo de buenas notaciones que atribuyó todos sus descubrimientos en matemáticas a esto. Su notación para el cálculo es un ejemplo de su habilidad. La pasión de Leibniz por los símbolos y la notación, y su creencia de que son esenciales para la lógica y las matemáticas, lo convirtieron en un precursor de la semiótica.
Pero Leibniz fue más allá. Definió un carácter como cualquier signo escrito, y un carácter "real" como uno que representa una idea directamente. Algunos caracteres reales, como la notación lógica, solo sirven para facilitar el razonamiento. Muchos caracteres conocidos en su época, como los jeroglíficos egipcios, los caracteres chinos y los símbolos de la astronomía y la química, no los consideraba reales. En cambio, propuso crear una characteristica universalis o "característica universal", basada en un alfabeto del pensamiento humano en el que cada concepto fundamental se representaría con un único carácter "real":
Es obvio que si pudiéramos encontrar caracteres o signos adecuados para expresar todos nuestros pensamientos con tanta claridad y exactitud como la aritmética expresa los números o la geometría expresa las líneas, podríamos hacer en todas las materias en cuanto están sujetas al razonamiento todo lo que podemos hacer en aritmética y geometría. Porque todas las investigaciones que dependan del razonamiento se realizarían por transposición de estos caracteres y por una especie de cálculo.
Los pensamientos complejos se representarían combinando caracteres más simples. Leibniz vio que la unicidad de la descomposición en factores primos sugería un papel central para los números primos en la característica universal, una anticipación sorprendente de la numeración de Gödel.
Al principio, Leibniz no concibió la "característica" como un álgebra, sino como un lenguaje o escritura universal. Recién en 1676 concibió una especie de "álgebra del pensamiento". La "característica" resultante incluía un cálculo lógico, combinatoria, álgebra, su analysis situs (geometría de la situación), un lenguaje conceptual universal y más. La idea de Leibniz de razonar a través de un lenguaje universal de símbolos y cálculos anticipa notablemente los grandes desarrollos del siglo XX en los sistemas formales.
Lógica formal
Leibniz es considerado uno de los lógicos más importantes entre los tiempos de Aristóteles y Gottlob Frege. Desarrolló la doctrina del análisis y la síntesis. Entendía la lógica como la ciencia de todos los mundos posibles. Leibniz fue el primero en formular la ley de la razón suficiente y también el autor de la expresión ley de identidad en la lógica moderna. Consideraba la ley de identidad como el principio supremo de la lógica: "La naturaleza de la verdad en general consiste en el hecho de que es algo idéntico".
La ley de identidad formulada por Leibniz se usa hoy en la mayoría de los cálculos lógico-matemáticos. El principio de sustitución es equivalente a la ley de identidad: "Si A es B y B es A, entonces A y B se llaman 'lo mismo'".
Para Leibniz, los principios de identidad, sustitución equivalente y contradicción son los medios principales de cualquier prueba lógica. Creía que los axiomas son frases que no se pueden probar y que son identidades.
Leibniz no publicó nada sobre lógica formal en vida; la mayor parte de lo que escribió son borradores. Bertrand Russell afirmó que Leibniz había desarrollado la lógica en sus escritos inéditos a un nivel que solo se alcanzó 200 años después.
El trabajo de Russell sobre Leibniz encontró que muchas de las ideas de Leibniz (por ejemplo, que cada mónada refleja todo el universo) se derivan de su decisión de considerar las relaciones entre las cosas como irreales. Él veía las relaciones como "cualidades" de las cosas. Por ejemplo, para él, "María es la madre de Juan" describe cualidades separadas de María y de Juan. Esto contrasta con la lógica relacional moderna. Leibniz también afirmó que el espacio y el tiempo son inherentemente relacionales.
El descubrimiento de Leibniz en 1690 de su "álgebra de conceptos" (equivalente al álgebra booleana) y la metafísica asociada, son importantes en la metafísica computacional actual.
Actividades científicas
Matemáticas
Antes de Leibniz, existían técnicas para resolver problemas de tangente, encontrar máximos y mínimos y calcular áreas, pero no había un sistema claro ni un simbolismo uniforme. Gottfried Leibniz unió estas técnicas en un solo sistema de conceptos de análisis interrelacionados, con una notación que permitía operar con cantidades muy pequeñas.
- 1675: Leibniz creó el cálculo diferencial e integral y publicó sus principales resultados antes que Newton, quien había llegado a resultados similares pero no los había publicado.
- 1684: Leibniz publicó el primer trabajo importante sobre Cálculo diferencial: "El nuevo método de máximos y mínimos". En este trabajo, no se menciona a Newton. Sus trabajos de análisis comenzaron a publicarse solo en 1704. Más tarde, surgió una larga disputa entre Newton y Leibniz sobre quién descubrió primero el cálculo diferencial.
El documento de Leibniz establece los conceptos básicos del cálculo diferencial y las reglas de diferenciación. Usando la interpretación geométrica, explica los signos de aumento y disminución, máximos y mínimos, convexidad y concavidad, y puntos de inflexión. Leibniz escribió: "Lo que una persona versada en este cálculo puede resolver en tres líneas, otros hombres eruditos se vieron obligados a buscar siguiendo complejos desvíos".
- 1686: Por primera vez, introdujo el símbolo
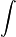para la integración, e indicó que esta operación es lo contrario de la diferenciación. - 1692: Introdujo el concepto de envolvente de una familia de curvas.
- 1693: Leibniz abordó el problema de resolver sistemas lineales; sus resultados introdujeron el concepto de determinante.
- 1695: Leibniz introdujo la función exponencial en su forma más general:
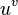. - 1702: Junto con Johann Bernoulli, Leibniz descubrió el método de descomposición en fracciones parciales, lo que resolvió muchos problemas de integración.
El enfoque de Leibniz para el análisis matemático tenía algunas características. Él veía el análisis de forma algebraica, a diferencia de Newton. En sus primeros artículos, parecía entender las cantidades infinitesimales como objetos reales. Al final de su vida, habló de variables potencialmente infinitas. En términos filosóficos, consideraba el infinitesimal como el soporte de la continuidad en la naturaleza. Los intentos de Leibniz de hacer un análisis riguroso no tuvieron éxito, y sus ideas sobre lo infinitamente pequeño causaron críticas.
Gottfried Wilhelm Leibniz demostró la solidez de sus métodos resolviendo varios problemas difíciles. Por ejemplo, en 1691, estableció que un hilo pesado colgando formaba una catenaria. También, junto con Isaac Newton y otros, resolvió el problema de la Curva braquistócrona en 1696.
Su extensa correspondencia fue importante para difundir sus ideas. Algunos descubrimientos los compartió solo por carta, como los inicios de la teoría de determinantes en 1693.
Leibniz introdujo muchos términos matemáticos que usamos hoy: "diferencial", "cálculo diferencial", "ecuación diferencial", "función", "variable", "constante", "coordenadas", "abscisa", "curvas algebraicas y trascendentales", "algoritmo". Aunque el concepto de función ya existía, Leibniz fue el primero en usarlo explícitamente para referirse a conceptos geométricos derivados de una curva.
Leibniz formuló el concepto de diferencial como una diferencia muy pequeña entre dos valores cercanos de una variable, y la integral como la suma de un número infinito de diferenciales. Dio las reglas más simples para la diferenciación e integración en sus notas de 1675. En 1684, en su primera memoria sobre cálculo diferencial, "Un nuevo método de máximos y mínimos", dio la definición y el signo del diferencial.
El ensayo de 1684 fue seguido por otros trabajos de Leibniz que cubren todas las divisiones básicas del cálculo diferencial e integral. En estas obras, definió la integral (1686), enfatizando que es la operación inversa a la diferenciación. También inició la integración de fracciones racionales (1702-1703). Además, Leibniz dio gran importancia al uso de series infinitas para estudiar funciones y resolver ecuaciones diferenciales (1693).
Debido a sus publicaciones anteriores y a su notación más clara, el trabajo de Leibniz sobre el cálculo diferencial e integral tuvo una influencia mucho mayor que la teoría de Newton. Incluso los compatriotas de Newton adoptaron gradualmente la notación de Leibniz.
Leibniz también describió sistemas binarios con los números 0 y 1. El sistema binario moderno fue descrito completamente por él en su obra Explication de l’Arithmétique Binaire. Como le interesaba la cultura china, Leibniz conoció el Libro de Cambios y notó que los hexagramas corresponden a números binarios. Admiró esto como una prueba de los logros chinos en matemáticas filosóficas.
Leibniz pudo haber sido el primer programador y teórico de la información. Descubrió que si se escriben ciertos grupos de números binarios uno debajo del otro, los ceros y unos en las columnas verticales se repiten regularmente, lo que le hizo creer que había nuevas leyes matemáticas. Se dio cuenta de que el código binario es ideal para un sistema mecánico. Intentó aplicar el código binario en la mecánica e incluso dibujó una computadora que funcionaba con sus nuevas matemáticas, pero se dio cuenta de que la tecnología de su tiempo no permitía crear una máquina así. Describió el proyecto de una computadora que operaba en el sistema binario, usando un prototipo de tarjeta perforada, en un trabajo de 1679. También escribió sobre la posibilidad de modelar las funciones del cerebro humano con máquinas.
Ciencias naturales
Al proponer que la Tierra tiene un núcleo fundido, se adelantó a la geología moderna. En embriología, creía que los organismos son el resultado de una combinación de un número infinito de microestructuras posibles. En las ciencias de la vida y la paleontología, mostró una sorprendente intuición sobre la transformación de las especies, gracias a su estudio de la anatomía comparada y los fósiles. Uno de sus principales trabajos sobre este tema, Protogaea, se publicó en inglés por primera vez recientemente. También desarrolló una teoría organísmica inicial. En medicina, animó a los médicos de su época a basar sus teorías en observaciones detalladas y experimentos verificados, y a distinguir claramente los puntos de vista científico y metafísico.
Psicología
La psicología fue un interés central para Leibniz. Se le considera un "pionero subestimado de la psicología". Escribió sobre temas que hoy son campos de la psicología: atención, conciencia, memoria, aprendizaje (asociación), motivación, la individualidad y el desarrollo general (psicología evolutiva). Sus discusiones en Nuevos ensayos y Monadología a menudo se basan en observaciones cotidianas, como el comportamiento de un perro o el ruido del mar, y desarrolla analogías intuitivas. También ideó principios que se aplican a la psicología: el continuo de las "pequeñas percepciones" (inconscientes) a la apercepción (consciente), y el paralelismo psicofísico (mente y cuerpo actúan por separado pero en armonía).
La posición de Leibniz sobre el conocimiento, en contra de John Locke y el empirismo inglés, era clara: "Nihil est in intellectu quod non fuerit in sensu, nisi intellectu ipse" – "Nada hay en el intelecto que no haya estado primero en los sentidos, excepto el intelecto mismo". Esto significa que principios que no están en las impresiones sensoriales pueden reconocerse en la percepción y la conciencia humanas: inferencias lógicas, categorías de pensamiento, el principio de causalidad y el principio de propósito.
Leibniz encontró a su intérprete más importante en Wilhelm Wundt, fundador de la psicología como disciplina. Wundt usó una cita de Leibniz en la portada de su libro y publicó una monografía sobre él. Wundt dio forma al término apercepción, introducido por Leibniz, en una psicología de la apercepción basada en la psicología experimental.
Gran parte del trabajo de Leibniz tuvo un gran impacto en la psicología. Leibniz pensaba que hay muchas percepciones pequeñas de las que no somos conscientes. Creía que la transición entre los estados consciente e inconsciente tenía pasos intermedios. Para que esto fuera cierto, también debe haber una parte de la mente de la que no somos conscientes en un momento dado. Su teoría sobre la conciencia en relación con el principio de continuidad puede verse como una teoría temprana sobre las etapas del sueño. De esta manera, la teoría de la percepción de Leibniz puede verse como una de las muchas teorías que llevaron a la idea del inconsciente. Leibniz influyó directamente en Ernst Platner, a quien se le atribuye haber acuñado el término "Unbewußtseyn" (inconsciente). Además, la idea de los estímulos subliminales se remonta a su teoría de las pequeñas percepciones. Las ideas de Leibniz sobre la música y la percepción tonal influyeron en los estudios de laboratorio de Wilhelm Wundt.
Matemática
Aunque la idea matemática de función ya existía en la trigonometría y las tablas logarítmicas de su época, Leibniz fue el primero, en 1692 y 1694, en usarla explícitamente para referirse a conceptos geométricos derivados de una curva, como la abscisa, ordenada, tangente, cuerda y perpendicular. Leibniz fue el primero en proponer usar un punto como signo de multiplicación en matemáticas, en lugar de la letra "x" que se usaba en Inglaterra. La letra "x" se usó desde entonces como nombre de variable, especialmente para el cálculo en tres dimensiones XYZ. En el siglo XVIII, el concepto de "función" perdió estas asociaciones puramente geométricas.
Leibniz fue el primero en ver que los números de un sistema de ecuaciones lineales podían organizarse en una tabla, ahora conocida como matriz, que podía manipularse para encontrar la solución del sistema. Este método se conoció más tarde como "eliminación gaussiana". Leibniz también contribuyó al álgebra booleana y la lógica simbólica.
Cálculo infinitesimal
La invención del cálculo infinitesimal se atribuye a Leibniz y Newton. Según los cuadernos de Leibniz, el 11 de noviembre de 1675 ocurrió un evento clave. Ese día, usó por primera vez el cálculo integral para encontrar el área bajo la curva de una función y=f(x).
Leibniz introdujo varias notaciones que se usan hoy, como el signo "integral" ∫, que es una S alargada de la palabra latina summa (suma), y la letra "d" para los "diferenciales", de la palabra latina differentia (diferencia). Esta notación ingeniosa y útil para el cálculo es probablemente su legado matemático más duradero. Actualmente, se usa la notación de cálculo creada por Leibniz, no la de Newton.
Leibniz no publicó nada sobre su cálculo hasta 1684. La regla del producto del cálculo diferencial todavía se llama "regla de Leibniz para la derivación de un producto". Además, el teorema que explica cómo diferenciar bajo el signo integral se llama la "regla de Leibniz para la derivación de una integral".
Desde 1711 hasta su muerte, la vida de Leibniz estuvo marcada por una larga disputa con John Keill, Newton y otros sobre si había inventado el cálculo independientemente de Newton, o si solo había inventado otra notación para las ideas de Newton. Leibniz pasó el resto de su vida tratando de demostrar que no había copiado las ideas de Newton.
Geometría
La fórmula de Leibniz para π/4 dice que:
Leibniz escribió que los círculos "pueden expresarse de la manera más simple mediante esta serie, es decir, el agregado de fracciones alternativamente sumadas y restadas". Sin embargo, esta fórmula solo es precisa con un gran número de términos. Leibniz intentó crear una definición para una línea recta al intentar probar el postulado de las paralelas. Aunque la mayoría de los matemáticos definían una línea recta como la línea más corta entre dos puntos, Leibniz creía que esto era solo una propiedad, no la definición.
Topología
Leibniz también publicó la idea de la ciencia que ahora se llama Topología, que estudia las propiedades del espacio que se mantienen aunque se deforme continuamente. Él la llamó "geometría de posición" (Geometria Situs) y "análisis de posición" (Analysis Situs). Leibniz fue el primero en usar el término analysis situs, que luego se usaría en el siglo XIX para referirse a lo que hoy conocemos como topología.
Eponimia
Además de los distintos conceptos matemáticos que llevan su nombre, se tiene que:
- El cráter lunar Leibnitz lleva este nombre en su memoria.
- El asteroide (5149) Leibniz también conmemora su nombre.
Véase también
En inglés: Gottfried Wilhelm Leibniz Facts for Kids
- Notación de Leibniz
- Fórmula de Leibniz que es igual a Pi
- Calculus ratiocinator
- Regla de Leibniz
- La garra del león
- Serie de Leibniz
- Criterio de Leibniz
- Monadología
- Metafísica
- Vis viva
