Curva braquistócrona para niños
Una curva braquistócrona (del griego brachistos, 'el más corto', y chronos, 'tiempo') es el camino más rápido entre dos puntos para un objeto que se desliza por ella. Imagina que tienes dos puntos, uno más alto que el otro. Si dejas caer una canica desde el punto más alto, ¿qué forma de camino debería seguir para llegar al punto más bajo en el menor tiempo posible? Esa forma es la curva braquistócrona.
Este problema considera que el objeto empieza sin velocidad, se mueve solo por la fuerza de la gravedad y no hay fricción. Grandes científicos como Johann Bernoulli, Jakob Bernoulli, Gottfried Leibniz e Isaac Newton trabajaron para encontrar la solución a este fascinante desafío. Newton, por ejemplo, resolvió el problema el 24 de enero de 1697, lo que fue un paso importante en una rama de las matemáticas llamada cálculo de variaciones.
Contenido
Historia de la Curva Braquistócrona
¿Qué intentó Galileo?
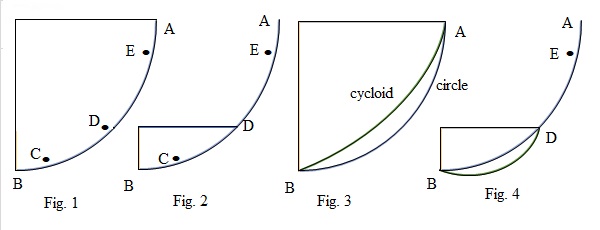
Mucho antes, en 1638, el famoso científico Galileo Galilei ya había pensado en un problema parecido. En su libro Dos nuevas ciencias, Galileo intentó descubrir el camino más rápido para que un objeto descendiera de un punto a otro. Él pensó que el arco de un círculo sería el camino más veloz.
Galileo creía que cuanto más se parecía un camino a un círculo, más rápido sería el descenso. Sin embargo, aunque Galileo estudió la curva llamada cicloide y le dio su nombre, no logró conectar esta curva con el problema del descenso más rápido. Esa conexión tuvo que esperar a que las matemáticas avanzaran más.
La idea de Galileo era que el tiempo más corto para que un objeto se moviera de un punto a otro sería siguiendo el arco de un cuarto de círculo. Él pensó que esto se aplicaba a cualquier parte de ese arco. Sin embargo, el verdadero camino más rápido, la braquistócrona, es en realidad una curva diferente, llamada cicloide.
El Desafío de Johann Bernoulli
En junio de 1696, el matemático Johann Bernoulli propuso el problema de la braquistócrona a otros científicos en una revista llamada Acta Eruditorum. Él quería desafiar a los matemáticos más brillantes del mundo.
Bernoulli planteó el problema así:
Dados dos puntos A y B en un plano vertical, ¿cuál es la curva que traza un punto sobre el que actúa únicamente la gravedad, que parte de A y llega a B en el menor tiempo?
Johann y su hermano Jakob Bernoulli encontraron la misma solución. Johann publicó la solución al año siguiente, señalando que la curva era la misma que la tautócrona de Huygens (otra curva especial).
Bernoulli dio un plazo para que se publicaran las soluciones. A petición de Gottfried Leibniz, el plazo se extendió. El 29 de enero de 1697, Isaac Newton recibió el desafío. Se dice que Newton se quedó despierto toda la noche para resolverlo y envió su solución de forma anónima. Cuando Johann Bernoulli vio la solución, inmediatamente supo que era de Newton, diciendo que "se reconoce al león por la marca de su garra". Esto muestra lo brillante que era Newton, ya que a Johann Bernoulli le había tomado dos semanas resolverlo.
Al final, cinco matemáticos presentaron soluciones: Newton, Jakob Bernoulli, Gottfried Leibniz, Ehrenfried Walther von Tschirnhaus y Guillaume de l'Hôpital. Las soluciones de cuatro de ellos se publicaron en la misma revista. Jakob Bernoulli, en un intento de superar a su hermano, desarrolló nuevos métodos para resolver una versión más difícil del problema. Estos métodos fueron mejorados por Leonhard Euler y se convirtieron en lo que hoy conocemos como cálculo de variaciones.
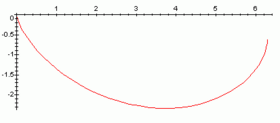
La Braquistócrona es una Cicloide
Si tienes dos puntos, A y B, y A está más alto que B, solo hay una curva cicloide que va de A a B con la forma correcta (cóncava hacia arriba) y que no tiene puntos más altos entre A y B. Esta cicloide invertida es la curva braquistócrona. Lo interesante es que la forma de esta curva no depende de cuánto pese el objeto ni del valor de la gravedad.
Este problema se puede resolver usando herramientas matemáticas avanzadas del cálculo variacional.
Es importante saber que si el objeto ya tiene una velocidad al principio, o si hay fricción (rozamiento), la curva que minimiza el tiempo de viaje será diferente a la cicloide simple.
¿Cómo se demuestra?
Para entender por qué la cicloide es la curva más rápida, los matemáticos usan principios de la física y las matemáticas. Uno de esos principios es la conservación de la energía, que nos dice cómo la velocidad de un objeto cambia a medida que cae debido a la gravedad.
La velocidad de un objeto que cae en un campo gravitatorio constante se puede calcular con una fórmula que depende de la altura desde la que ha caído. Luego, se usa otra fórmula para calcular el tiempo total que tarda el objeto en recorrer la curva. El objetivo es encontrar la forma de la curva que haga que este tiempo sea el más pequeño posible.
Al aplicar ciertas reglas matemáticas (llamadas ecuaciones de Euler-Lagrange), se llega a una ecuación que describe la forma de la curva. Resulta que la curva que satisface esta ecuación es precisamente la cicloide.
Propiedades Especiales
La curva braquistócrona también tiene otra propiedad asombrosa: es una curva tautócrona. Esto significa que si varios objetos empiezan a deslizarse al mismo tiempo desde diferentes puntos a lo largo de esta curva, todos llegarán al punto más bajo al mismo tiempo. ¡Es como si la curva los sincronizara!
Datos Curiosos
Según el principio de Fermat, la luz siempre viaja por el camino que le toma el menor tiempo. Si la velocidad de la luz aumentara de la misma manera que lo hace un objeto que cae por la gravedad, ¡la trayectoria de un rayo de luz sería una curva braquistócrona!
Variaciones del Problema
Con Rozamiento
El problema original de la braquistócrona asume que no hay fricción. Pero, ¿qué pasa si sí hay rozamiento? Los científicos también han resuelto este problema. En este caso, la curva más rápida sigue siendo una forma de cicloide, pero está ligeramente modificada para tener en cuenta la pérdida de energía debido a la fricción.
Movimiento en Superficies Curvas
Normalmente, el problema de la braquistócrona se plantea en un plano vertical. Sin embargo, también se ha estudiado y resuelto para situaciones en las que el objeto se mueve sobre una superficie curva, como un cono o una esfera. Esto hace que el problema sea aún más complejo e interesante.
Ver también
- Cálculo variacional
- Cicloide
- Curva tautócrona
- Catenaria
- Movimiento uniformemente acelerado
Véase también
 En inglés: Brachistochrone curve Facts for Kids
En inglés: Brachistochrone curve Facts for Kids