Eliminación de Gauss-Jordan para niños
La eliminación de Gauss-Jordan es un método matemático muy útil que nos ayuda a resolver problemas con varias ecuaciones y números desconocidos. Imagina que tienes un rompecabezas donde necesitas encontrar el valor de varias letras (como 'x', 'y', 'z') que cumplen con ciertas reglas al mismo tiempo. Este método, nombrado en honor a los matemáticos Carl Friedrich Gauss y Wilhelm Jordan, es como una guía paso a paso para encontrar esas soluciones.
También se usa para encontrar la "matriz inversa" de otra matriz. Una matriz es como una tabla de números organizada en filas y columnas. La matriz inversa es especial porque, al multiplicarla por la matriz original, el resultado es una matriz "identidad", que es como el número 1 en las multiplicaciones normales.
El método de Gauss-Jordan funciona transformando una tabla de números (matriz) mediante una serie de pasos sencillos. El objetivo es que la tabla quede de una forma muy ordenada, donde las soluciones sean fáciles de ver.
Contenido
- ¿Cómo funciona la eliminación de Gauss-Jordan?
- ¿De dónde viene este método?
- Pasos del algoritmo de eliminación de Gauss-Jordan
- Ejemplo práctico: Resolviendo un sistema de ecuaciones
- ¿Qué son las formas escalonada y escalonada reducida?
- Otras aplicaciones de la eliminación de Gauss-Jordan
- Véase también
¿Cómo funciona la eliminación de Gauss-Jordan?
Para resolver un sistema de ecuaciones o encontrar la inversa de una matriz, usamos unas "operaciones elementales" en las filas de la matriz. Piensa en estas operaciones como reglas que puedes aplicar a las filas sin cambiar las soluciones del problema.
Hay tres tipos de operaciones que puedes hacer:
- Intercambiar dos filas: Puedes cambiar el orden de dos filas completas.
- Multiplicar una fila por un número: Puedes multiplicar todos los números de una fila por un mismo número (que no sea cero).
- Sumar un múltiplo de una fila a otra: Puedes multiplicar una fila por un número y luego sumar el resultado a otra fila.
Usando estas operaciones, podemos transformar la matriz original en una forma especial llamada "forma escalonada reducida". En esta forma, los números principales de cada fila (el primer número diferente de cero) son 1, y todos los demás números en la misma columna de ese 1 son cero.
Por ejemplo, mira cómo una matriz se transforma paso a paso: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{bmatrix} 1 & 3 & 1 & 9 \\ 1 & 1 & -1 & 1 \\ 3 & 11 & 5 & 35 \end{bmatrix}\to \begin{bmatrix} 1 & 3 & 1 & 9 \\ 0 & -2 & -2 & -8 \\ 0 & 2 & 2 & 8 \end{bmatrix}\to \begin{bmatrix} 1 & 3 & 1 & 9 \\ 0 & -2 & -2 & -8 \\ 0 & 0 & 0 & 0 \end{bmatrix}\to \begin{bmatrix} 1 & 0 & -2 & -3 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & 0 & 0 \end{bmatrix}
El proceso de llegar a la forma escalonada reducida se llama eliminación de Gauss-Jordan. Si solo llegamos a una forma un poco menos ordenada, llamada "forma escalonada" (donde la matriz es triangular superior), se le llama eliminación de Gauss.
¿De dónde viene este método?
Algunas ideas parecidas a este método ya eran conocidas por los matemáticos en China hace mucho tiempo, alrededor del año 179 después de Cristo.
El método de eliminación de Gauss-Jordan aparece en un libro de matemáticas chino muy importante llamado Jiuzhang suanshu o Los nueve capítulos sobre el arte matemático. En este libro, se muestran ejemplos de cómo usarlo para resolver problemas con varias ecuaciones.
Pasos del algoritmo de eliminación de Gauss-Jordan
El proceso se puede dividir en dos partes principales:
Primera parte: Eliminación hacia adelante
Esta parte busca transformar la matriz en su "forma escalonada".
- Busca la primera columna de izquierda a derecha que no tenga solo ceros.
- Si el primer número de esa columna en la primera fila es cero, intercambia esa fila con otra que no tenga un cero en esa posición.
- Haz que todos los números debajo de ese primer número (llamado "pivote") en esa columna se conviertan en cero. Para lograrlo, sumas múltiplos adecuados de la fila del pivote a las filas de abajo.
- Ignora la fila y columna del pivote que acabas de usar y repite los pasos anteriores con la parte restante de la matriz.
Cuando terminas esta parte, la matriz está en forma escalonada. Desde aquí, ya puedes saber si el sistema tiene una solución única, infinitas soluciones o ninguna solución.
Segunda parte: Sustitución hacia atrás
Esta parte continúa el proceso para llegar a la "forma escalonada reducida".
- Empezando por la última fila que no es cero, haz que el primer número de esa fila (el pivote) sea 1. Para ello, puedes multiplicar toda la fila por el número necesario.
- Luego, haz que todos los números por encima de ese pivote se conviertan en cero, sumando múltiplos adecuados de la fila del pivote a las filas de arriba.
- Repite este proceso subiendo fila por fila hasta que todos los pivotes sean 1 y todos los números por encima y por debajo de ellos sean cero.
Ejemplo práctico: Resolviendo un sistema de ecuaciones
Imagina que queremos encontrar los valores de "x", "y" y "z" que cumplen estas tres ecuaciones al mismo tiempo:
Podemos representar este sistema con una matriz, que es una tabla de números. Los números de la izquierda son los que acompañan a las letras (coeficientes), y los de la derecha son los resultados:
Ahora, aplicamos las operaciones elementales para transformar esta matriz.
Paso 1: Hacemos ceros debajo del primer número (el 2 en la primera fila).
- Sumamos 3/2 veces la primera fila a la segunda fila.
- Sumamos la primera fila a la tercera fila.
La matriz se ve así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left [ \begin{array}{rrrr} 2 & 1 & -1 & 8 \\ 0 & 1/2 & 1/2 & 1 \\ 0 & 2 & 1 & 5 \end{array} \right ]
Paso 2: Hacemos ceros debajo del segundo número principal (el 1/2 en la segunda fila).
- Sumamos -4 veces la segunda fila a la tercera fila.
La matriz se ve así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left [ \begin{array}{rrrr} 2 & 1 & -1 & 8 \\ 0 & 1/2 & 1/2 & 1 \\ 0 & 0 & -1 & 1 \end{array} \right ]
Hasta aquí, si solo quisiéramos la eliminación de Gauss, podríamos resolver el sistema desde aquí. Pero para Gauss-Jordan, seguimos.
Paso 3: Ahora, trabajamos de abajo hacia arriba para hacer ceros por encima de los números principales.
- Multiplicamos la tercera fila por -1 para que el -1 se convierta en 1.
- Sumamos 1/2 veces la nueva tercera fila a la segunda fila.
- Sumamos -1 veces la nueva tercera fila a la primera fila.
La matriz se ve así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left [ \begin{array}{rrrr} 2 & 1 & 0 & 7 \\ 0 & 1/2 & 0 & 3/2 \\ 0 & 0 & 1 & -1 \end{array} \right ]
Paso 4: Hacemos ceros por encima del segundo número principal (el 1/2 en la segunda fila).
- Multiplicamos la segunda fila por 2 para que el 1/2 se convierta en 1.
- Sumamos -1 veces la nueva segunda fila a la primera fila.
La matriz final se ve así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left [ \begin{array}{rrrr} 2 & 0 & 0 & 4 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & -1 \end{array} \right ]
Paso 5: Finalmente, dividimos la primera fila por 2 para que el primer número principal sea 1.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left [ \begin{array}{rrrr} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & -1 \end{array} \right ]
¡Listo! La matriz está en su forma escalonada reducida. Esto significa que las soluciones son:
- x = 2
- y = 3
- z = -1
Si en algún momento, al hacer las operaciones, obtienes una fila como `[0 0 0 | a]` donde 'a' es un número diferente de cero, significa que el sistema no tiene solución. Es como decir "0 = 5", lo cual es imposible. Si 'a' fuera cero, significaría que hay infinitas soluciones.
¿Qué son las formas escalonada y escalonada reducida?
Estas son dos formas especiales en las que podemos organizar una matriz:
- Forma escalonada: Una matriz está en forma escalonada si cumple estas reglas:
* Todas las filas que solo tienen ceros están al final de la matriz. * El primer número diferente de cero en cada fila (llamado "pivote") está más a la derecha que el pivote de la fila de arriba. * Todos los números debajo de un pivote son cero.
- Forma escalonada reducida: Una matriz está en forma escalonada reducida si, además de las reglas anteriores, cumple estas otras:
* Todos los pivotes son iguales a 1. * Todos los números por encima de los pivotes también son cero.
Cuando una matriz de un sistema de ecuaciones está en forma escalonada reducida, es muy fácil saber cuántas soluciones tiene:
- Si aparece un pivote en la columna de los resultados (la última columna), el sistema no tiene solución.
- Si no hay pivotes en la columna de los resultados, el sistema sí tiene solución.
* Si el número de pivotes es igual al número de incógnitas (letras), el sistema tiene una única solución. * Si el número de pivotes es menor que el número de incógnitas, el sistema tiene infinitas soluciones.
Otras aplicaciones de la eliminación de Gauss-Jordan
Encontrar la inversa de una matriz
La eliminación de Gauss-Jordan también se puede usar para encontrar la matriz inversa de una matriz cuadrada (que tiene el mismo número de filas y columnas).
Para hacer esto, se coloca la matriz original junto a una "matriz identidad" (una matriz especial con unos en la diagonal y ceros en el resto). Por ejemplo, si tenemos la matriz A:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A= \left [ \begin{array}{rrr} 2 & 1 & -1 \\ -3 & -1 & 2 \\ -2 & 1 & 2 \end{array} \right ]
La combinamos con la matriz identidad así:
Luego, aplicamos las operaciones elementales de fila a toda esta matriz combinada, hasta que la parte izquierda (donde estaba la matriz A) se convierta en la matriz identidad. Cuando eso sucede, la parte derecha (donde estaba la matriz identidad) se habrá transformado en la matriz inversa de A.
Por ejemplo, siguiendo los pasos de eliminación de Gauss-Jordan, la matriz anterior se transformaría en:
Esto significa que la matriz inversa de A es la matriz de la derecha. Si la parte izquierda no se convierte en la matriz identidad, entonces la matriz original no tiene inversa.
Véase también
 En inglés: Gaussian elimination Facts for Kids
En inglés: Gaussian elimination Facts for Kids


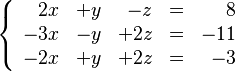
![\left [
\begin{array}{rrrr}
2 & 1 & -1 & 8 \\
-3 & -1 & 2 & -11 \\
-2 & 1 & 2 & -3
\end{array}
\right ]](/images/math/b/7/5/b75b0e02a527cf69e6f42dbd2fe2960f.png)
![\left [ \begin{array}{rrr|rrr}
2 & 1 & -1 & 1 & 0 & 0 \\
-3 & -1 & 2 & 0 & 1 & 0 \\
-2 & 1 & 2 & 0 & 0 & 1
\end{array} \right ]](/images/math/9/e/a/9eacbd40cfec5f75f6738cab4ab63fdb.png)
![\left [ \begin{array}{ccc|ccc}
1 & 0 & 0 &\,\,\,\, 4 & \,\,\,\, 3 & -1 \\
0 & 1 & 0 & -2 & -2 &\,\,\,\, 1 \\
0 & 0 & 1 & \,\,\,\, 5 & \,\,\,\, 4 & -1
\end{array} \right ]](/images/math/2/5/f/25fc3e620c741de3675609c779c1d3c8.png)