Lógica matemática para niños

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada. Busca fuentes: «Lógica matemática» – noticias · libros · acad%C3%A9mico · im%C3%A1genes Este aviso fue puesto el 19 de abril de 2024.

En matemática, teoría de modelos es el estudio de (clases de) estructuras matemáticas tales como grupos, cuerpos, grafos, o incluso universos de teoría de conjuntos, en relación con las teorías axiomáticas y la lógica matemática. La teoría de modelos permite atribuir una interpretación semántica a las expresiones puramente formales de los lenguajes formales. Además permite estudiar en sí mismos los conjuntos de axiomas, su completitud, consistencia, independencia mutua, y permiten introducir un importante número de cuestiones metalógicas.

Al mismo tiempo los lenguajes en los que se ha estructurado la noción de verdad y de los que habla la teoría de modelos son, por lo general, sistemas matemáticos. Las «cosas» representadas en dichos lenguajes son también sistemas matemáticos. Por esto, la teoría de modelos es una teoría semántica que pone en relación unos sistemas matemáticos con otros sistemas matemáticos. Dicha teoría nos proporciona algunas pistas con respecto a aquella semántica que pone en relación los lenguajes naturales con la realidad. Sin embargo, ha de tenerse siempre presente que no hay ningún sustituto matemático para los problemas genuinamente filosóficos. Y el problema de la verdad es un problema netamente filosófico.

Padilla Gálvez, Jesús Padilla Gálvez (2007). Verdad y demostración. Plaza y Valdés. p. 229. ISBN 9788496780194. OCLC 427520428. Consultado el 28 de febrero de 2019. 

VEB Robotron Elektronik Dresden.

La teoría de la computabilidad o teoría de la recursión es la parte de la computación que estudia los problemas de decisión que se pueden resolver con un algoritmo o equivalentemente con una máquina de Turing. Las preguntas fundamentales de la teoría de la computabilidad son:

• ¿Qué problemas puede resolver una máquina de Turing?
• ¿Qué otros formalismos equivalen a las máquinas de Turing?
• ¿Qué problemas requieren máquinas más poderosas?
• ¿Qué problemas requieren máquinas menos poderosas?

La teoría de la complejidad computacional clasifica las funciones computables según el uso que hacen de diversos recursos en diversos tipos de máquina.

Un diagrama de Venn que ilustra la intersección de dos conjuntos.

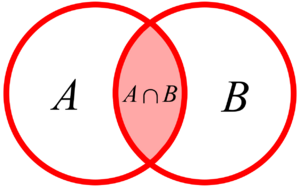
La teoría de conjuntos es una rama de la lógica matemática que estudia las propiedades y relaciones de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una herramienta básica que permite formular de cualquier otra teoría matemática.

La teoría de los conjuntos es lo suficientemente flexible y general para construir el resto de objetos y estructuras de interés en matemáticas: números, funciones, figuras geométricas, etc; gracias a las herramientas de la lógica, permite estudiar los fundamentos.

Además, la propia teoría de conjuntos es objeto de estudio per se, no solo como herramienta auxiliar, en particular las propiedades y relaciones de los conjuntos infinitos. En esta disciplina es habitual que se presenten casos de propiedades indemostrables o contradictorias, como la hipótesis del continuo o la existencia de algún cardinal inaccesible. Por esta razón, sus razonamientos y técnicas se apoyan en gran medida en la lógica matemática.

El desarrollo histórico de la teoría de conjuntos se atribuye a Georg Cantor, que comenzó a investigar cuestiones conjuntistas (puras) del infinito en la segunda mitad del siglo XIX, precedido por algunas ideas de Bernhard Bolzano e influido por Richard Dedekind. El descubrimiento de las paradojas de la teoría cantoriana de conjuntos, formalizada por Gottlob Frege, propició los trabajos de Bertrand Russell, Ernst Zermelo y Abraham Fraenkel.

La teoría de conjuntos se emplea habitualmente como sistema fundacional de toda la matemática, en particular en la forma de la teoría de conjuntos de Zermelo-Fraenkel con el axioma de elección. Además de su papel fundacional, la teoría de conjuntos también proporciona el marco para desarrollar una teoría matemática del infinito, y tiene varias aplicaciones en informática, filosofía y semántica formal. Su atractivo fundacional, junto con sus paradojas, sus implicaciones para el concepto de infinito y sus múltiples aplicaciones han hecho de la teoría de conjuntos un área de gran interés para lógicos y filósofos de la matemática. La investigación contemporánea sobre la teoría de conjuntos abarca una amplia gama de temas, que van desde la estructura de la línea de números reales hasta el estudio de la consistencia del cardinal grande.

La teoría de la demostración o teoría de la prueba es una rama de la lógica matemática que trata a las demostraciones como objetos matemáticos, facilitando su análisis mediante técnicas matemáticas. Las demostraciones suelen presentarse como estructuras de datos inductivamente definidas que se construyen de acuerdo con los axiomas y reglas de inferencia de los sistemas lógicos. En este sentido, la teoría de la demostración se ocupa de la sintaxis, en contraste con la teoría de modelos, que trata con la semántica. Junto con la teoría de modelos, la teoría de conjuntos axiomática y la teoría de la computabilidad, la teoría de la demostración es uno de los «cuatro pilares» de los fundamentos de las matemáticas.

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada. Busca fuentes: «Lógica matemática» – noticias · libros · acad%C3%A9mico · im%C3%A1genes Este aviso fue puesto el 19 de abril de 2024.

Un sistema formal o sistema lógico es un sistema abstracto compuesto por un lenguaje formal, axiomas, reglas de inferencia y a veces una semántica formal, que se utiliza para deducir o demostrar teoremas y dar una definición rigurosa del concepto de demostración. Un sistema formal es una formalización rigurosa y completa del concepto de sistema axiomático, los cuales se pueden expresar en lenguaje formal o en lenguaje natural formalizado. Al crear un sistema formal se pretende capturar y abstraer la esencia de determinadas características del mundo real, en un modelo conceptual expresado en un determinado lenguaje formal. Algunos de los sistemas formales más conocidos son la lógica proposicional, la lógica de primer orden y la lógica modal.

En la teoría de la demostración, las demostraciones formales se pueden expresar en el lenguaje de los sistemas formales, consistentes en axiomas y reglas de inferencia. Los teoremas pueden ser obtenidos por medio de demostraciones formales. Este punto de vista de las matemáticas ha sido denominado formalista; aunque en muchas ocasiones este término conlleva una acepción peyorativa. En ese sentido, David Hilbert creó la metamatemática para estudiar los sistemas formales, entendiendo que el lenguaje utilizado para ello, denominado metalenguaje era distinto del lenguaje del sistema formal que se pretendía estudiar, al que se llama lenguaje objeto.

Un sistema así es la reducción de un lenguaje formalizado a meros símbolos, lenguaje formalizado y simbolizado sin contenido material alguno; un lenguaje reducido a mera forma que se expresa mediante fórmulas que reflejan las relaciones sintácticas entre los símbolos y las reglas de formación y transformación que permiten construir las fórmulas del sistema y pasar de una fórmula a otra.

Una teoría axiomática es un conjunto de fórmulas en un determinado lenguaje formal y todas las fórmulas deducibles de dichas expresiones mediante las reglas de inferencia posibles en dicho sistema formal. El objetivo de las teorías axiomáticas es construir sistemas formales que representen las características esenciales de ramas enteras de las matemáticas. Si se selecciona un conjunto más amplio o menos amplio de axiomas el conjunto de teoremas deducibles cambian. El interés de la teoría de modelos es que en un modelo en que satisfagan los axiomas de determinada teoría también se satisfacen los teoremas deducibles de dicha teoría. Es decir, si un teorema es deducible en una cierta teoría, entonces ese teorema es universalmente válido en todos los modelos que satisfacen los axiomas. Esto es interesante porque en principio la clase de modelos que satisface una cierta teoría es difícil de conocer, ya que las teorías matemáticas interesantes en general admiten toda clase infinita de modelos no isomorfos, por lo que su clasificación en general resulta difícilmente abordable si no existe un sistema formal y un conjunto de axiomas que caracterice los diferentes tipos de modelos.

En el siglo XX, Hilbert y otros sostuvieron que la matemática es un sistema formal. Pero en 1931, Kurt Gödel demostró que ningún sistema formal con suficiente poder expresivo para capturar la aritmética de Peano puede ser a la vez consistente y completo. El teorema de la incompletitud de Gödel, junto con la demostración de Alonzo Church de que la matemática tampoco es decidible, terminó con el programa de Hilbert. Sin embargo, a pesar de sus limitaciones, el enfoque sigue siendo ampliamente usado, básicamente porque no se ha encontrado ninguna alternativa mejor al enfoque formalista de Hilbert y la pretensión de trabajar en el seno de teorías matemáticas explícitamente axiomatizadas, aun con sus limitaciones.

Los sistemas formales también han encontrado aplicación dentro de la informática, la teoría de la información y la estadística.

La metalógica es la rama de la lógica que estudia las propiedades y los componentes de los sistemas formales. Las propiedades más importantes que se pueden demostrar de los sistemas formales son la consistencia, decidibilidad y completitud. Ejemplos de teoremas metalógicos importantes son los teoremas de incompletitud de Gödel, el teorema de completitud de Gödel y el teorema de Löwenheim-Skolem. Otra propiedad es la compacidad.