Función convexa para niños

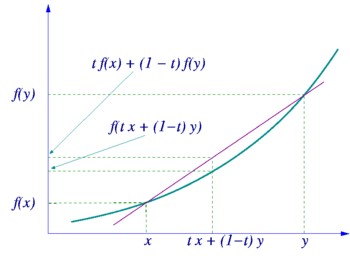
Una función convexa en matemática es un tipo especial de función que tiene una forma particular. Imagina que tienes el dibujo de una función en una gráfica. Si tomas dos puntos cualquiera en esa gráfica y los unes con una línea recta (como una cuerda), esa línea siempre quedará por encima o tocando la función.

Piensa en la forma de una taza o un cuenco que está hacia arriba. Esa es la forma de una función convexa. Si la taza estuviera boca abajo, sería una función cóncava.

¿Qué es una función convexa?

Una función convexa en un intervalo [x,y]. La línea recta (cuerda) entre dos puntos siempre está por encima de la función.

Una función matemática f se considera convexa si cumple una condición especial. Imagina que tienes un dibujo de la función. Si eliges dos puntos cualquiera en ese dibujo y los unes con una línea recta, esa línea siempre debe estar por encima o justo sobre la curva de la función.

Esto significa que la función tiene una forma que se "curva hacia arriba".

• Una función estrictamente convexa es aún más "curva hacia arriba". En este caso, la línea recta que une dos puntos siempre estará estrictamente por encima de la función, nunca la tocará en el medio.

• Una función es cóncava si es lo contrario de convexa. Es como un cuenco boca abajo. Si la función f es cóncava, entonces la función -f (que es la misma función pero reflejada hacia arriba) es convexa.

Características de las funciones convexas

Una función (en azul) es convexa si la región sobre su gráfica (en verde) es un conjunto convexo.

Las funciones convexas tienen algunas características interesantes:

• Son generalmente "suaves" o "continuas" en la mayoría de sus puntos. Esto significa que puedes dibujar la función sin levantar el lápiz.
• Si una función es convexa, cualquier punto donde la función alcanza su valor más bajo (un mínimo local) es también el valor más bajo de toda la función (un mínimo absoluto). Piensa en el fondo de un cuenco: es el punto más bajo de todo el cuenco.
• Si una función es estrictamente convexa, solo tendrá un único punto donde alcanza su valor más bajo.

¿Cómo saber si una función es convexa?

Para las funciones que se pueden "derivar" (es decir, podemos calcular su tasa de cambio o pendiente):

• Si la "pendiente" de la función (su primera derivada) siempre va aumentando o se mantiene igual, entonces la función es convexa.
• Si la "curvatura" de la función (su segunda derivada) es siempre positiva o cero, entonces la función es convexa. Esto es una forma muy útil de comprobarlo. Si la segunda derivada es positiva, la función es estrictamente convexa.

Ejemplos de funciones convexas

Aquí tienes algunos ejemplos para entender mejor:

• La función f(x) = x² (equis al cuadrado) es convexa. Si la dibujas, verás que tiene forma de "U" hacia arriba. Su segunda derivada es 2, que es siempre positiva.
• La función f(x) = |x| (valor absoluto de equis) también es convexa. Su gráfica forma una "V" que apunta hacia abajo. Aunque no tiene una pendiente definida en el punto x=0, sigue siendo convexa.
• La función f(x) = x³ (equis al cubo) es un poco diferente. Es convexa cuando x es mayor o igual a 0, y cóncava cuando x es menor o igual a 0.
• Cualquier línea recta, como f(x) = 2x + 3, es tanto convexa como cóncava al mismo tiempo. Esto es porque la "cuerda" que une dos puntos siempre está exactamente sobre la línea.

Teoremas importantes sobre funciones convexas

Los matemáticos han descubierto reglas y teoremas sobre las funciones convexas que son muy útiles:

• Mínimos de funciones convexas: Si una función es convexa, cualquier punto donde la función alcanza un valor mínimo en una pequeña parte de su gráfica (mínimo local) es en realidad el valor mínimo más bajo de toda la función (mínimo absoluto). Si la función es estrictamente convexa, solo puede tener un único punto mínimo.

• Relación con la pendiente: Una función es convexa si y solo si su gráfica siempre está por encima de todas sus líneas tangentes (líneas que tocan la curva en un solo punto).

• Relación con la curvatura: Si una función se puede derivar dos veces, es convexa si y solo si su "curvatura" (segunda derivada) es siempre mayor o igual a cero.

Galería de imágenes

• 

  Función convexa

Ver también

• Función real de variable real
• Convexidad
• Polígono convexo
• Función cóncava

Véase también

En inglés: Convex function Facts for Kids