Función exponencial para niños
Datos para niños Funciones exponenciales |
||
|---|---|---|
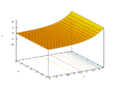
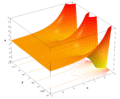
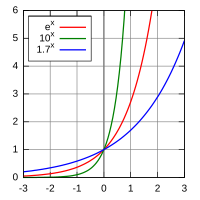 Gráfica de Funciones exponenciales
|
||
| Definición |  |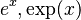
|
| Tipo | Función real | |
| Dominio |  |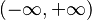
|
| Codominio |  |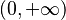
|
| Imagen | |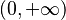
|
| Propiedades | Biyectiva Convexa Estrictamente creciente Trascendente |
|
| Cálculo infinitesimal | ||
| Derivada |  |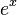
|
| Función primitiva | |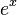
|
| Función inversa |  |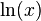
|
| Límites |   |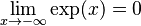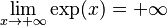
|
| Funciones relacionadas | Logaritmo | |
En matemáticas, una función exponencial es un tipo especial de función donde la variable (generalmente x) se encuentra en el exponente. Su forma más común es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = ab^x . Esto significa que la base b se eleva a la potencia de x, y luego se multiplica por un número a.
La función exponencial es muy importante porque describe situaciones donde una cantidad crece o disminuye a un ritmo que depende de su tamaño actual. Por ejemplo, el crecimiento de una población o el interés que ganas en una cuenta de ahorros.
Existe una función exponencial muy especial llamada la "función exponencial natural". Se escribe como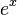 
o 
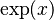. Aquí, la base es un número irracional llamado e, que es aproximadamente 2.71828. Este número e es único porque la forma en que la función crece es exactamente igual a su propio valor.
La función exponencial natural tiene una propiedad fundamental: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{x+y} = e^x e^y . Esto significa que si sumas los exponentes, puedes multiplicar los resultados de la función.
Contenido
¿Qué es una Función Exponencial?
Una función exponencial es aquella donde la variable está en el exponente. Por ejemplo, en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = 2^x , si x es 1, el resultado es 2; si x es 2, el resultado es 4; si x es 3, el resultado es 8. ¡El número crece muy rápido!
El Número e y su Importancia
El número e es una constante matemática muy especial, como π. Su valor es aproximadamente 2.71828. La función exponencial con base e (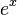) es única porque su tasa de cambio (qué tan rápido sube o baja) es igual a su propio valor. Esto la hace muy útil en muchas áreas de la ciencia.
Por ejemplo, si tienes una cantidad que se duplica cada cierto tiempo, eso es crecimiento exponencial. Si se reduce a la mitad, es decaimiento exponencial. La función 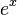es la forma más sencilla de describir este tipo de cambios.
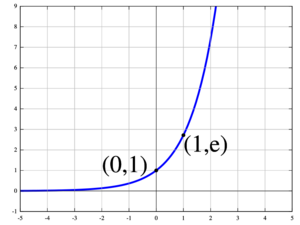
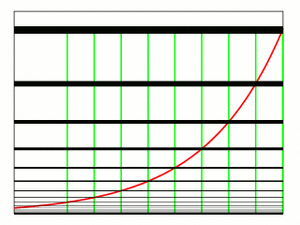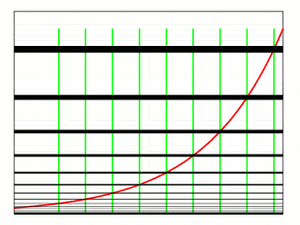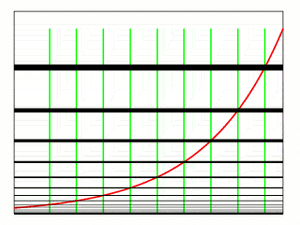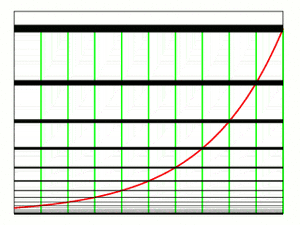
¿Cómo se ve la Gráfica de una Función Exponencial?
La gráfica de 
siempre sube y lo hace cada vez más rápido a medida que x aumenta. La curva siempre está por encima del eje x (nunca lo toca ni lo cruza), pero puede acercarse mucho a él cuando x es un número negativo grande.
La función inversa de la función exponencial es el logaritmo natural, que se escribe com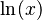o 
o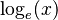 
. Son como operaciones opuestas, igual que sumar y restar, o multiplicar y dividir.
¿Para qué se usan las Funciones Exponenciales?
Las funciones exponenciales aparecen en muchos lugares en las matemáticas y en la vida real.
Crecimiento y Decaimiento
Las funciones exponenciales se usan para modelar situaciones donde algo crece o disminuye a una velocidad que depende de su tamaño actual. Algunos ejemplos son:
- El interés compuesto en una cuenta de ahorros: el dinero crece porque los intereses también generan intereses.
- El crecimiento de poblaciones de animales o bacterias.
- El decaimiento de materiales radiactivos (cómo se van desintegrando con el tiempo).
Definición por Series
Una forma de entender la función exponencial es a través de una suma infinita de términos, llamada serie de potencias: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \exp(x) = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + \cdots Cuantos más términos sumes, más cerca estarás del valor real de .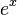
Definición por Límites
Otra forma de definir 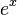es usando un límite: 
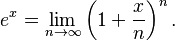Esto significa que si tomas un número muy grande para n, el resultado de la expresión se acercará mucho a 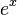. Esta definición se relaciona con el cálculo del interés compuesto.
Propiedades Especiales
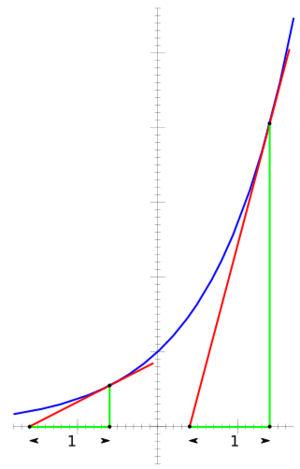
Una de las propiedades más importantes de la función exponencial 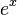es que su tasa de cambio (su derivada) es igual a la función misma. Esto significa que la pendiente de la gráfica en cualquier punto es igual a la altura de la función en ese punto.
Esto es muy útil para resolver problemas donde la velocidad de cambio de algo es proporcional a la cantidad que ya existe. Por ejemplo, si una población crece a una velocidad que depende de cuántos individuos hay, se puede usar una función exponencial para predecir su tamaño futuro.
Galería de imágenes
-
La parte real de la función exponencial compleja.
-
La parte imaginaria de la función exponencial compleja.
-
El módulo (tamaño) de la función exponencial compleja.
-
Clave de colores para el dominio de la función exponencial compleja.
-
Proyección de la función exponencial compleja en el plano de rango.
-
Proyección de la función exponencial compleja en 3D, mostrando una forma de embudo.
-
Proyección de la función exponencial compleja en 3D, mostrando una forma espiral.
-
Gráfico de la parte real de una función exponencial en el campo de los números complejos.
.png)
Véase también
En inglés: Exponential function Facts for Kids
- Número e
- Logaritmo natural
- Exponenciación
|
