Derivada para niños
En el cálculo diferencial, la derivada de una función nos dice qué tan rápido cambia el valor de esa función en un momento específico. Imagina que tienes una función que describe cómo se mueve algo; su derivada te dirá la velocidad de ese objeto en cada instante.
Piensa en un avión que vuela. Si sabes que recorrió 4500 km en 6 horas, puedes calcular su velocidad media (750 km/h). Pero el avión no siempre vuela a la misma velocidad. A veces va más rápido, a veces más lento. La derivada nos permite saber la velocidad instantánea del avión en un momento exacto, por ejemplo, a las 3:20 de la tarde. Para calcularla, se mira la velocidad media en intervalos de tiempo cada vez más pequeños alrededor de ese momento.
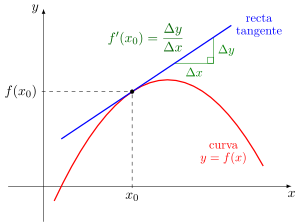
Desde el punto de vista de un dibujo (una gráfica de la función), la derivada en un punto es como la inclinación de la línea que toca la curva de la función justo en ese punto. Esa línea se llama recta tangente.
Contenido
Historia de la derivada
La idea de entender cómo cambian las cosas rápidamente ha existido desde la antigua Grecia. Sin embargo, los métodos para calcular esto de forma sistemática no aparecieron hasta el siglo XVII.
Los matemáticos Isaac Newton y Gottfried Leibniz son considerados los creadores del cálculo diferencial e integral. Ellos desarrollaron las reglas que usamos hoy para encontrar derivadas. Newton pensó en la derivada como la velocidad con la que algo "fluye" o cambia con el tiempo. Leibniz, por su parte, la vio más como la inclinación de una línea que toca una curva.
Leibniz también inventó muchos de los símbolos matemáticos que usamos, como el símbolo de la derivada 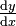 .
.
¿Para qué sirve la derivada?
La derivada es una herramienta muy importante en las matemáticas. Nos ayuda a medir la rapidez con la que cambia algo. Por eso, se usa mucho en:
- Física: Para calcular velocidades, aceleraciones y cómo se mueven los objetos.
- Química: Para entender la velocidad de las reacciones.
- Biología: Para estudiar el crecimiento de poblaciones o la propagación de enfermedades.
- Economía: Para analizar cómo cambian los precios o las ganancias.
En un gráfico, la derivada nos ayuda a saber si una función está subiendo o bajando (si es creciente o decreciente) y cómo se curva (si es cóncava o convexa).
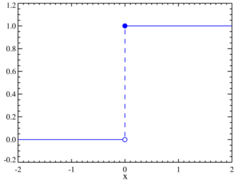
Algunas funciones no tienen derivada en todos sus puntos. Por ejemplo, si la gráfica de una función tiene una "esquina" o un "salto", no se puede dibujar una línea tangente clara en ese punto. Por suerte, la mayoría de las funciones que usamos en la vida real son "suaves" y sí se pueden derivar.
¿Cómo se calcula la derivada?
Para entender la derivada de una función  en un punto
en un punto  , imaginemos una línea que pasa por ese punto
, imaginemos una línea que pasa por ese punto 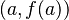 y por otro punto muy cercano
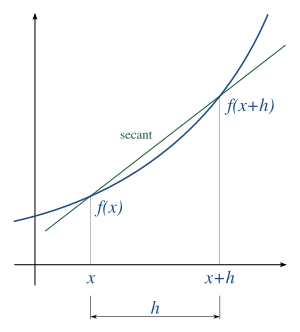
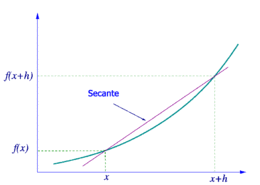
y por otro punto muy cercano 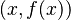 . La inclinación de esta línea se calcula con una fórmula llamada "cociente diferencial".
. La inclinación de esta línea se calcula con una fórmula llamada "cociente diferencial".
Cuanto más cerca esté el segundo punto del primero, más se parecerá la inclinación de esa línea a la inclinación de la línea tangente en el punto  . La derivada es el resultado de hacer que esa distancia entre los puntos sea casi cero.
. La derivada es el resultado de hacer que esa distancia entre los puntos sea casi cero.
Por ejemplo, si tenemos la función 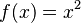 , su derivada es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(x)=2x . Esto significa que la inclinación de la línea tangente a la curva
, su derivada es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(x)=2x . Esto significa que la inclinación de la línea tangente a la curva 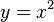 en cualquier punto
en cualquier punto  es
es 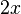 .
.
¿Qué es la continuidad y la derivabilidad?
Para que una función tenga derivada en un punto, primero debe ser continua en ese punto. Esto significa que su gráfica no debe tener "saltos" o "huecos". Si la gráfica está "rota", no hay una forma clara de dibujar una línea tangente.
Sin embargo, ser continua no es suficiente para tener derivada. Una función puede ser continua pero no derivable si su gráfica tiene una "esquina" o un "pico".
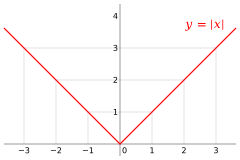
Un ejemplo es la función valor absoluto 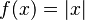 . Esta función es continua en
. Esta función es continua en 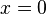 (no tiene saltos), pero su gráfica tiene una esquina afilada en ese punto. Por eso, no se puede dibujar una única línea tangente, y la función no tiene derivada en
(no tiene saltos), pero su gráfica tiene una esquina afilada en ese punto. Por eso, no se puede dibujar una única línea tangente, y la función no tiene derivada en 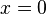 .
.
Formas de escribir la derivada
Existen varias maneras de escribir la derivada de una función:
Notación de Lagrange
Esta es la más común. Si tienes una función  , su derivada se escribe como
, su derivada se escribe como 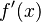 . Se lee "f prima de x". Si necesitas la derivada de la derivada (la segunda derivada), se escribe
. Se lee "f prima de x". Si necesitas la derivada de la derivada (la segunda derivada), se escribe 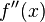 , y así sucesivamente.
, y así sucesivamente.
Notación de Leibniz
Esta notación es muy útil porque muestra qué variable se está usando para derivar. Se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{d(f(x))}{dx} o 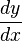 si
si 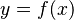 . Se lee "derivada de y con respecto a x".
. Se lee "derivada de y con respecto a x".
Notación de Newton
Newton usaba un punto encima de la letra para indicar la derivada, especialmente cuando se derivaba con respecto al tiempo. Por ejemplo, 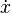 significa la derivada de
significa la derivada de  con respecto al tiempo. Esta notación se usa mucho en física para la velocidad y la aceleración.
con respecto al tiempo. Esta notación se usa mucho en física para la velocidad y la aceleración.
Notación de Euler
Se usa Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathrm D_x f o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \partial_x f . Aquí, D o ∂ son como "operadores" que indican que se está derivando.
Reglas para calcular derivadas
Calcular derivadas directamente con la definición puede ser complicado. Por suerte, existen reglas que nos facilitan el trabajo:
- Regla de la constante: Si una función es un número fijo (una constante), su derivada es 0. Por ejemplo, la derivada de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x)=7 es
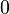 .
. - Regla de la suma: La derivada de una suma de funciones es la suma de sus derivadas.
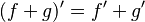 .
. - Regla del producto: Si tienes dos funciones multiplicándose, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (fg)' = f'g + fg' .
- Regla del cociente: Si tienes una función dividida por otra,
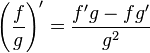 .
. - Regla de la cadena: Esta es para funciones "anidadas" (una función dentro de otra). Si
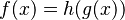 , entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(x) = h'(g(x)) \cdot g'(x) .
, entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(x) = h'(g(x)) \cdot g'(x) .
Ejemplo de cálculo
Vamos a derivar la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = x^4 + \sen (x^2) - \ln(x) e^x + 7 . Usando las reglas, la derivada es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(x) = 4x^3 + 2x\cos (x^2) - \frac{1}{x} e^x - \ln(x) e^x. Aquí usamos la regla de la cadena para Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen(x^2) y la regla del producto para Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ln(x) e^x .
Derivadas de funciones comunes
Aquí tienes una tabla con las derivadas de algunas funciones básicas:
Función  |
Derivada 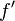 |
|
|---|---|---|
| Función potencia | Función constante 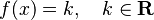 |
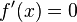 |
Función identidad 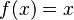 |
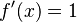 |
|
| Multiplicación por una constante: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x)=k \cdot g(x),\quad k\in\mathbf R | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(x)=k \cdot g'(x) | |
Potencia de exponente natural: 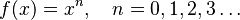 |
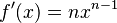 |
|
Función raíz cuadrada 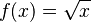 |
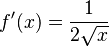 |
|
Función recíproca 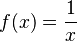 |
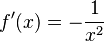 |
|
Caso general: 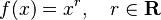 |
 |
|
| Función exponencial | Base  : : 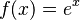 |
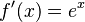 |
Caso general: 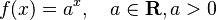 |
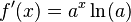 |
|
| Función logarítmica | Logaritmo en base  : : 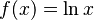 |
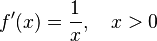 |
Caso general: 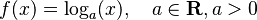 |
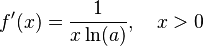 |
|
| Funciones trigonométricas | Función seno: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = \sen(x) | 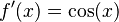 |
Función coseno: 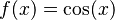 |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(x) = -\sen(x) | |
Función tangente: 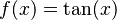 |
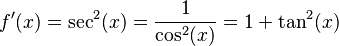 |
|
| Funciones trigonométricas inversas | Función arcoseno: 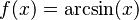 |
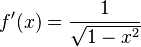 |
Función arcocoseno: 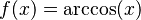 |
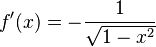 |
|
Función arcotangente: 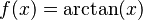 |
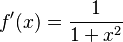 |
|
| Funciones hiperbólicas | Función seno hiperbólico: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = \sinh(x) | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(x) = \cosh(x) |
| Función coseno hiperbólico: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = \cosh(x) | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(x) = \sinh(x) | |
| Función tangente hiperbólica: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = \tanh(x) | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(x) = \mathrm{sech}^2(x) = \frac{1}{\mathrm{cosh}^2(x)} | |
Véase también
 En inglés: Derivative Facts for Kids
En inglés: Derivative Facts for Kids
- Reglas de derivación
- Tabla de derivadas
- Integral