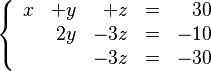Sistema de ecuaciones lineales para niños

Enciclopedia para niños

Un sistema de ecuaciones lineales es un conjunto de ecuaciones donde cada una es de "primer grado". Esto significa que las variables (las letras que representan números desconocidos, como x, y, z) no tienen exponentes (como x²) ni están multiplicándose entre sí (como xy).

Imagina que tienes un rompecabezas con varias pistas, y cada pista es una ecuación. Tu objetivo es encontrar los números que hacen que todas las pistas sean ciertas al mismo tiempo.

Aquí tienes un ejemplo de un sistema de ecuaciones lineales:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left \{ \begin{array}{rcrcrcr} 3 \,x_1 & + & 2\,x_2 & + & \,x_3 & = & 1 \\ 2 \,x_1 & + & 2\,x_2 & + & 4 \,x_3 & = & -2 \\ - \,x_1 & + & \frac{1}{2} \,x_2 & - & \,x_3 & = & 7 \end{array} \right .

El desafío es descubrir los valores de x₁, x₂ y x₃ que hacen que las tres ecuaciones sean correctas.

Los sistemas de ecuaciones lineales son muy importantes en matemáticas y se usan en muchísimas áreas. Por ejemplo, ayudan a resolver problemas en ingeniería, a entender cómo se mueven las cosas, a planificar proyectos y a predecir resultados en diferentes campos. Son una herramienta fundamental para los científicos y los ingenieros.

Contenido

¿Cómo se ven los sistemas de ecuaciones lineales?
¿Cómo se representan los sistemas lineales?
- Representación gráfica de sistemas lineales
¿Qué tipos de sistemas lineales existen?
¿Cómo se resuelven los sistemas de ecuaciones lineales?
Galería de imágenes
Véase también

¿Cómo se ven los sistemas de ecuaciones lineales?

Un sistema de ecuaciones lineales puede tener muchas ecuaciones y muchas variables desconocidas. Para que sea más fácil de entender, los matemáticos usan una forma general para escribirlos.

Imagina que tienes m ecuaciones (filas) y n incógnitas (columnas). Se vería algo así:

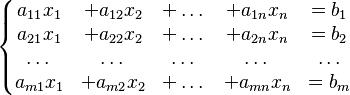
$\left \{ \begin{matrix} a_{11}x_1 & + a_{12}x_2 & + \dots & + a_{1n}x_n & = b_1 \\ a_{21}x_1 & + a_{22}x_2 & + \dots & + a_{2n}x_n & = b_2 \\ \dots & \dots & \dots & \dots & \dots \\ a_{m1}x_1 & + a_{m2}x_2 & + \dots & + a_{mn}x_n & = b_m \end{matrix} \right .$

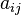Aquí, $x_1,\dots,x_n$ son las variables que queremos encontrar. Los números $a_{ij}$ son los "coeficientes", que son los números que multiplican a las variables. Y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b_1,\dots,b_m son los "términos independientes", que son los números que están solos al otro lado del signo igual.

Los matemáticos a menudo usan matrices para escribir estos sistemas de forma más compacta. Una matriz es como una tabla de números. Así, el sistema se puede representar como:

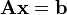
$\mathbf{Ax} = \mathbf{b}$

Donde A es la matriz de los coeficientes, x es un vector (una lista) de las variables, y b es un vector de los términos independientes.

¿Cómo se representan los sistemas lineales?

Cuando trabajamos con sistemas de ecuaciones lineales que tienen números reales (los que usamos normalmente), podemos visualizarlos de diferentes maneras.

Representación gráfica de sistemas lineales

Sistemas con 2 incógnitas: Si tienes dos variables (como x e y), cada ecuación lineal se puede dibujar como una recta en un plano cartesiano. La solución del sistema es el punto donde todas las rectas se cruzan. Si no se cruzan en un solo punto, el sistema no tiene una solución única.

La intersección de dos planos que no son paralelos coincidentes es una recta.

Sistemas con 3 incógnitas: Si tienes tres variables (como x, y y z), cada ecuación lineal representa un plano en un espacio tridimensional. La solución es el punto donde todos los planos se cruzan. Si se cruzan en una línea o en un plano completo, significa que hay infinitas soluciones.
Sistemas con más de 3 incógnitas: Para sistemas con cuatro o más variables, no podemos dibujarlos fácilmente, pero los conceptos matemáticos siguen siendo los mismos.

¿Qué tipos de sistemas lineales existen?

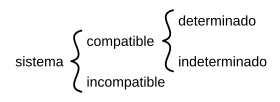
Los sistemas de ecuaciones se clasifican según cuántas soluciones tienen.

Sistema compatible: Es un sistema que sí tiene solución.
- Sistema compatible determinado: Tiene una única solución. Imagina que todas las líneas o planos se cruzan en un solo punto.
- Sistema compatible indeterminado: Tiene infinitas soluciones. Esto ocurre cuando las líneas o planos se superponen o se cruzan en una línea o superficie completa.
Sistema incompatible: Es un sistema que no tiene ninguna solución. Esto sucede cuando las líneas o planos son paralelos y nunca se cruzan.

Por ejemplo, si tienes dos ecuaciones que representan dos rectas paralelas, como:

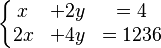
$\left \{ \begin{matrix} x & + 2y & = 4 \\ 2x & + 4y & = 1236 \end{matrix} \right .$

Estas dos rectas nunca se cruzan, por lo que no hay ningún par de valores (x, y) que satisfaga ambas ecuaciones al mismo tiempo. Es un sistema incompatible.

¿Cómo se resuelven los sistemas de ecuaciones lineales?

Existen varios métodos para encontrar las soluciones de un sistema de ecuaciones lineales. Aquí te explicamos algunos de los más comunes:

Método de Sustitución

Este método consiste en despejar una de las variables en una de las ecuaciones y luego reemplazar ese valor en las otras ecuaciones.

Por ejemplo, para resolver este sistema:

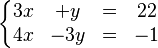
$\left \{ \begin{matrix} 3x & + y & = & 22 \\ 4x & - 3y & = & -1 \end{matrix} \right .$

1. Despejamos y de la primera ecuación: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = 22 - 3x . 2. Sustituimos este valor de y en la segunda ecuación: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4x - 3(22 - 3x) = -1 . 3. Resolvemos la nueva ecuación: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4x - 66 + 9x = -1 \Rightarrow 13x = 65 \Rightarrow x = 5 . 4. Ahora que sabemos que $x = 5$ , lo sustituimos en la ecuación de y: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = 22 - 3(5) \Rightarrow y = 22 - 15 \Rightarrow y = 7 . La solución es $x = 5$ e Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = 7 .

Método de Igualación

En este método, despejamos la misma variable en todas las ecuaciones y luego igualamos las expresiones resultantes.

Usando el mismo sistema anterior:

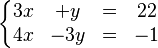
$\left \{ \begin{matrix} 3x & + y & = & 22 \\ 4x & - 3y & = & -1 \end{matrix} \right .$

1. Despejamos y de la primera ecuación: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = 22 - 3x . 2. Despejamos y de la segunda ecuación: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3y = 4x + 1 \Rightarrow y = \frac{4x + 1}{3} . 3. Igualamos las dos expresiones para y: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 22 - 3x = \frac{4x + 1}{3} . 4. Resolvemos para x: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3(22 - 3x) = 4x + 1 \Rightarrow 66 - 9x = 4x + 1 \Rightarrow 65 = 13x \Rightarrow x = 5 . 5. Sustituimos $x = 5$ en cualquiera de las ecuaciones originales para encontrar y, por ejemplo, en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = 22 - 3x , obtenemos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = 7 .

Método de Reducción

Este método busca eliminar una variable sumando o restando las ecuaciones. Para ello, a veces es necesario multiplicar una o ambas ecuaciones por un número para que los coeficientes de una variable sean iguales pero con signos opuestos.

Considera el sistema:

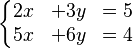
$\left \{ \begin{matrix} 2x & + 3y & = 5 \\ 5x & + 6y & = 4 \end{matrix} \right .$

1. Queremos eliminar y. Multiplicamos la primera ecuación por -2: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -2(2x + 3y = 5) \Rightarrow -4x - 6y = -10 . 2. Sumamos esta nueva ecuación a la segunda ecuación original: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rrcr} -4x & -6y & = & -10 \\ 5x & +6y & = & 4 \\ \hline x & & = & -6 \end{array} Así, obtenemos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = -6 . 3. Sustituimos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = -6 en la primera ecuación original: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2(-6) + 3y = 5 \Rightarrow -12 + 3y = 5 \Rightarrow 3y = 17 \Rightarrow y = \frac{17}{3} .

Método Gráfico

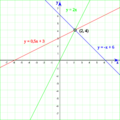
Este método es útil para sistemas con dos variables. Consiste en dibujar las rectas que representan cada ecuación.

Rectas que pasan por el punto: (2,4)

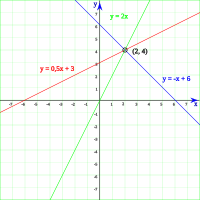
1. Despeja la variable y en ambas ecuaciones. 2. Crea una tabla de valores para cada ecuación (dando valores a x y calculando y). 3. Dibuja las rectas en un plano cartesiano. 4. Observa el punto de corte: * Si las rectas se cortan en un solo punto, esa es la única solución (sistema compatible determinado). * Si las rectas son la misma (coinciden), hay infinitas soluciones (sistema compatible indeterminado). * Si las rectas son paralelas y no se cortan, no hay solución (sistema incompatible).

Método de Gauss

Este método es más sistemático y se usa para sistemas con muchas ecuaciones. La idea es transformar el sistema en uno "escalonado", donde la última ecuación tiene solo una variable, la penúltima tiene dos, y así sucesivamente. Esto hace que sea muy fácil encontrar las soluciones de abajo hacia arriba.

Por ejemplo, para resolver un problema donde se reúnen 30 personas (hombres, mujeres y niños), y se dan pistas sobre sus cantidades:

Hombres (x), Mujeres (y), Niños (z)
Ecuación 1: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x + y + z = 30
Ecuación 2: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x + 3y = 2z + 20 \Rightarrow x + 3y - 2z = 20
Ecuación 3: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x + y = 2z \Rightarrow x + y - 2z = 0

El sistema ordenado es:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left \{ \begin{array}{rrrcr} x & +y & +z & = & 30 \\ x & +3y & -2z & = & 20 \\ x & +y & -2z & = & 0 \end{array} \right .

1. Restamos la primera ecuación a la segunda y a la tercera para eliminar x:

\left \{ \begin{array}{rrrcr} x & +y & +z & = & 30 \\ & 2y & -3z & = & -10 \\ & & -3z & = & -30 \end{array} \right .

2. De la tercera ecuación, obtenemos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -3z = -30 \Rightarrow z = 10 . 3. Sustituimos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): z = 10 en la segunda ecuación: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2y - 3(10) = -10 \Rightarrow 2y - 30 = -10 \Rightarrow 2y = 20 \Rightarrow y = 10 . 4. Sustituimos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = 10 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): z = 10 en la primera ecuación: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x + 10 + 10 = 30 \Rightarrow x = 10 . La solución es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = 10, y = 10, z = 10 .

Eliminación de Gauss-Jordan

Es una versión más avanzada del método de Gauss. En lugar de solo escalonar el sistema, lo transforma hasta que cada ecuación tiene una sola variable, lo que da directamente los valores de las incógnitas. Se trabaja con la matriz aumentada del sistema.

Regla de Cramer

Este método usa determinantes (un número especial calculado a partir de una matriz) para encontrar la solución. Es muy útil para sistemas pequeños (2x2 o 3x3) y cuando se busca una única solución.

Para un sistema de dos ecuaciones con dos incógnitas:

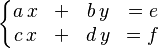
$\left \{ \begin{matrix} a \, x & + & b \, y & = e \\ c \, x & + & d \, y & = f \end{matrix} \right .$

Las soluciones se encuentran usando determinantes de la siguiente manera:

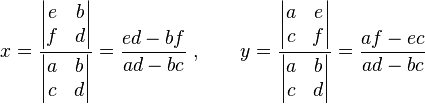
$x = \frac { \begin{vmatrix} e & b \\ f & d \end{vmatrix} } { \begin{vmatrix} a & b \\ c & d \end{vmatrix} } = { ed - bf \over ad - bc} \; , \qquad y = \frac { \begin{vmatrix} a & e \\ c & f \end{vmatrix} } { \begin{vmatrix} a & b \\ c & d \end{vmatrix} } = { af - ec \over ad - bc}$

Si el determinante de la matriz original (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ad - bc ) es cero, este método no funciona, lo que indica que el sistema no tiene una solución única o no tiene solución.

Galería de imágenes

La intersección de dos planos que no son paralelos coincidentes es una recta.
Clasificación de sistemas lineales.
Rectas que pasan por el punto: (2,4)

Véase también

En inglés: System of linear equations Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Sistema_de_ecuaciones_lineales&oldid=4980579»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Sistema de ecuaciones lineales para Niños. Enciclopedia Kiddle.