Matemáticas para niños
Las matemáticas son una ciencia muy importante que nos ayuda a entender el mundo. Surgieron del estudio de las formas (geometría) y de los números (aritmética). Hoy en día, muchos piensan que las matemáticas son la ciencia que investiga los patrones, es decir, las cosas que se repiten o tienen una estructura.
Las matemáticas nos permiten usar la lógica y el razonamiento para hacer cálculos y mediciones. También nos ayudan a estudiar las formas y el movimiento de los objetos. Desde sus inicios, las matemáticas han tenido un propósito práctico.
Contenido
¿Qué son las matemáticas?
Las matemáticas son una herramienta esencial en muchos campos. Se usan en las ciencias naturales (como la física o la química), en la medicina, en las ciencias sociales y hasta en la música y la literatura.
La utilidad de las matemáticas en la ciencia
Grandes pensadores han hablado sobre lo útiles que son las matemáticas. Por ejemplo, el físico Eugene Paul Wigner dijo que la gran utilidad de las matemáticas en las ciencias es algo misterioso. También, Galileo Galilei mencionó que el universo está escrito en lenguaje matemático, con triángulos, círculos y otras figuras geométricas. Esto significa que para entender el mundo, necesitamos las matemáticas.
Las matemáticas se dividen en dos grandes áreas:
- Matemáticas puras: Se enfocan en desarrollar nuevas ideas y teorías matemáticas sin pensar en una aplicación inmediata.
- Matemáticas aplicadas: Usan el conocimiento matemático para resolver problemas en otras áreas, como la ingeniería o la economía. A veces, estas aplicaciones inspiran nuevos descubrimientos en las matemáticas puras.
Un viaje por la historia de las matemáticas
Las matemáticas son una de las ciencias más antiguas.
Orígenes y primeros pasos
Las matemáticas florecieron primero en lugares como Mesopotamia, India y China. Más tarde, en la antigua Grecia, se empezó a usar la lógica para demostrar ideas matemáticas. Un ejemplo famoso son los Elementos de Euclides, un libro escrito por Euclides que organizó la geometría de forma lógica.
Durante la Edad Media, las matemáticas siguieron desarrollándose en las universidades y en el mundo árabe.
La era moderna y grandes descubrimientos
A principios de la era moderna, matemáticos como François Viète y René Descartes introdujeron nuevas formas de trabajar con números y formas.
Luego, Gottfried Leibniz e Isaac Newton desarrollaron el cálculo infinitesimal. Esta herramienta es fundamental para entender cómo cambian las cosas, como la velocidad de un objeto o el área bajo una curva. La mecánica clásica de Newton, que explica cómo se mueven los objetos, también impulsó muchos problemas matemáticos.
En los siglos siguientes, matemáticos como Niels Henrik Abel y Évariste Galois crearon el concepto de "grupo" para resolver ecuaciones complejas. Esto nos ayuda a entender las simetrías de los objetos.
La teoría de la probabilidad, que nos ayuda a entender las posibilidades de que algo ocurra, también tuvo un gran desarrollo gracias a pensadores como Blaise Pascal, Pierre de Fermat y Pierre-Simon Laplace.
A finales del siglo XIX, Georg Cantor desarrolló la teoría de conjuntos, que es muy importante en las matemáticas actuales.
Las matemáticas en el siglo XX y hoy
En el siglo XX, matemáticos como David Hilbert propusieron problemas importantes que impulsaron la investigación. Se buscó hacer las matemáticas más abstractas, es decir, reducir los objetos a sus propiedades más esenciales.
Hoy en día, las matemáticas siguen evolucionando y se usan en casi todos los campos del conocimiento.
¿Cómo se hacen las matemáticas?
Las matemáticas tienen su propio lenguaje, símbolos y una forma muy precisa de trabajar.
Notación y lenguaje matemático
La mayoría de los símbolos matemáticos que usamos hoy se inventaron en el siglo XVIII, gracias a matemáticos como Leonhard Euler. Antes, las matemáticas se escribían con palabras, lo que era muy lento.
La notación moderna hace que las matemáticas sean más fáciles para los expertos, pero puede ser un reto para los principiantes. Los símbolos matemáticos pueden contener mucha información en poco espacio.
El lenguaje matemático también es muy preciso. Palabras como "o" o "solo si" tienen un significado exacto en matemáticas, diferente al uso diario. También hay términos técnicos específicos, como "homeomorfismo". Esta precisión es lo que los matemáticos llaman "rigor".
El rigor en las demostraciones
El rigor es clave en las matemáticas. Significa que las demostraciones de los teoremas (afirmaciones que se prueban) deben seguir un razonamiento lógico y sistemático a partir de los axiomas (verdades básicas que se aceptan sin demostración). Esto ayuda a evitar errores y asegura que los resultados sean correctos.
El nivel de rigor ha cambiado con el tiempo. Los antiguos griegos eran muy detallistas, pero en la época de Isaac Newton los métodos eran menos rigurosos. Hoy, los matemáticos buscan demostraciones claras y elegantes.
¿Son las matemáticas una ciencia?
Hay mucho debate sobre si las matemáticas son una ciencia como la física o la biología.
La matemática como campo de conocimiento
Carl Friedrich Gauss, un famoso matemático, llamó a las matemáticas "la reina de las ciencias". Sin embargo, si definimos "ciencia" como el estudio del mundo físico a través de experimentos, entonces las matemáticas puras no encajan del todo, ya que no se basan en experimentos.
Algunos filósofos, como Karl Popper, dicen que las matemáticas no son una ciencia porque sus teorías no pueden ser "falsadas" experimentalmente (es decir, no se pueden probar que son incorrectas con un experimento). Sin embargo, otros piensan que las matemáticas sí son una ciencia porque exploran las consecuencias lógicas de las ideas y usan la intuición y la experimentación para formular nuevas ideas.
Premios y reconocimiento
Los premios matemáticos suelen ser diferentes de los premios científicos. El premio más prestigioso en matemáticas es la Medalla Fields, que se entrega cada cuatro años y se considera el equivalente al Premio Nobel para las matemáticas. Otros premios importantes son el Premio Wolf en matemática y el Premio Abel.
También existen listas de problemas matemáticos sin resolver, como los "Problemas de Hilbert" y los "Problemas del milenio". Resolver uno de estos problemas puede traer un gran reconocimiento y, en el caso de los Problemas del milenio, un premio de un millón de dólares.
Ramas de estudio de las matemáticas
Existen miles de ramas en las matemáticas, pero se pueden agrupar en algunas áreas principales:
Matemática pura
La matemática pura se enfoca en el estudio de los conceptos matemáticos por sí mismos, sin pensar en sus aplicaciones directas.
Cantidad
Esta área estudia los números y sus propiedades.
| 1, 2, 3, … | …, −2, −1, 0, 1, 2, … | −2, 2⁄3, 1,21 | −e, 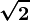 , 3, , 3, 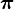 |
2, i, −2 + 3i,
2ei4π⁄3 |
| Números naturales | Enteros | Números racionales | Números reales | Números complejos |
Estructura
Esta rama estudia cómo se organizan las cosas y las relaciones entre ellas.
 |
 |
 |
 |
 |
|
| Combinatoria | Teoría de números | Teoría de grupos | Teoría de grafos | Teoría del orden | Álgebra |
Espacio
Esta área se ocupa de las formas, el tamaño, la posición y las propiedades del espacio.
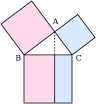 |
 |
 |
 |
 |
 |
| Geometría | Trigonometría | Geometría diferencial | Topología | Geometría fractal | Teoría de la medida |
Cambio
Esta rama estudia cómo las cosas cambian y se mueven.
 |
 |
 |
 |
 |
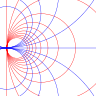 |
| Cálculo | Cálculo vectorial | Ecuaciones diferenciales | Sistemas dinámicos | Teoría del caos | Análisis complejo |
Matemática aplicada
La matemática aplicada usa las herramientas matemáticas para resolver problemas en otras áreas del conocimiento.
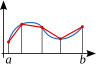
Estadística y toma de decisiones
La estadística es una parte de las matemáticas que estudia la variabilidad y los procesos aleatorios. Es fundamental para la investigación en muchos campos, como la informática, la ingeniería, la economía, la medicina y la psicología. Nos ayuda a recolectar, organizar y analizar datos para tomar decisiones inteligentes, incluso cuando hay incertidumbre.
Matemática computacional
Esta área combina las matemáticas con la computación para resolver problemas complejos.
 |
 |
 |
 |
 |
||
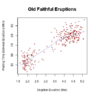
| Física matemática | Dinámica de fluidos | Análisis numérico | Optimización | Teoría de la probabilidad | Estadística | Criptografía |
 |
 |
 |
 |
 |
||
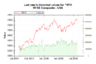
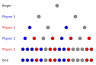
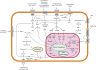
| Geometría computacional | Matemáticas financieras | Teoría de juegos | Biología matemática | Química matemática | Economía matemática | Teoría de control |
Galería de imágenes
-
Isaac Newton (1643-1727), codesarrollador del cálculo integral y diferencial.
-
Leonhard Euler. Uno de los matemáticos más productivos de la historia.
-
El símbolo de infinito en diferentes tipografías.
-
Carl Friedrich Gauss, apodado el «príncipe de los matemáticos».
-
El teorema de Pitágoras es uno de los enunciados más conocidos y antiguos de las matemáticas.
-
Un ábaco, instrumento para efectuar operaciones aritméticas sencillas.
Véase también
 En inglés: Mathematics Facts for Kids
En inglés: Mathematics Facts for Kids










