Numeración de Gödel para niños

La numeración de Gödel es una forma especial de asignar un número único a cada símbolo y a cada frase (o "fórmula") de un lenguaje de lógica o matemáticas. Imagina que es como un código secreto donde cada parte de una frase matemática tiene su propio número.

Esta idea fue creada por un matemático llamado Kurt Gödel. Él la usó para demostrar un teorema muy importante llamado el Teorema de Incompletitud de Gödel. Este teorema nos dice algo sorprendente sobre los sistemas matemáticos.

La numeración de Gödel también se usa para hablar de grupos de funciones que una computadora puede calcular. Es como si cada programa de computadora tuviera un número único.

¿Cómo funciona la Numeración de Gödel?

Para entender la numeración de Gödel, podemos pensar en ella como un proceso de varios pasos para convertir frases matemáticas en números.

Paso 1: Asignar números a los símbolos

Primero, cada símbolo que se usa en lógica o en aritmética recibe un número natural único. Es como darle un número de identificación a cada letra o signo.

Por ejemplo, algunos símbolos y sus números podrían ser:

Símbolos lógicos	Números
¬	1 (significa "no")
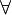	2 (significa "para todos")
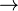	3 (significa "si, entonces")
(	6
)	7
0	9
=	10

Otros símbolos, como las letras que representan ideas (P, Q, R) o las variables (x, y, z), también reciben números especiales. La forma en que se asignan los números asegura que no haya confusiones entre los símbolos.

Paso 2: Convertir frases en números grandes

Una vez que cada símbolo tiene un número, podemos convertir una frase matemática completa en un solo número de Gödel. Para hacer esto, se usan los números primos (como 2, 3, 5, 7, 11, etc.).

La idea es multiplicar los números primos, elevando cada uno a la potencia del número de Gödel del símbolo correspondiente.

Por ejemplo, si tenemos la frase: 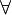x, P (x)

Y los códigos de los caracteres son:

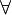• es 2
• x es 16
• P es 12
• ( es 6
• x es 16
• ) es 7

Entonces, la frase se convierte en: 2² × 3¹⁶ × 5¹² × 7⁶ × 11¹⁶ × 13⁷

Este número es muy, muy grande, pero es único para esa frase. Gracias a una regla matemática llamada el teorema fundamental de la aritmética, sabemos que cada número de Gödel solo puede descomponerse en sus factores primos de una única manera. Esto significa que siempre podemos "deshacer" el número de Gödel para obtener la frase original.

Paso 3: Numerar secuencias de frases

Finalmente, si tenemos una secuencia de frases, también podemos darles un número de Gödel. Se hace de forma similar, usando los números de Gödel de cada frase en la secuencia.

Por ejemplo, si tenemos:

• Frase 1 (con número de Gödel GN1)
• Frase 2 (con número de Gödel GN2)
• Frase 3 (con número de Gödel GN3)

La secuencia completa podría tener el número de Gödel: 2^GN1 × 3^GN2 × 5^GN3

Esto permite que las matemáticas hablen sobre sí mismas. Por ejemplo, podemos tener una frase que diga "la frase X se puede probar a partir de la frase Y". Esta relación también puede tener su propio número de Gödel.

¿Por qué es importante la Numeración de Gödel?

La numeración de Gödel fue clave para que Kurt Gödel demostrara su famoso teorema de incompletitud. Este teorema muestra que en cualquier sistema matemático lo suficientemente complejo, siempre habrá frases que son verdaderas pero que no se pueden demostrar dentro de ese mismo sistema.

Imagina una frase que, al ser convertida a su número de Gödel, dice algo como: "Esta frase no se puede demostrar".

• Si esta frase pudiera demostrarse, entonces sería falsa (porque dice que no se puede demostrar), lo que crea una contradicción.
• Si esta frase no pudiera demostrarse, entonces sería verdadera (porque dice que no se puede demostrar), lo que significa que el sistema matemático no es "completo" porque no puede demostrar todas las verdades.

Este descubrimiento cambió la forma en que los matemáticos entienden los límites de lo que se puede probar.

Galería de imágenes

• 

  Kurt Gödel (1906-1978), el matemático que creó esta idea.

Véase también

En inglés: Gödel numbering Facts for Kids