Fuerza para niños
Datos para niños Fuerza (F) |
||
|---|---|---|
 |
||
| Magnitud | Fuerza (F) | |
| Definición | Las fuerzas se pueden describir como aquello que empuja o tira de un objeto. Pueden deberse a fenómenos como la gravedad, el magnetismo o cualquier efecto que pueda provocar que una masa se acelere. | |
| Tipo | Magnitud vectorial | |
| Unidad SI | newton (N) Unidades base:kg·m/s2 | |
| Otras unidades | dina (MPa) kilopondio (kp) | |
En física, la fuerza (abreviatura F) es algo que puede cambiar el movimiento de un objeto o deformarlo. Imagina que empujas un carrito: estás aplicando una fuerza. Si lo frenas o cambias su dirección, también es una fuerza. Las fuerzas se pueden dibujar como flechas (vectores) porque tienen una dirección y una intensidad. Es importante no confundir la fuerza con el esfuerzo o la energía.
La unidad de medida de la fuerza en el Sistema Internacional de Unidades es el newton, que se escribe con el símbolo N. Este nombre es un homenaje a Isaac Newton, un científico muy importante que hizo grandes descubrimientos sobre la física y el movimiento. Un newton es la fuerza necesaria para que un objeto de 1 kilogramo aumente su velocidad en 1 metro por segundo cada segundo.
Otros conceptos relacionados con la fuerza son el empuje (que aumenta la velocidad), el arrastre (que la disminuye) y el par motor (que hace que un objeto gire más rápido o más lento). Cuando muchas fuerzas pequeñas actúan sobre un área de un objeto, hablamos de presión. Si estas fuerzas no están equilibradas, pueden hacer que el objeto se mueva. Las fuerzas también pueden causar que los materiales se deformen.
Contenido
La Fuerza en Física
La fuerza es una forma de describir cómo interactúan los objetos. Por ejemplo, la gravedad es la fuerza de atracción entre objetos que tienen masa. Tu peso es la fuerza con la que la Tierra te atrae. La fuerza elástica es la que hace un resorte cuando lo estiras o lo comprimes.
En física, la fuerza es una magnitud física que tiene dirección y puede deformar un cuerpo o cambiar su estado de movimiento o reposo. Esto significa que puede hacer que un objeto que estaba quieto se mueva, o que uno que ya se movía cambie su velocidad o dirección.
Cuando hablamos de la fuerza que aplicamos sobre un objeto, a menudo no pensamos en el otro objeto con el que está interactuando. Pero la fuerza siempre es una interacción entre dos o más objetos. Esto está relacionado con la tercera ley de Newton.
¿Cómo se desarrolló el concepto de fuerza?
Los filósofos de la Antigüedad ya estudiaban la fuerza al observar objetos quietos o en movimiento, y las máquinas simples. Sin embargo, pensadores como Aristóteles creían que para que un objeto se moviera a una velocidad constante, se necesitaba una fuerza continua. Esto era un error, en parte porque no entendían bien la fricción.
Galileo Galilei e Isaac Newton corrigieron estos errores. Newton, con sus conocimientos de matemáticas, formuló las leyes del movimiento que fueron muy importantes durante casi 300 años. Más tarde, en el siglo XX, Einstein desarrolló la teoría de la relatividad, que explicó cómo actúan las fuerzas en objetos que se mueven muy rápido, cerca de la velocidad de la luz, y también sobre la gravedad.
Hoy en día, la física de partículas ha creado un Modelo Estándar para describir las fuerzas entre partículas más pequeñas que los átomos. Este modelo dice que las fuerzas se transmiten mediante partículas llamadas bosones de gauge. Se conocen cuatro interacciones principales: la fuerza fuerte, la electromagnética, la fuerza débil y la fuerza gravitatoria.
Historia de la comprensión de la fuerza
El concepto de fuerza fue descrito por primera vez por Arquímedes, pero solo para objetos en reposo. Él y otros pensaban que el estado natural de los objetos en la Tierra era el reposo.
Galileo Galilei (1564-1642) fue el primero en dar una definición dinámica de fuerza. Él estableció la ley de la inercia, diciendo que un cuerpo sin ninguna fuerza actuando sobre él sigue moviéndose sin cambiar. Esta idea fue revolucionaria.
Se considera que Isaac Newton fue el primero en formular matemáticamente la definición moderna de fuerza. También propuso que la fuerza de la gravedad disminuye con el cuadrado de la distancia.
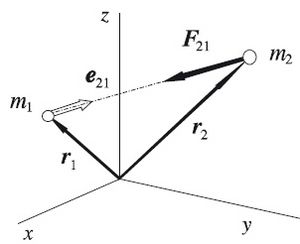
Charles Coulomb demostró que la interacción entre cargas eléctricas también sigue una ley similar (1784). En 1798, Henry Cavendish midió la fuerza de atracción gravitatoria entre dos masas pequeñas, lo que le permitió calcular la masa de la Tierra.
Con el desarrollo de la electrodinámica cuántica en el siglo XX, se entendió que la "fuerza" es una magnitud que surge de la conservación del momento lineal de las partículas. Por eso, las llamadas fuerzas fundamentales se conocen ahora como "interacciones fundamentales".
Ideas sobre la fuerza antes de Newton

Desde la Antigüedad, la fuerza se reconoció como parte de las máquinas simples. Arquímedes fue famoso por su estudio de las fuerzas de flotación en los fluidos.
Aristóteles creía que los objetos en la Tierra, hechos de tierra y agua, estaban en su "lugar natural" en el suelo y se quedarían allí si no se les molestaba. Él diferenciaba entre el "movimiento natural" (como una piedra cayendo) y el "movimiento no natural" o forzado, que necesitaba una fuerza continua. Esta teoría tenía problemas para explicar el movimiento de los proyectiles, como una flecha, ya que no parecía haber una fuerza continua empujándola. Aristóteles sugirió que el aire desplazado ayudaba a mover el proyectil.
Las ideas de Aristóteles fueron criticadas en la ciencia medieval. Las deficiencias de su física fueron corregidas por Galileo Galilei en el siglo XVII. Galileo hizo experimentos con piedras y balas de cañón rodando por una pendiente, demostrando que la gravedad acelera los cuerpos sin importar su masa. También argumentó que los objetos mantienen su velocidad a menos que una fuerza, como la fricción, actúe sobre ellos.
Las Leyes de Newton sobre el Movimiento
Primera Ley de Newton: La Inercia
La primera ley de Newton dice que un objeto seguirá moviéndose a una velocidad constante (o permanecerá en reposo) a menos que una fuerza externa actúe sobre él. Esta ley es una extensión de la idea de Galileo. Newton propuso que todos los objetos con masa tienen una inercia innata, que es su tendencia a resistir cambios en su estado de movimiento.
Por ejemplo, si vas en un coche que se mueve a velocidad constante y lanzas una pelota hacia arriba, la verás subir y bajar verticalmente. No necesitas aplicar una fuerza en la dirección del coche. Esto se debe a la inercia de la pelota, que la mantiene moviéndose hacia adelante con el coche. Desde tu punto de vista, el coche y todo dentro está en reposo.

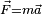 , en realidad escribió una forma diferente para su segunda ley del movimiento que no utilizaba cálculo diferencial.
, en realidad escribió una forma diferente para su segunda ley del movimiento que no utilizaba cálculo diferencial.Segunda Ley de Newton: Fuerza y Aceleración
La segunda ley de Newton se puede expresar con una ecuación:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \vec{F} = m\vec{a}
Esto significa que la fuerza (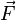 ) que actúa sobre un objeto es igual a su masa (m) multiplicada por su aceleración (
) que actúa sobre un objeto es igual a su masa (m) multiplicada por su aceleración (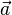 ). Si aplicas una fuerza mayor a un objeto, este acelerará más. Si el objeto tiene más masa, necesitarás una fuerza mayor para que acelere lo mismo.
). Si aplicas una fuerza mayor a un objeto, este acelerará más. Si el objeto tiene más masa, necesitarás una fuerza mayor para que acelere lo mismo.
Esta ley nos permite medir la fuerza. Por ejemplo, conociendo la masa de los planetas y cómo aceleran en sus órbitas, los científicos pueden calcular las fuerzas gravitatorias que actúan sobre ellos.
Tercera Ley de Newton: Acción y Reacción
Esta ley dice que por cada acción, hay una reacción igual y opuesta. Si un cuerpo ejerce una fuerza sobre otro, el segundo cuerpo ejerce una fuerza igual y en dirección contraria sobre el primero. A esta ley se le llama a veces "ley de acción-reacción".
Esto significa que todas las fuerzas son interacciones entre diferentes objetos. No existe una fuerza que actúe sobre un solo cuerpo. Por ejemplo, cuando empujas una pared, la pared te empuja a ti con la misma fuerza.
Si combinamos la segunda y tercera ley de Newton, podemos entender que el momento lineal de un sistema se mantiene constante si no hay fuerzas externas actuando sobre él.
La Fuerza en la Mecánica Clásica
En la mecánica clásica, la fuerza se puede definir como el cambio del momento lineal de un objeto a lo largo del tiempo. Si la masa del objeto no cambia, la fuerza es igual a la masa multiplicada por la aceleración ( ). Esta es la forma más conocida de la segunda ley de Newton.
). Esta es la forma más conocida de la segunda ley de Newton.
Tipos de Fuerzas: Contacto y a Distancia
Aunque todas las fuerzas naturales son interacciones a distancia, para entenderlas mejor, las dividimos en dos tipos:
- Fuerzas de contacto: Son las que ocurren cuando dos objetos se tocan directamente, como cuando empujas una caja.
- Fuerzas a distancia: Son las que actúan sin que los objetos se toquen, como la fuerza gravitatoria (la Tierra te atrae sin tocarte) o la fuerza entre cargas eléctricas.
Fuerzas Internas y de Contacto en Sólidos
En los objetos sólidos, los átomos tienen sus electrones organizados en capas, lo que hace que la materia sea "impenetrable" a nivel macroscópico. Esto significa que cuando dos cuerpos se tocan, sus electrones externos se repelen, creando fuerzas que impiden que se superpongan.
Las fuerzas internas dentro de un material sólido son más complejas y se describen con un tensor de tensiones. En los líquidos, las fuerzas internas dependen de la presión y, si el líquido se mueve, también de la viscosidad.
Fricción
Fricción La fricción es una fuerza que aparece cuando dos superficies se deslizan una sobre otra. En la mecánica de Newton, la fricción entre sólidos se modela como una fuerza que actúa de forma paralela a las superficies en contacto y es proporcional a la fuerza que las presiona entre sí (fuerza normal).
La fricción entre un sólido y un líquido, o dentro de un líquido o gas, depende de cómo fluye el fluido (si es laminar o turbulento).
Fuerza Gravitatoria
La fuerza gravitatoria es la fuerza de atracción entre dos objetos con masa. Cuanto más masivos son los objetos y más cerca están, mayor es la fuerza. La ley de la gravitación universal de Newton describe esta fuerza.
Cuando uno de los objetos es mucho más grande que el otro (como un planeta y una persona), la fórmula se simplifica y se relaciona con la gravedad (g).
Fuerza Eléctrica
La fuerza eléctrica también actúa a distancia. A diferencia de la gravedad, que siempre atrae, la fuerza eléctrica puede ser de atracción o de repulsión. Las cargas eléctricas opuestas se atraen, y las cargas iguales se repelen.
Unidades de Fuerza
La unidad de fuerza en el Sistema Internacional de Unidades (SI) es el newton (N). Otras unidades incluyen:
- Sistema Técnico de Unidades: kilogramo-fuerza (kgf) o kilopondio (kp)
- Sistema Cegesimal de Unidades: dina (dyn)
- Sistema anglosajón de unidades: Poundal, Libra fuerza (lbf)
- Equivalencias
- 1 newton = 100 000 dinas
- 1 kilogramo-fuerza = 9,80665 newtons
- 1 libra fuerza ≡ 4,448222 newtons
Interacciones Fundamentales

En la física moderna, especialmente en la teoría cuántica de campos, el término "fuerza fundamental" se refiere a las formas básicas en que la materia y los campos interactúan en el Universo. Se consideran cuatro interacciones fundamentales:
- La fuerza gravitatoria: Es la atracción entre objetos con masa. Es la más débil de las cuatro, pero tiene un alcance infinito y siempre atrae.
- La fuerza electromagnética: Afecta a los objetos con carga eléctrica. Es la responsable de las transformaciones químicas y físicas de átomos y moléculas. Es mucho más fuerte que la gravedad, puede atraer o repeler, y también tiene un alcance infinito.
- La fuerza nuclear fuerte: Es la que mantiene unidos los componentes del núcleo de los átomos (protones y neutrones). Es la más intensa de todas, pero su alcance es muy corto, solo dentro del núcleo.
- La fuerza nuclear débil: Es la responsable de algunos tipos de desintegración radiactiva. Su alcance es aún más corto que el de la fuerza fuerte.
Es importante saber que los científicos sospechan que estas "fuerzas fundamentales" podrían ser diferentes manifestaciones de una única fuerza más grande, que aún no hemos descubierto por completo.
Galería de imágenes
Véase también
 En inglés: Force Facts for Kids
En inglés: Force Facts for Kids