Jacob Bernoulli para niños
Datos para niños Jacob Bernoulli |
||
|---|---|---|
 |
||
| Información personal | ||
| Nombre en alemán | Jakob Bernoulli | |
| Nacimiento | 27 de diciembre de 1654 |
|
| Fallecimiento | 16 de agosto de 1705 |
|
| Sepultura | Catedral de Basilea | |
| Residencia | Suiza | |
| Nacionalidad | Suiza | |
| Familia | ||
| Familia | Familia Bernoulli | |
| Padres | Nicolau Bernoulli Margaretha Bernoulli |
|
| Cónyuge | Judith Stupanus | |
| Educación | ||
| Educación | doctor en Filosofía | |
| Educado en | Universidad de Basilea | |
| Supervisor doctoral | Nicolas Malebranche y Peter Werenfels | |
| Alumno de | Gottfried Leibniz | |
| Información profesional | ||
| Área | Teoría de probabilidad Cálculo diferencial Teoría de números Geometría |
|
| Conocido por | Ecuación diferencial de Bernoulli Polinomios de Bernoulli Ensayo de Bernoulli Ley de los grandes números Lemniscata |
|
| Empleador | Universidad de Basilea | |
| Estudiantes doctorales | Johann Bernoulli Jacob Hermann Nicolaus I Bernoulli |
|
| Obras notables |
|
|
| Miembro de |
Academia Prusiana de las Ciencias Academia de Ciencias de Francia |
|
| Notas | ||
| Hermano de Johann Bernoulli | ||
Jacob Bernoulli (nacido en Basilea, Suiza, el 27 de diciembre de 1654, y fallecido allí el 16 de agosto de 1705), también conocido como Jakob, Jacques o James Bernoulli, fue un importante matemático y científico suizo. Era el hermano mayor de Johann Bernoulli, y ambos formaron parte de la famosa Familia Bernoulli, conocida por sus muchos talentos en la ciencia.
Jacob es famoso por sus grandes aportaciones al cálculo, una rama de las matemáticas que estudia el cambio y el movimiento. Junto con su hermano Johann, fue uno de los pioneros en el cálculo de variaciones, que ayuda a encontrar las mejores formas o caminos para ciertos problemas. También descubrió una constante matemática muy importante, conocida como e.
Apoyó las ideas de Gottfried Wilhelm Leibniz sobre el cálculo y fue uno de los primeros en usar y mejorar este nuevo método matemático. Sin embargo, su trabajo más influyente fue en el campo de la probabilidad, donde desarrolló la primera versión de la ley de los grandes números en su libro Ars Conjectandi.
Contenido
¿Quién fue Jacob Bernoulli?
Jacob Bernoulli nació en una familia de comerciantes en Basilea. Sus padres fueron Nicolas Bernoulli y Margaretha Schönauer. Su padre era un exitoso importador de especias. Aunque la familia tenía una tradición en el comercio, Jacob mostró una gran inteligencia desde pequeño.
Su padre quería que estudiara filosofía y teología en la Universidad de Basilea para convertirse en teólogo. Sin embargo, Jacob se sintió atraído por las matemáticas, la física y la astronomía. Antes de terminar sus estudios, ya sabía que su verdadera pasión era la ciencia.
Su padre no estuvo de acuerdo al principio, así que Jacob se mudó a Ginebra por un año para trabajar como profesor de matemáticas. Con el tiempo, su padre aceptó su vocación e incluso le ayudó a financiar un viaje por Europa. Durante este viaje, Jacob pudo conocer a los científicos más importantes de su época.
Su carrera y descubrimientos
En 1676, durante un viaje a Inglaterra, Jacob Bernoulli conoció a científicos como Robert Boyle y Robert Hooke. Estas experiencias lo inspiraron a dedicar su vida a la ciencia y las matemáticas.
En 1682, fue nombrado Lector en la Universidad de Basilea, y en 1687, se convirtió en Profesor de Matemáticas en la misma universidad. Desde entonces y hasta su fallecimiento, enseñó y continuó sus investigaciones.
Jacob fue uno de los primeros en desarrollar el cálculo más allá de lo que habían logrado Isaac Newton y Gottfried Wilhelm Leibniz. Aplicó estas nuevas ideas a problemas complejos e importantes. Sus aportaciones a la geometría analítica, la teoría de probabilidad y el cálculo de variaciones fueron muy significativas.
En 1690, fue la primera persona en crear una técnica para resolver un tipo de ecuación diferencial llamada "ecuaciones diferenciales separables".
Aprendió sobre el cálculo gracias a su comunicación con Gottfried Leibniz. Trabajó con su hermano Johann en varias aplicaciones, publicando artículos sobre curvas trascendentales (1696) e isoperimetría (1700, 1701).
Su obra más importante fue Ars Conjectandi (El Arte de la Conjetura), un libro fundamental en la teoría de la probabilidad. Fue publicado por su sobrino Nicholas en 1713, ocho años después de su muerte. Términos como ensayo de Bernoulli y números de Bernoulli provienen de su trabajo.
Aportaciones al Cálculo
Jacob y su hermano Johann fueron grandes seguidores de las ideas de Gottfried Wilhelm Leibniz sobre el cálculo. Ellos creían en los infinitesimales (cantidades muy, muy pequeñas) como elementos matemáticos reales. Los usaron para obtener resultados importantes tanto en el cálculo como en su aplicación a problemas de física.
Fueron de los primeros en Europa en entender las nuevas técnicas de Leibniz y aplicarlas para resolver problemas nuevos y antiguos. Por ejemplo, Jacob encontró la ecuación diferencial de la curva isócrona. Esta curva es importante porque ayuda a entender cómo funciona el péndulo matemático en los relojes.
También trabajaron en el problema de la curva catenaria, que es la forma que toma una cadena o cable cuando cuelga libremente entre dos puntos. Galileo Galilei había pensado que era una parábola, pero Jacob propuso el problema y su hermano Johann lo resolvió en 1691. Este fue el comienzo de algunas rivalidades entre los hermanos.
La Espiral Logarítmica
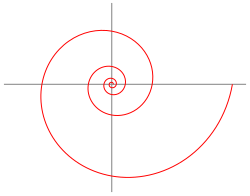
Jacob Bernoulli estaba fascinado por la espiral logarítmica. Esta espiral es especial porque, a medida que crece, sus brazos se separan de una manera que mantiene la misma forma. Él la llamó Spira mirabilis, que significa "la espiral maravillosa".
Bernoulli pidió que se grabara una espiral logarítmica en su tumba, junto con la frase en latín "Eadem mutata resurgo". Esta frase significa "Mutante y permanente, vuelvo a resurgir siendo el mismo". Quería que la espiral simbolizara la fortaleza y la constancia, o incluso la idea de que el cuerpo humano, después de muchos cambios, volverá a su forma perfecta.
Sin embargo, los tallistas de la tumba grabaron por error una espiral de Arquímedes. La diferencia es que en la espiral de Arquímedes, las distancias entre los brazos son siempre iguales, mientras que en la espiral logarítmica, estas distancias aumentan de forma proporcional.
Descubrimiento de la Constante e
En 1683, Jacob Bernoulli descubrió la constante matemática e mientras estudiaba un problema sobre el interés compuesto. Quería saber cuánto dinero se obtendría si el interés se calculaba y se añadía al capital de forma continua, en lugar de solo una vez al año.
Imagina que tienes $1.00 y ganas un 100% de interés anual.
- Si el interés se calcula una vez al año, al final tendrás $2.00.
- Si se calcula dos veces al año, tendrás $1.00 multiplicado por 1.5 dos veces, lo que da $2.25.
- Si se calcula cada tres meses (cuatro veces al año), tendrás $1.00 multiplicado por 1.25 cuatro veces, lo que da $2.4414...
- Si se calcula cada mes, el resultado es $2.613035...
Bernoulli se dio cuenta de que a medida que el interés se calculaba en intervalos cada vez más pequeños (semanalmente, diariamente, o incluso de forma continua), el valor se acercaba a un límite. Este límite es el número que más tarde Leonhard Euler llamó e. Su valor aproximado es 2.7182818....
Aportaciones a la Probabilidad
La obra más original de Jacob Bernoulli se encuentra en la teoría de la probabilidad. Se le considera el fundador de la teoría matemática de la probabilidad gracias a su libro Ars Conjectandi, que se publicó después de su muerte en 1713. Este libro fue el resultado de veinte años de investigación.
Antes de Bernoulli, los cálculos de probabilidad (hechos por científicos como Blaise Pascal y Pierre de Fermat) se limitaban a juegos de azar. Jacob Bernoulli quería calcular probabilidades en situaciones donde no se pueden enumerar todas las posibilidades.
Por ejemplo, es fácil calcular la probabilidad de que salga un número específico al lanzar un dado (1/6). Pero para calcular la probabilidad de que una persona de ochenta años viva diez años más, no se puede usar el mismo método. Para esto, Bernoulli introdujo la ley de los grandes números, que aparece en la cuarta parte de su libro. Esta ley dice que si se repite un experimento muchas veces, la frecuencia de un evento se acercará a su probabilidad teórica.
Las primeras tres partes de su libro se basan en trabajos anteriores, pero la cuarta parte, titulada "Sobre el uso y aplicaciones de la Doctrina en la Política, la Ética y la Economía", representa un gran avance en el concepto de probabilidad.
Reconocimientos
- El cráter lunar Bernoulli lleva este nombre en honor a Jacob y a su hermano Johann Bernoulli.
- El asteroide (2034) Bernoulli también conmemora su nombre y los de Johann Bernoulli y Daniel Bernoulli.
Véase también
 En inglés: Jacob Bernoulli Facts for Kids
En inglés: Jacob Bernoulli Facts for Kids
- Familia Bernoulli
- Johann Bernoulli
- Teorema de Bernoulli
- Espiral logarítmica
- Ensayo de Bernoulli

