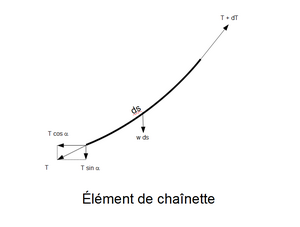
Catenaria para niños
Una catenaria es una curva especial que se forma cuando una cadena, cuerda o cable cuelga libremente de sus dos extremos. Imagina una cadena que no es rígida y que solo está sostenida por sus puntas, como un collar colgando. La forma que toma esa cadena es una catenaria. La palabra viene del latín catēnarĭus, que significa "propio de la cadena".
Contenido
¿Qué es una Catenaria?
La forma de una cadena colgante
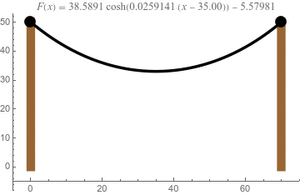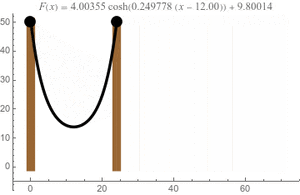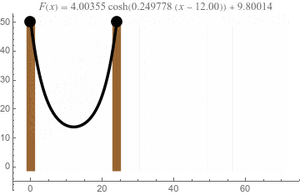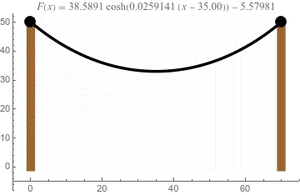
La catenaria es la forma natural que adopta un cable o una cadena cuando cuelga libremente entre dos puntos, bajo el efecto de su propio peso. Es una curva muy común que podemos ver en muchos lugares a nuestro alrededor.
¿Por qué es importante la catenaria?
Esta curva es importante en la ingeniería y la arquitectura porque ayuda a entender cómo se distribuyen las fuerzas en estructuras colgantes. Conocer la forma de la catenaria permite diseñar puentes, cables eléctricos y arcos de manera más segura y eficiente.
Historia de la Catenaria
El misterio de la cadena colgante
En el siglo XVII, muchos científicos y matemáticos se preguntaban qué forma exacta tomaba una cadena colgante. Al principio, algunos pensaron que era una parábola, una curva que se parece mucho a la catenaria, especialmente en tramos cortos.
El descubrimiento de Christiaan Huygens
Fue Christiaan Huygens, un científico muy joven en ese momento, quien demostró que la curva no era una parábola. Aunque se parecían, no eran exactamente iguales. Huygens fue el primero en usar la palabra "catenaria" para describir esta curva en una carta en 1690.
La ecuación de la catenaria
La ecuación matemática que describe la catenaria fue descubierta en 1691 por varios matemáticos importantes: Gottfried Leibniz, el propio Christiaan Huygens y Johann Bernoulli. Ellos resolvieron el desafío que había propuesto Jakob Bernoulli, otro matemático famoso.
La Matemática de la Catenaria
¿Cómo se describe la catenaria con números?
La catenaria tiene una ecuación matemática específica que la describe. Si colocamos el punto más bajo de la curva en el eje Y de un gráfico, su ecuación es:
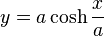
Aquí, la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cosh es el "coseno hiperbólico", que es una función matemática especial. El valor de 'a' depende de qué tan "colgada" esté la cadena.
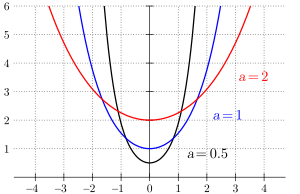
¿Es una parábola?
Aunque la catenaria se parece mucho a una parábola, especialmente cerca de su punto más bajo, no son la misma curva. La catenaria es un poco más "ancha" en los extremos que una parábola.
Propiedades de la Catenaria
Características de esta curva especial
Una catenaria tiene varias características interesantes:
- El punto más bajo de la curva se llama vértice.
- Es una curva simétrica, lo que significa que si la doblas por la mitad, ambos lados coinciden.
- La longitud de un trozo de la curva se puede calcular con una fórmula específica.
Cadenas reales vs. Catenarias ideales
Las catenarias que vemos en la vida real, como los cables de la luz o las cadenas de un columpio, son muy parecidas a la catenaria ideal. Sin embargo, las cadenas reales no son "infinitamente flexibles" ni "inextensibles" (que no se estiran), como se asume en la teoría. Aun así, la forma es casi idéntica.
Aplicaciones de la Catenaria
¿Dónde podemos ver catenarias?
La forma de la catenaria es muy útil en la construcción y la ingeniería:
- Puentes colgantes: Los cables principales de muchos puentes colgantes forman una catenaria.
- Cables eléctricos: Los cables de alta tensión que cuelgan entre postes también adoptan esta forma.
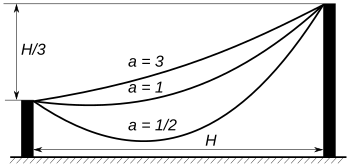
- Arquitectura: Algunos arquitectos, como el famoso Antonio Gaudí, usaron la forma de la catenaria invertida para diseñar arcos. Un arco con forma de catenaria invertida es muy fuerte porque distribuye el peso de manera eficiente, evitando que se rompa. Gaudí incluso usaba maquetas con cadenas colgantes para diseñar sus edificios, como la Sagrada Familia en Barcelona.

Véase también
 En inglés: Catenary Facts for Kids
En inglés: Catenary Facts for Kids
- Funciones hiperbólicas
- Coseno hiperbólico
- Catenoide
- Polígono funicular


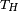 =
= 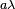 , donde
, donde  es la masa por unidad de longitud.
es la masa por unidad de longitud.