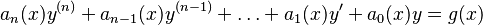Ecuación diferencial para niños
Una ecuación diferencial es una ecuación matemática que conecta una función con sus derivadas. Piensa en una función como una regla que te dice cómo se comporta algo, y una derivada como la forma en que ese algo cambia. Por ejemplo, si tienes una función que describe la posición de un coche, su derivada te dirá qué tan rápido se mueve (su velocidad).
En el mundo real, las funciones suelen representar cosas físicas, como la temperatura de un objeto o la cantidad de una población. Las derivadas nos muestran cómo cambian esas cosas. Una ecuación diferencial, entonces, nos ayuda a entender la relación entre una cantidad y cómo cambia.
Como estas relaciones son muy comunes, las ecuaciones diferenciales son muy importantes en muchas áreas. Se usan en ingeniería para diseñar puentes, en física para entender el movimiento de los planetas, en química para estudiar reacciones, en economía para predecir mercados y en biología para modelar el crecimiento de poblaciones.
A veces, no podemos encontrar una fórmula exacta para resolver una ecuación diferencial. En esos casos, podemos usar computadoras para encontrar soluciones aproximadas. Esto es muy útil, ya que nos permite predecir cómo se comportarán las cosas incluso si no tenemos una respuesta perfecta.
Contenido
Historia de las Ecuaciones Diferenciales
Las ecuaciones diferenciales aparecieron por primera vez en los trabajos de cálculo de Newton y Leibniz en el siglo XVII. Newton, en 1671, en su libro Método de las fluxiones y series infinitas, ya mencionaba diferentes tipos de ecuaciones diferenciales. Él las resolvía usando series infinitas.
En 1695, Jakob Bernoulli propuso una ecuación diferencial que lleva su nombre, la ecuación diferencial de Bernoulli. Poco después, Leibniz encontró formas de resolverla.
Históricamente, el estudio de cómo vibra una cuerda, como la de un instrumento musical, fue muy importante. Científicos como Jean le Rond d'Alembert, Leonhard Euler, Daniel Bernoulli y Joseph-Louis Lagrange investigaron este problema.
En 1746, d'Alembert descubrió la ecuación de onda para una dimensión, y diez años después, Euler encontró la ecuación de onda para tres dimensiones. Estas ecuaciones describen cómo se propagan las ondas, como el sonido o la luz.
Las ecuaciones de Euler-Lagrange fueron desarrolladas en la década de 1750 por Euler y Lagrange. Esto ocurrió mientras estudiaban el problema de la tautócrona, que busca la curva por la que una partícula tarda el mismo tiempo en caer a un punto fijo, sin importar desde dónde empiece.
En 1822, Joseph Fourier publicó su trabajo sobre la transferencia de calor. En él, explicó la ecuación del calor, que describe cómo se difunde el calor en un material. Esta ecuación es fundamental en la física matemática.
Más tarde, en los años 1940 y 1950, Kiyoshi Itō y Ruslán Stratónovich introdujeron las ecuaciones diferenciales estocásticas, que combinan las ecuaciones diferenciales con la teoría de la probabilidad.
Tipos de Ecuaciones Diferenciales
Las ecuaciones diferenciales se pueden clasificar de varias maneras, lo que ayuda a saber cómo resolverlas. Algunas de las clasificaciones más comunes son:
Ecuaciones Diferenciales Ordinarias (EDO)
Una Ecuación Diferencial Ordinaria (EDO) es una ecuación que tiene una función que depende de una sola variable y sus derivadas. La palabra "ordinaria" se usa para distinguirlas de las ecuaciones en derivadas parciales, que tienen más de una variable.
Las EDO lineales son más fáciles de resolver y a menudo tienen soluciones exactas. Las EDO no lineales son más complejas y sus soluciones exactas son raras. Sin embargo, se pueden usar métodos numéricos y computadoras para encontrar soluciones aproximadas, que son muy útiles en la práctica.
Ecuaciones en Derivadas Parciales (EDP)
Una Ecuación en Derivadas Parciales (EDP) es una ecuación diferencial que contiene una función que depende de varias variables y sus derivadas parciales. Estas ecuaciones se usan para describir problemas que involucran funciones de múltiples variables, como la temperatura en una habitación (que depende de la posición y el tiempo).
Las EDP se usan para describir muchos fenómenos, como el sonido, el calor, la electroestática, el movimiento de fluidos y la mecánica cuántica. Son muy útiles para crear simulaciones de sistemas complejos.
Ecuaciones Diferenciales Lineales
Una ecuación diferencial es lineal si sus soluciones se pueden combinar de forma sencilla (sumar o multiplicar por números) para formar nuevas soluciones. En una ecuación lineal, la función desconocida y sus derivadas no están elevadas a ninguna potencia mayor que uno, y no hay productos entre ellas.
Las ecuaciones lineales son importantes porque su teoría está bien desarrollada y a menudo se pueden resolver de forma más directa.
Un ejemplo de una ecuación diferencial lineal es:
Esto significa que:
- Ni la función ni sus derivadas están elevadas a potencias diferentes de uno o cero.
- Los números que las multiplican (coeficientes) solo dependen de la variable independiente.
- Si tienes varias soluciones, al sumarlas o multiplicarlas por números, el resultado también es una solución.
Ejemplos:
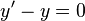es una ecuación lineal de primer orden.
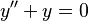es una ecuación lineal de segundo orden.
Ecuaciones Diferenciales No Lineales
Las ecuaciones diferenciales no lineales son mucho más difíciles de resolver de forma exacta. A menudo, exhiben un comportamiento muy complejo, que a veces se relaciona con la teoría del caos.
Estas ecuaciones aparecen cuando se hacen aproximaciones a ecuaciones lineales. Por ejemplo, el movimiento de un péndulo se describe con una ecuación no lineal, pero para pequeños movimientos, se puede aproximar con una ecuación lineal (la del oscilador armónico).
Orden de la Ecuación
El orden de una ecuación diferencial se determina por la derivada de mayor orden que aparece en ella.
- Una ecuación con solo derivadas simples (como
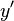) es de primer orden. - Una ecuación con derivadas segundas (como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y'' ) es de segundo orden.
- Y así sucesivamente.
Ejemplos:
- Primer orden:
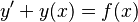
- Segundo orden:
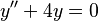
- Tercer orden:
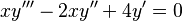
Solución de una Ecuación Diferencial
Encontrar la solución de una ecuación diferencial es diferente a resolver una ecuación algebraica. A veces, lo más importante es saber si una solución existe y si es única.
Tipos de Soluciones
Una solución de una ecuación diferencial es una función que, al ser sustituida en la ecuación junto con sus derivadas, hace que la ecuación sea verdadera. Hay tres tipos principales de soluciones:
Solución General
La solución general es una solución que incluye una o más constantes. Representa una familia de curvas. Por ejemplo, si la solución tiene una constante, significa que hay infinitas curvas que satisfacen la ecuación, y cada una se obtiene dándole un valor diferente a esa constante.
Solución Particular
Una solución particular es un caso específico de la solución general. Se obtiene cuando se le da un valor concreto a la constante (o constantes) de la solución general. Esto suele ocurrir cuando se nos da una condición inicial, como un punto específico por el que debe pasar la curva de la solución.
Solución Singular
Una solución singular es una función que también satisface la ecuación diferencial, pero que no se puede obtener a partir de la solución general dándole un valor a las constantes. Es como una solución "especial" que existe fuera de la familia de curvas de la solución general.
Aplicaciones de las Ecuaciones Diferenciales
Las ecuaciones diferenciales son una herramienta muy poderosa en muchas áreas de las matemáticas puras y aplicadas, la física y la ingeniería. Son esenciales para crear modelos matemáticos de casi cualquier proceso físico, técnico o biológico. Por ejemplo, se usan para describir el movimiento de los planetas, el diseño de un puente o cómo interactúan las neuronas.
Muchas leyes de la física y la química se escriben usando ecuaciones diferenciales. En biología y economía, se usan para modelar el comportamiento de sistemas complejos. A veces, diferentes problemas en campos distintos resultan en la misma ecuación diferencial. Esto demuestra que, detrás de la matemática, puede haber un principio unificado que explica fenómenos aparentemente diferentes. Por ejemplo, la propagación de la luz, el sonido y las ondas en el agua pueden describirse con la misma ecuación en derivadas parciales de segundo orden, la ecuación de onda.
Física
- Leyes de Newton en mecánica clásica: Permiten describir el movimiento de una partícula si se conoce la fuerza que actúa sobre ella.
- Ecuación de onda: Describe cómo se propagan las ondas (sonido, luz, ondas en el agua).
- Ecuación de calor: Explica cómo se difunde el calor.
- Ecuaciones de Maxwell: Son fundamentales para entender la electrodinámica, la óptica y los circuitos eléctricos. Describen cómo los campos eléctricos y magnéticos se generan e interactúan.
- Relatividad general: Las ecuaciones de campo de Einstein describen cómo la gravitación es el resultado de que el espacio-tiempo se curva debido a la presencia de materia y energía.
- Mecánica cuántica: La Ecuación de Schrödinger describe cómo evolucionan los sistemas cuánticos (como átomos y moléculas) a lo largo del tiempo.
Biología
- Ecuación de Verhulst: Se usa para modelar el crecimiento de poblaciones biológicas.
- Modelo de von Bertalanffy: Describe el crecimiento individual de organismos.
- Modelo de Hodgkin y Huxley: Explica los potenciales de acción en las neuronas.
Ecuaciones Predador-Presa
Las ecuaciones de Lotka-Volterra (también llamadas ecuaciones predador-presa) son un par de ecuaciones diferenciales no lineales que se usan para describir cómo interactúan dos especies en un ecosistema: una que es el predador y otra que es la presa.
Crecimiento de Poblaciones
En el siglo XVIII, los científicos querían predecir cómo cambiaría el tamaño de las poblaciones. El economista T. Malthus propuso un modelo simple: Los nacimientos y las muertes en un corto tiempo son proporcionales al tamaño de la población y al tiempo. Esto llevó a la ecuación: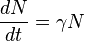 
Donde 
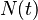es el tamaño de la población en el tiempo 
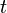, y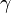 
es una constante. La solución de esta ecuación es 
.
- Si
, la población disminuye. - Si
, la población se mantiene constante. - Si
, la población crece muy rápido (exponencialmente).
Más tarde, Verhulst propuso una modificación al modelo de Malthus, reconociendo que las poblaciones no pueden crecer sin límite, sino que tienden a estabilizarse en un tamaño máximo. Su modelo es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {dN \over dt} = \gamma N\left (1 - {N \over N_\infty} \right ) Donde Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): N_\infty es el límite máximo de la población. La solución de este modelo es:
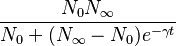Este modelo es más realista para describir el crecimiento de poblaciones en el mundo real.
Software para Ecuaciones Diferenciales
Existen programas de computadora que pueden ayudar a resolver ecuaciones diferenciales o a encontrar sus soluciones aproximadas:
- ExpressionsinBar
- Maple
- SageMath
- Xcas
Véase también
En inglés: Differential equation Facts for Kids
- Historia de las ecuaciones diferenciales
- Sistema de ecuaciones diferenciales
- Función diferenciable
- Ecuación integral
Galería de imágenes
-
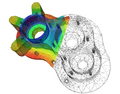
Visualización de transferencia de calor en una cámara de una bomba, creada resolviendo la ecuación de calor. El calor se genera internamente en la cámara y se enfría en los bordes, dando un estado estacionario de distribución de temperatura.
-
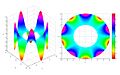
Ecuación de Laplace sobre una corona (r=2 y R=4) con condiciones de contorno de Dirichlet: u(r=2)=0 y u(r=4)=4sen(5*θ).
-
La masa colgada del resorte forma un oscilador armónico, una ecuación diferencial permite expresar las relaciones que debe obedecer el movimiento de la masa.
