Matemáticas y arte para niños
Las matemáticas y el arte están muy conectadas. A menudo, las matemáticas se describen como un arte por su belleza y elegancia. Podemos ver su presencia en la música, la danza, la pintura, la arquitectura, la escultura y las artes textiles.
Este artículo se enfoca en cómo las matemáticas han influido en las artes visuales, es decir, en lo que podemos ver.
Las matemáticas y el arte tienen una larga historia juntos. Desde hace mucho tiempo, ha habido artistas que también eran matemáticos. Por ejemplo, en el siglo IV antes de Cristo, el escultor griego Policleto escribió un libro llamado "Canon". En él, explicaba cómo usar proporciones basadas en la relación 1:√2 para crear la figura ideal del cuerpo masculino.
Durante el Renacimiento en Italia, Luca Pacioli escribió un libro muy importante llamado De divina proportione (1509). Este libro, ilustrado por Leonardo da Vinci, hablaba sobre cómo usar la proporción áurea en el arte. Otro pintor italiano, Piero della Francesca, desarrolló las ideas de Euclides sobre la perspectiva en sus escritos y pinturas. El artista Alberto Durero también incluyó muchas referencias matemáticas en sus obras, como en su grabado Melancolía I.
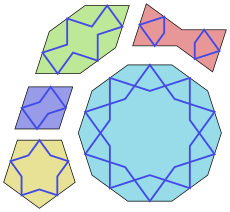
En tiempos más recientes, el artista M. C. Escher usó mucho los teselados (patrones que cubren una superficie sin dejar huecos) y la geometría hiperbólica con la ayuda del matemático Harold Scott MacDonald Coxeter. El movimiento artístico De Stijl, liderado por Theo van Doesburg y Piet Mondrian, usó formas geométricas de manera muy clara.
Las matemáticas también han inspirado las artes textiles, como el quilting (acolchado), el punto, el punto de cruz, el ganchillo, el bordado, la tejeduría y las alfombras. En el arte islámico, las simetrías son muy importantes en diseños como los girih persas, los azulejos zellige marroquíes, las celosías mogolas de piedra y las bóvedas decoradas con mocárabe.
La influencia directa de las matemáticas en el arte se ve en el uso de herramientas como la perspectiva, el análisis de la simetría y la presencia de objetos matemáticos en las obras, como los poliedros o la banda de Möbius. Magnus Wenninger creó poliedros estrellados coloridos, que originalmente eran modelos para enseñar.
Conceptos matemáticos como la recursión (cuando algo se repite dentro de sí mismo) y las paradojas lógicas se pueden ver en las pinturas de René Magritte y en los grabados de M. C. Escher. El arte computacional a menudo usa fractales, como el conjunto de Mandelbrot, y a veces explora otros objetos matemáticos como los autómatas celulares.
Algunos historiadores del arte, como David Hockney, han sugerido que muchos artistas desde el Renacimiento usaron herramientas ópticas como la cámara lúcida para dibujar escenas con mucha precisión. De manera similar, el arquitecto Philip Steadman ha argumentado que Johannes Vermeer usó la cámara oscura para componer sus pinturas.
Otras conexiones incluyen el análisis de obras de arte con fluorescencia de rayos X o el descubrimiento de que los batik tradicionales de la isla de Java tienen composiciones fractales. El arte a veces ha impulsado la investigación matemática, como la teoría de la perspectiva de Filippo Brunelleschi, que llevó al desarrollo de la geometría proyectiva. Una idea antigua, que viene de los Pitagóricos, es que el universo está organizado por números y que Dios es un gran geómetra. Por eso, la geometría es sagrada, como se ve en obras como El anciano de los días de William Blake.
Contenido
Orígenes: de la antigua Grecia al Renacimiento
El Canon y la simetría de Policleto
Policleto (alrededor de 450–420 a.C.) fue un escultor griego muy importante. Sus estatuas de bronce representaban principalmente a atletas. Policleto es famoso por su obra Doríforo y por la estatua de Hera. En su libro "Canon", Policleto explicó un método matemático para esculpir el cuerpo humano de forma "perfecta".
Usaba la longitud de la falange más pequeña del dedo meñique como medida básica. Multiplicaba esta longitud por la raíz cuadrada de dos (√2) para obtener la longitud de la siguiente falange, y así sucesivamente. Esta serie de medidas se usaba para formar el brazo, el pecho y todo el cuerpo.
El "Canon" de Policleto tuvo una gran influencia en la escultura de la antigua Grecia, Roma y el Renacimiento. Aunque no se conservan las obras originales de Policleto, las copias romanas muestran su ideal de perfección física y precisión matemática. Algunos creen que el pensamiento de los Pitagóricos influyó en el "Canon" de Policleto, aplicando conceptos de geometría griega como la relación, la proporción y la simetría (que en griego significa "armonía en las proporciones") para describir la forma humana.
Perspectiva y proporción
En la antigüedad, los pintores hacían las figuras más grandes o más pequeñas según su importancia en la historia, no según su distancia. En la Edad Media, algunos artistas usaron la perspectiva invertida para resaltar ciertas cosas. El matemático musulmán Alhacén (Ibn al-Haytham) describió una teoría geométrica de la óptica en su "Libro de Óptica" en 1021, pero no la aplicó al arte.
El Renacimiento trajo de vuelta las ideas clásicas griegas y romanas, incluyendo el estudio de las matemáticas para entender la naturaleza y el arte. Los artistas del Renacimiento se interesaron en las matemáticas por dos razones: primero, necesitaban saber cómo dibujar escenas tridimensionales en un lienzo plano; y segundo, creían que las matemáticas eran la esencia del mundo físico y que todo, incluyendo el arte, podía explicarse con geometría.
Los inicios de la perspectiva se vieron con Giotto (1266/7-1337), quien intentó dibujar en perspectiva. En 1415, el arquitecto italiano Filippo Brunelleschi y su amigo Leon Battista Alberti demostraron en Florencia un método geométrico para la perspectiva, usando el principio de semejanza de Euclides para calcular la altura de objetos distantes. Aunque las pinturas de Brunelleschi se perdieron, los frescos de Masaccio muestran sus principios.
El pintor italiano Paolo Uccello (1397-1475) estaba fascinado por la perspectiva, como se ve en sus pinturas de la Batalla de San Romano (c. 1435–1460), donde las lanzas rotas se alinean con las líneas de perspectiva.
El pintor Piero della Francesca (c. 1415–1492) fue un gran ejemplo de este cambio en el Renacimiento. Era artista y también un experto matemático y geómetra. Escribió libros sobre la geometría del espacio y la perspectiva, como De Prospectiva pingendi (Sobre la perspectiva para pintar).
El historiador Giorgio Vasari llamó a Piero el "geómetra más grande de su tiempo". El interés de Piero della Francesca por la perspectiva se ve en sus pinturas, como el Políptico de San Antonio. Su trabajo influyó en matemáticos y artistas posteriores, incluyendo a Luca Pacioli y Leonardo da Vinci.
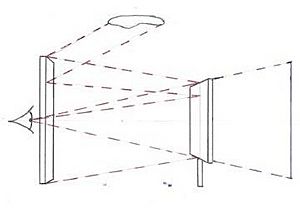
La perspectiva lineal se hizo muy popular. Alberti explicó en su libro de 1435 De pictura que: "Los rayos de luz viajan en línea recta desde los puntos de la escena hasta el ojo, formando una especie de pirámide con el ojo como la punta"'. Una pintura hecha con perspectiva lineal es como un corte de esa pirámide.
En "De Prospectiva Pingendi", Piero convirtió sus observaciones sobre cómo las figuras cambian con el punto de vista en pruebas matemáticas. Su libro se basa en el trabajo de Euclides.
En 1509, Luca Pacioli (c. 1447-1517) publicó De divina proportione, que hablaba de la relación entre las matemáticas y el arte a través de la proporción, incluso para representar el rostro humano. Leonardo da Vinci (1452–1519) ilustró el texto con grabados de sólidos regulares mientras estudiaba con Pacioli. Los dibujos de Leonardo son probablemente las primeras ilustraciones realistas de sólidos geométricos dibujados como un esqueleto de líneas gruesas.
Da Vinci estudió el libro de Pacioli y copió sus tablas de proporciones. En La Gioconda y La Última Cena, usó la perspectiva lineal con un punto de fuga para crear profundidad. La Última Cena fue diseñada con proporciones específicas, al igual que La escuela de Atenas de Rafael, que incluye a Pitágoras con tablas de proporciones ideales. En el Hombre de Vitruvio, Leonardo mostró las ideas del arquitecto romano Vitruvio, dibujando una figura masculina centrada en un círculo y un cuadrado.
Ya en el siglo XV, la perspectiva curvilínea apareció en pinturas de artistas interesados en las distorsiones. El Retrato de Giovanni Arnolfini y su esposa, de Jan van Eyck (1434), tiene un espejo convexo que refleja la escena. Parmigianino, en su Autorretrato en un espejo convexo (c. 1523–1524), muestra su cara casi sin distorsión en el centro, con un fondo muy curvo.
El espacio tridimensional también puede representarse de otras maneras, como en el dibujo técnico. Los sistemas de proyección oblicua, como la perspectiva caballera, fueron usados por artistas chinos desde el siglo I o II hasta el siglo XVIII. Los chinos aprendieron esta técnica de la India, que a su vez la aprendió de la Antigua Roma. La proyección oblicua también aparece en el arte japonés, como en las pinturas Ukiyo-e de Torii Kiyonaga (1752–1815).
-
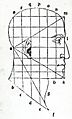
Grabado de Luca Pacioli de De divina proportione (1509) con un triángulo equilátero sobre un rostro humano.
-
Cámara lúcida en uso. Scientific American, 1879.
-
Ilustración de un artista usando una cámara oscura. Siglo XVII.
-
Teoría de la perspectiva de Filippo Brunelleschi: la Trinità de Masaccio, c. 1426–1428, en la Basílica de Santa María Novella.
-
Diagrama de Leon Battista Alberti de su obra De pictura (1435), con pilares en perspectiva sobre una cuadrícula.
-
Perspectiva de Piero della Francesca en La flagelación de Cristo, c. 1455–1460.
-
Perspectiva curvilínea: espejo curvo en el Retrato de Giovanni Arnolfini y su esposa de Jan van Eyck, 1434.
-
Parmigianino, Autorretrato en un espejo convexo, c. 1523–1524.
-
Pitágoras con una tabla de proporciones, en la La escuela de Atenas de Rafael Sanzio, 1509.
-
Proyección oblicua: Entrada y patio de un yamen. Detalle del rollo sobre la ciudad de Suzhou, obra de Xu Yang. Siglo XVIII.
-
Proyección oblicua: mujeres jugando shōgi, go y ban-sugoroku. Pintura de Torii Kiyonaga, Japón, c. 1780.
Proporción áurea
El número áureo (aproximadamente 1.618) ya era conocido por Euclides. Se ha dicho que esta proporción se usó en el arte y la arquitectura del antiguo Egipto y Grecia, pero no hay pruebas sólidas que lo demuestren.
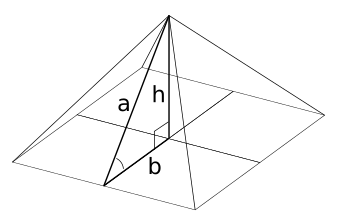
Esto podría deberse a la confusión entre la "proporción áurea" y la "media dorada", que para los griegos antiguos significaba "evitar los extremos", no una relación geométrica específica. Desde el siglo XIX, algunos han intentado encontrar la proporción áurea en el diseño de las pirámides, pero sus argumentos son dudosos. Se ha afirmado que el Partenón, un templo griego del siglo V a.C., usa la proporción áurea, pero las medidas reales no lo confirman.
También se ha dicho que la Gran Mezquita de Kairuán en Túnez usó la proporción áurea, pero no aparece en las partes originales de la mezquita. Otros estudiosos creen que, hasta el trabajo de Pacioli en 1509, la proporción áurea era desconocida para artistas y arquitectos. Después de Pacioli, la proporción áurea es más visible en obras de arte, como La Gioconda de Leonardo.
Otro número importante es el número plástico, creado en 1928 por el arquitecto holandés Hans van der Laan. Su valor es aproximadamente 1.325. Este número está relacionado con fracciones que, según el arquitecto Richard Padovan, controlan cómo percibimos los tamaños. Van der Laan usó estas proporciones al diseñar la iglesia de St. Benedictusberg Abbey (1967) en los Países Bajos.
|
[1] |
[2] |
[3] |
[4] |
|
|||
Simetrías en el plano

Las simetrías en el plano se han usado durante miles de años en alfombras, celosías, textiles y todo tipo de adornos.
Muchas alfombras tradicionales tienen un centro y un borde. Ambos pueden mostrar simetrías, aunque en las alfombras hechas a mano a menudo hay pequeñas variaciones. En los kilims de Anatolia, los motivos suelen ser simétricos. El diseño general también suele ser simétrico, con franjas o filas de motivos. Los tejedores buscaban la simetría sin conocer las matemáticas detrás de ella.
El matemático Nikos Salingaros sugiere que la belleza de una "gran alfombra" se crea usando técnicas matemáticas, como introducir colores opuestos, diferenciar áreas geométricamente, usar complejidad a pequeña escala y simetría a pequeña y gran escala, y repetir elementos en diferentes tamaños.
Las celosías elaboradas, llamadas jali, se encuentran en la India, talladas en mármol para decorar tumbas y palacios. Las celosías chinas, siempre con cierta simetría, existen en 14 de los 17 tipos de simetría plana. A menudo tienen simetría de espejo o rotacional.
Las simetrías son muy importantes en las artes textiles, como el quilting, el punto, el punto de cruz, el ganchillo, los bordados y la tejeduría. Estos patrones pueden ser solo decorativos o indicar el estatus del dueño. La simetría rotacional se encuentra en estructuras circulares como las cúpulas, a veces decoradas con patrones simétricos por dentro y por fuera, como en la Mezquita del jeque Lotf Allah de Isfahán (1619).
En el arte islámico, los patrones geométricos son muy comunes, especialmente en los azulejos girih. Estos patrones se forman con cinco tipos de baldosas: un decágono, un hexágono alargado, una "pajarita", un rombo y un pentágono. Todos los lados de estas baldosas tienen la misma longitud, y sus ángulos son múltiplos de 36°, mostrando simetrías de cinco y diez. En 2007, los físicos Peter Lu y Paul Steinhardt sugirieron que los patrones girih son similares a los cuasicristales. Los mosaicos geométricos con pequeñas piezas (zellige) son un elemento distintivo de la arquitectura de Marruecos. Las bóvedas decoradas con mocárabe son tridimensionales, pero se diseñan en dos dimensiones con dibujos de celdas geométricas.
-
Detalle de un kilim de Hotamis, Anatolia central, principios del siglo XIX.
-
Detalle de un brocado de la dinastía Ming, usando un patrón con un teselado hexagonal.
-
Celosía Jali de mármol en la tumba de Salim Chishti, Fatehpur Sikri, India.
-
Simetrías: bargello florentino.
-
Techo de la mezquita del jeque Lotf Allah, Isfahán, 1619.
-
Simetría rotacional en un encaje: encaje de bolillos.
-
Teselado girih: patrones a escalas grandes y pequeñas en una enjuta del santuario de Darb-i Imam, Isfahan, 1453.
-
Teselados: mosaicos zellige en la Madrasa de Bou Inania, Fez (Marruecos).
-
Túpac Yupanqui; túnica de Perú, 1450-1540, un textil andino que indica alto rango.
Poliedros

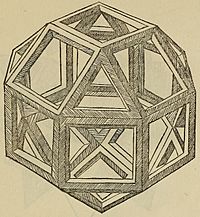
Los sólidos platónicos y otros poliedros son un tema que se repite en el arte occidental. Se encuentran, por ejemplo, en un mosaico de mármol con un pequeño dodecaedro estrellado atribuido a Paolo Uccello en la Basílica de San Marcos en Venecia. También en los diagramas de poliedros regulares de Leonardo da Vinci para el libro de Luca Pacioli De Divina Proportione (1509). Un rombicuboctaedro de cristal aparece en el retrato de Pacioli de Jacopo de' Barbari (1495). Y un poliedro truncado (y otros objetos matemáticos) aparecen en el grabado Melancolía I de Alberto Durero.
Alberto Durero (1471-1528) fue un artista alemán del Renacimiento que hizo importantes contribuciones al estudio de los poliedros en su libro de 1525, Underweysung der Messung (Educación sobre la medición). Este libro enseñaba perspectiva, geometría en arquitectura, sólidos platónicos y polígonos regulares. Durero probablemente fue influenciado por los trabajos de Piero della Francesca y Luca Pacioli en sus viajes a Italia. Su libro contiene una discusión detallada sobre los poliedros y fue el primero en mostrar cómo desplegar un poliedro para que quedara plano.
El famoso grabado de Durero Melancolía I muestra a un ser alado pensativo. La imagen incluye un cuadrado mágico y un trapezoedro triangular truncado. Estos elementos han sido muy interpretados.
Otro pintor famoso que incluyó poliedros en sus obras es el español Salvador Dalí. En su cuadro La Última Cena, Cristo y sus discípulos están dentro de un dodecaedro gigante. Otra de sus obras, la Crucifixión (1954), muestra un hipercubo desplegado, que sugiere una perspectiva divina en cuatro dimensiones.
Dimensiones fractales
Los diseños tradicionales de batik, teñidos en Indonesia, combinan motivos figurativos (como flores) con motivos abstractos y algo caóticos. Los diseños de batik tienen una dimensión fractal de entre 1 y 2, que varía según la región. Por ejemplo, el batik de Cirebon tiene una dimensión fractal de 1.1, mientras que los de Yogyakarta y Surakarta tienen entre 1.2 y 1.5.
Las obras de dripping (goteo) del artista moderno Jackson Pollock también son distintivas por su dimensión fractal. Su obra Número 14 de 1948 tiene una dimensión de 1.45, y sus pinturas posteriores tuvieron dimensiones fractales más altas, con patrones más elaborados. Una de sus últimas obras, Blue Poles, tiene una dimensión fractal de 1.72.
Una relación compleja
El astrónomo Galileo Galilei escribió que el universo "está escrito en el lenguaje de las matemáticas, y sus caracteres son triángulos, círculos y otras figuras geométricas"'. Según Galileo, los artistas que estudian la naturaleza deben primero entender las matemáticas.
Los matemáticos han intentado interpretar y analizar el arte a través de la geometría y la razón. El matemático Felipe Cucker sugiere que las matemáticas, especialmente la geometría, son una fuente de reglas para la "creación artística basada en reglas".

Las matemáticas como arte
El matemático Jerry P. King describe las matemáticas como un arte, diciendo que "las claves de las matemáticas son la belleza y la elegancia". King cita el ensayo de Godfrey Harold Hardy de 1940, Apología de un matemático, donde Hardy explica por qué encuentra hermosos dos teoremas antiguos: la prueba de Euclides de que hay infinitos números primos, y la prueba de que la raíz cuadrada de 2 es un número irracional. Hardy evalúa estos teoremas por su "sobriedad, profundidad, generalidad, imprevisibilidad, inevitabilidad" y "economía". El matemático húngaro Paul Erdős también creía que las matemáticas eran hermosas, pero pensaba que la razón iba más allá de la explicación: "¿Por qué son hermosos los números? Es como preguntar por qué es hermosa la Novena Sinfonía de Beethoven. Si no lo ves, nadie te lo puede explicar. Yo sé que los números son hermosos".
Herramientas matemáticas para el arte
Las matemáticas están presentes en casi todas las artes, como la música, la danza, la pintura, la arquitectura y la escultura.
Cada una se conecta con las matemáticas de una manera particular. Las matemáticas pueden dar herramientas a los artistas, como las reglas de la perspectiva o los métodos de geometría descriptiva, que luego se usaron para modelar objetos en computadora.
Artistas de la Edad Media y del Renacimiento (como Luca Pacioli, Leonardo da Vinci y Durero) usaron y desarrollaron ideas matemáticas mientras exploraban nuevas formas de crear arte. El uso de la perspectiva comenzó con pintores italianos como Giotto en el siglo XIII. Reglas como la del punto de fuga fueron formuladas por primera vez por Filippo Brunelleschi alrededor de 1413, e influyeron en Leonardo y Durero.
El trabajo de Isaac Newton sobre el espectro óptico influyó en la teoría de los colores de Goethe y, a su vez, en artistas como Philipp Otto Runge, J. M. W. Turner y Vasili Kandinski.
Los artistas también pueden analizar la simetría de una escena. Las mismas herramientas pueden ser usadas por matemáticos que exploran el arte, o por artistas inspirados en las matemáticas, como M. C. Escher o el arquitecto Frank Gehry, quien dijo que el diseño asistido por computadora le permitió expresarse de una manera completamente nueva.
El artista Richard Wright dice que los objetos matemáticos que se pueden construir pueden verse como "procesos para simular fenómenos" o como obras de "arte computacional". Él considera la naturaleza del pensamiento matemático, notando que los matemáticos conocían los fractales un siglo antes de que fueran reconocidos como tales.
Algunas de las primeras obras de arte computacional fueron creadas por "Drawing Machine 1", un sistema de Desmond Paul Henry que se exhibió en 1962. La máquina podía crear dibujos lineales complejos, abstractos y curvos, pero repetitivos. Más recientemente, Hamid Naderi Yeganeh ha creado formas que parecen objetos del mundo real, como peces y aves, usando fórmulas que se varían para dibujar familias de curvas. Artistas como Mikael Hvidtfeldt Christensen crean arte algorítmico escribiendo rutinas para programas de software.
-
Escultura fractal: 3D Fraktal 03/H/dd, obra de Hartmut Skerbisch, 2003.
-
Imagen de arte computacional producida por Desmond Paul Henry con su "Drawing Machine 1", exhibido en 1962.
De las matemáticas al arte

El matemático y físico teórico Henri Poincaré, autor de Ciencias e Hipótesis, fue muy leído por los cubistas, incluyendo a Pablo Picasso y a Jean Metzinger. Poincaré veía la geometría euclidiana como una de muchas formas posibles del espacio, no como una verdad absoluta. Picasso, en su obra de 1907 Las señoritas de Avignon, usó la proyección en una cuarta dimensión para mostrar figuras de frente y de perfil al mismo tiempo.
La idea de una cuarta dimensión inspiró a los artistas a cuestionar la perspectiva clásica del Renacimiento. La geometría no euclidiana se convirtió en una alternativa. El concepto de que la pintura podía expresarse matemáticamente, en color y forma, contribuyó al cubismo, el movimiento artístico que llevó al arte abstracto.
El deseo de hacer modelos para enseñar o investigar formas matemáticas crea objetos con simetrías y formas sorprendentes. Algunos de estos objetos han inspirado a artistas como los dadaistas Man Ray y Marcel Duchamp.
Man Ray fotografió algunos modelos matemáticos en el Institut Henri Poincaré en París. Notó que representaban superficies de Enneper con curvatura constante. Este fundamento matemático era importante para él, ya que le permitía decir que el objeto no era "abstracto", sino tan real como cualquier otra cosa en la naturaleza. Usó sus fotografías de los modelos matemáticos en su serie sobre las obras de William Shakespeare, como su pintura "Antony and Cleopatra" de 1934.
Escultores del siglo XX como Henry Moore, Barbara Hepworth y Naum Gabo se inspiraron en modelos matemáticos. Moore escribió sobre su Madre e hijo con cuerdas de 1938: "Me fascinaron los modelos matemáticos que vi allí... no fue el estudio científico de estos modelos, sino la capacidad de mirar a través de las cuerdas como en una jaula de pájaros y de ver una forma dentro de otra, lo que me emocionó".
Los artistas Theo van Doesburg y Piet Mondrian fundaron el movimiento De Stijl, que buscaba "establecer un vocabulario visual de formas geométricas elementales comprensibles por todos". Muchas de sus obras consisten en cuadrados y triángulos, a veces también con círculos.
Las matemáticas del teselado, los poliedros, la configuración del espacio y la autorreferencia dieron al artista gráfico M. C. Escher (1898-1972) material para sus grabados. En el Boceto de la Alhambra, Escher mostró que se puede crear arte con polígonos regulares como triángulos, cuadrados y hexágonos. También usó polígonos irregulares y a menudo usó reflejos y traslaciones para crear patrones. Muchas de sus obras contienen construcciones imposibles, que son agradables a la vista humana. Su grabado "Ascendente y Descendente" se basa en la "escalera imposible".
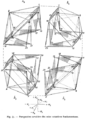
Algunos de los dibujos de teselado de Escher se inspiraron en conversaciones con el matemático Harold Scott MacDonald Coxeter sobre la geometría hiperbólica. Escher estaba especialmente interesado en cinco poliedros específicos, que aparecen muchas veces en su trabajo. Los sólidos platónicos (tetraedros, cubos, octaedros, dodecaedros e icosaedros) aparecen en "Orden y Caos" y "Cuatro Sólidos Regulares".
La complejidad visual de las estructuras matemáticas, como las teselaciones y los poliedros, ha inspirado muchas obras de arte. Stewart Coffin diseñó rompecabezas poliédricos; George W. Hart esculpió objetos inspirados en poliedros; Magnus Wenninger hizo modelos "especialmente hermosos" de poliedros estrellados complejos.
Las perspectivas distorsionadas con efectos de anamorfosis se han explorado en el arte desde el siglo XVI, cuando Hans Holbein el Joven incluyó una calavera muy distorsionada en su pintura "Los embajadores" de 1533.
Las matemáticas de la topología han inspirado a varios artistas modernos. El escultor John Robinson (1935-2007) creó obras como Gordian Knot y Bands of Friendship, mostrando la teoría de nudos en bronce pulido.
Otros trabajos de Robinson exploran la topología de figuras toroidales. Su obra Genesis se basa en un nudo borromeo, un conjunto de tres aros entrelazados. El escultor Helaman Ferguson creó complejas superficies y otros objetos topológicos. Sus obras son representaciones visuales de objetos matemáticos. La escultora Bathsheba Grossman también basó su trabajo en estructuras matemáticas.
Un proyecto de investigación explora las conexiones entre las matemáticas y el arte a través de la banda de Möbius, flexágonos, origamis y fotografías panorámicas.
Objetos matemáticos, como el Atractor de Lorenz y el plano hiperbólico, se han creado usando el arte del tejido, incluyendo el ganchillo. La tejedora estadounidense Ada Dietz escribió un libro en 1949 que definía patrones de tejido basados en la expansión de polinomios.
El matemático J. C. P. Miller usó el autómata celular Rule 90 para diseñar tapices que representaban árboles y patrones abstractos de triángulos. Los "mathekniticians" Pat Ashforth y Steve Plummer usaron versiones tejidas de objetos matemáticos como flexágonos para sus clases.
-
Anamorfismo: Los embajadores, obra de Hans Holbein el Joven, 1533, con una calavera fuertemente distorsionada.
-
Cuarta dimensión en el cubismo: Esprit Jouffret, 1903. Tratado elemental de geometría en cuatro dimensiones.
-
Retrato de Pablo Ruiz Picasso, por Juan Gris. Proyección de un modelo tridimensional en facetas planas superpuestas.
-
Movimiento de De Stijl: Composition I (Still Life), obra de Theo van Doesburg de 1916.
-
Una banda de Möbius, en forma de bufanda de ganchillo, 2007.
-
Pedagogía y arte: Magnus Wenninger con algunos de sus poliedros estrellados, 2009.
Ilustrando matemáticas
| Tríptico Stefaneschi de Giotto (1320), ejemplo de recursión. A la derecha, detalle con el Cardenal Stefaneschi sujetando el tríptico completo. | |

El Tríptico Stefaneschi de Giotto (1320) muestra la recursión (algo que se repite dentro de sí mismo). El panel central del tríptico tiene la figura del cardenal Stefaneschi arrodillado, sosteniendo el tríptico completo. Las pinturas metafísicas de Giorgio de Chirico, como su "Gran Interior metafísico" de 1917, exploran los niveles de representación en el arte al incluir pinturas dentro de sus propias pinturas.
El arte puede mostrar paradojas lógicas, como algunas pinturas del surrealista René Magritte. En La condition humaine (1933), Magritte pinta un caballete con un paisaje a través de una ventana, enmarcado por cortinas "reales" en la pintura. De manera similar, Print Gallery de Escher (1956) muestra una ciudad distorsionada que contiene una galería donde aparece la propia imagen, y así ad infinitum. Magritte usó esferas y cuboides para distorsionar la realidad, pintándolos junto a casas como si fueran bloques de construcción gigantes.
El cuadro de Salvador Dalí, La cola de golondrina (1983), fue parte de una serie inspirada en la teoría de las catástrofes de René Thom. El pintor y escultor español Pablo Palazuelo (1916-2007) se centró en la investigación de la forma. Desarrolló un estilo que describió como la geometría de la vida y la geometría de toda la naturaleza, usando formas geométricas simples con patrones y colores detallados.
El artista Adrian Gray creó el equilibrio de rocas, jugando con la fricción y el centro de masas para crear composiciones sorprendentes y aparentemente imposibles.
Los artistas no siempre toman las propiedades de la geometría de forma literal. Como Douglas Hofstadter escribió en su libro Gödel, Escher, Bach: un Eterno y Grácil Bucle, la diferencia entre un dibujo de Escher y la geometría no euclidiana es que en esta última, se pueden encontrar interpretaciones comprensibles, mientras que en el arte de Escher, el resultado final no se puede reconciliar con nuestra propia idea del mundo. Hofstadter habla de la litografía "Print Gallery" de M. C. Escher, que muestra una ciudad costera que contiene una galería de arte que parece contener una pintura de la ciudad costera, creando un "bucle extraño".
Análisis de la historia del arte
El análisis de imágenes de obras de arte, por ejemplo, usando fluorescencia de rayos X, puede revelar información sobre el arte. Estas técnicas pueden descubrir imágenes debajo de capas de pintura, ayudar a los historiadores del arte a ver una obra antes de que se deteriore, o distinguir una copia de un original.

El estilo de dripping ("goteo") de Jackson Pollock tiene una dimensión fractal definida. Entre los artistas que pudieron influir en el caos controlado de Pollock, Max Ernst pintó curvas de Lissajous directamente balanceando un cubo de pintura agujereado sobre un lienzo.
El científico informático Neil Dodgson investigó si las pinturas de rayas de Bridget Riley podían caracterizarse matemáticamente. Concluyó que, aunque la distancia de separación y la entropía global podían "proporcionar cierta caracterización", la correlación no era concluyente porque sus patrones eran irregulares.
La medida estética del matemático estadounidense George David Birkhoff, publicada en 1933, propone una forma de medir la calidad estética de una obra de arte. No intenta medir el significado de una pintura, sino que se limita a los "elementos de orden" de una figura poligonal. Combina cinco parámetros: si tiene un eje vertical de simetría, si hay equilibrio óptico, cuántas simetrías rotacionales tiene, cómo es el fondo y si hay características insatisfactorias. Esta medida, O, toma un valor entre −3 y 7. La segunda medida, C, considera los elementos de la figura. Luego, define la medida estética de la belleza de un objeto como "O/C". Esto se puede interpretar como un equilibrio entre el placer de ver el objeto y el esfuerzo necesario para entenderlo.
Los estímulos a la investigación matemática
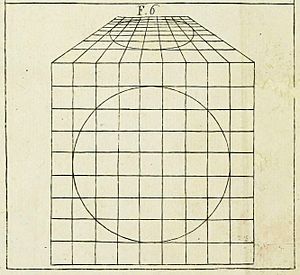
El arte a veces ha impulsado el desarrollo de las matemáticas. Por ejemplo, la teoría de Brunelleschi sobre la arquitectura y la pintura llevó al trabajo de Brook Taylor y Johann Heinrich Lambert sobre los fundamentos matemáticos del dibujo en perspectiva, y finalmente a la geometría proyectiva de Girard Desargues y Jean-Victor Poncelet.
El arte japonés de plegado de papel, el origami, ha sido estudiado matemáticamente por Tomoko Fuse. A partir de piezas de papel iguales, como cuadrados, analiza las operaciones necesarias para convertirlas en poliedros o teselas. Esta técnica fue usada en 1893 por T. Sundara Rao en sus "Ejercicios geométricos de plegado de papel" para demostraciones geométricas. Las matemáticas del origami se han explorado en el teorema de Maekawa, el teorema de Kawasaki y los axiomas de Huzita–Hatori.
Ilusiones ópticas y Op-art
Las ilusiones ópticas como la espiral de Fraser muestran las limitaciones de nuestra percepción visual, creando lo que el historiador del arte Ernst Gombrich llamó un "truco desconcertante". Las líneas en blanco y negro que parecen espirales son en realidad círculos concéntricos. El estilo de las pinturas y gráficos del movimiento Op-art de mediados del siglo XX usó estos efectos para crear la impresión de movimiento y patrones vibrantes, como en el trabajo de artistas como Bridget Riley y Victor Vasarely.
Geometría sagrada
Una corriente del arte, desde la antigua Grecia, ve a Dios como el geómetra del mundo, y la geometría del mundo, por lo tanto, como sagrada. La creencia de que Dios creó el universo según un plan geométrico es muy antigua. Plutarco atribuyó esta creencia a Platón, escribiendo que "Platón dijo que Dios geometriza continuamente". Esta idea ha influido en el pensamiento occidental desde entonces. El concepto platónico viene de la idea pitagórica de armonía en la música, donde las notas estaban espaciadas en proporciones perfectas. Los pitagóricos creían que todo estaba organizado por el Número. De la misma manera, en el pensamiento platónico, los sólidos platónicos (los cinco poliedros regulares convexos) dictan las proporciones que se encuentran en la naturaleza y en el arte.
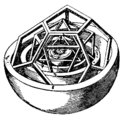
En 1596, el astrónomo y matemático Johannes Kepler modeló el universo como un conjunto de sólidos platónicos anidados, determinando los tamaños relativos de las órbitas de los planetas. Dos pinturas de William Blake, Ancient of Days e Isaac Newton, intentan representar el contraste entre el mundo espiritual matemáticamente perfecto y el mundo físico imperfecto. Salvador Dalí, en su obra de 1954 Crucifixión, visualiza la cruz como un hipercubo, que representa la perspectiva divina con cuatro dimensiones. En otra de sus obras, La Última Cena (1955), Cristo y sus discípulos están dentro de un gran dodecaedro gigante.
-
Sólidos platónicos encajados, modelo de los planetas en el sistema solar incluido en el Mysterium Cosmographicum de Johannes Kepler, 1596.
-
The Ancient of Days, obra de William Blake, 1794.
-
Símbolos masónicos: Dios como el supremo arquitecto.
Galería de imágenes
-
Matemáticas en el arte: grabado en placa de cobre de Alberto Durero Melancolía I, 1514. Las referencias matemáticas incluyen una brújula para la geometría, un cuadrado mágico y un romboedro truncado, mientras que la medición está indicada por las escalas y el reloj de arena.
-
Dibujo alámbrico de un vaso como sólido de revolución, obra de Paolo Uccello. Siglo XV.
Véase también
 En inglés: Mathematics and art Facts for Kids
En inglés: Mathematics and art Facts for Kids
- Arquitectura y matemáticas
- Música y matemáticas