Geometría hiperbólica para niños
La geometría hiperbólica es un tipo de geometría que es diferente a la que normalmente aprendemos en la escuela, la geometría euclidiana. Imagina que la geometría euclidiana es como dibujar en una hoja de papel plana. La geometría hiperbólica, en cambio, es como dibujar en una superficie con forma de silla de montar o de patata frita.
Aunque se parece mucho a la geometría euclidiana y comparte muchos de sus principios, la geometría hiperbólica no sigue una de las reglas más famosas de Euclides: el quinto postulado de Euclides sobre las líneas paralelas.
Para entenderlo mejor, piensa en la curvatura de una superficie:
- La geometría euclidiana tiene una curvatura plana, es decir, curvatura cero.
- La geometría hiperbólica tiene una curvatura negativa, como una silla de montar.
- La geometría elíptica (otro tipo de geometría) tiene una curvatura positiva, como la superficie de una esfera.
Contenido
Historia de la geometría hiperbólica
¿Cómo se descubrió la geometría hiperbólica?
Desde hace mucho tiempo, los matemáticos intentaron demostrar que el quinto postulado de Euclides (la regla de las paralelas) podía deducirse de los otros cuatro.
Los primeros intentos
En el siglo XVIII, un matemático llamado Giovanni Gerolamo Saccheri hizo un gran esfuerzo. Sin darse cuenta, sus estudios lo llevaron a crear las bases de lo que hoy conocemos como geometría hiperbólica. Sin embargo, él pensó que sus resultados no eran correctos y no continuó con su trabajo.
Otro matemático, Johann Heinrich Lambert, también encontró cosas interesantes. Descubrió que en los triángulos de esta nueva geometría, la suma de sus ángulos siempre es menor de 180 grados. En la geometría euclidiana, la suma de los ángulos de un triángulo siempre es exactamente 180 grados.
Los matemáticos que la publicaron
Más tarde, Carl Friedrich Gauss también investigó algo parecido, pero no publicó sus descubrimientos. Finalmente, en la década de 1820, dos jóvenes matemáticos, János Bolyai y Nikolai Ivanovich Lobachevsky, trabajando por separado, publicaron sus ideas. Ellos demostraron que era posible tener una geometría diferente y totalmente lógica, que es la que hoy llamamos geometría hiperbólica.
Introducción a la geometría hiperbólica
¿Cómo son las líneas paralelas en geometría hiperbólica?
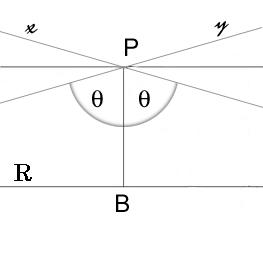
En la geometría euclidiana, el quinto postulado de Euclides dice que si tienes una línea recta r y un punto P fuera de ella, solo hay una línea que pasa por P y que nunca se cruza con r. A esa línea la llamamos "paralela".
En la geometría hiperbólica, esta regla cambia. Si tienes una línea r y un punto P fuera de ella, ¡hay al menos dos líneas diferentes que pasan por P y que no se cruzan con r! De hecho, hay infinitas.
Tipos de líneas que no se cruzan
En la geometría hiperbólica, hay dos tipos de líneas que no se cruzan con otra línea r desde un punto P:
- Líneas hiperparalelas: Son las líneas que se acercan mucho a la línea r a medida que te alejas infinitamente, pero nunca la tocan. Hay exactamente dos de estas líneas que pasan por P.
- Líneas ultraparalelas: Son las líneas que también pasan por P y no se cruzan con r, pero la distancia entre ellas no se hace más pequeña a medida que te alejas. Hay un número infinito de estas líneas.
Entonces, el postulado de las paralelas en geometría hiperbólica se podría decir así: "En geometría hiperbólica, dada una línea r y un punto P fuera de r, hay exactamente dos líneas que pasan por P que son hiperparalelas a r, e infinitas líneas que pasan por P que son ultraparalelas a r".
El ángulo de paralelismo
En la geometría euclidiana, el ángulo que forma una línea paralela con una línea perpendicular a la original es siempre de 90 grados. En la geometría hiperbólica, este ángulo cambia. Depende de la distancia entre el punto P y la línea r. Cuanto más cerca esté P de r, más se parecerá el ángulo a 90 grados. Cuanto más lejos esté P, el ángulo se acercará a cero.
Esto significa que, a distancias muy pequeñas, la geometría hiperbólica se parece mucho a la geometría euclidiana. Por eso, si vivieras en un plano hiperbólico, te costaría darte cuenta de que no estás en un plano euclidiano si solo observas cosas pequeñas.
Recuerda que en la geometría euclidiana, la suma de los ángulos de cualquier triángulo es 180 grados. En la geometría hiperbólica, esta suma siempre es menor de 180 grados. La diferencia es mayor cuanto más grande es el área del triángulo.
¿Cómo se relaciona la geometría hiperbólica con nuestro mundo?
Es posible que la geometría hiperbólica sea la verdadera geometría de nuestro universo a una escala muy grande, a nivel del cosmos. Sin embargo, si fuera así, la diferencia entre la suma de los ángulos de un triángulo y 180 grados sería tan, tan pequeña que la geometría euclidiana seguiría siendo una excelente aproximación para cualquier cosa que observemos en nuestra vida diaria.
Modelos para entender la geometría hiperbólica
Para ayudarnos a entender la geometría hiperbólica, los matemáticos han creado "modelos" que la representan en un espacio euclidiano. Los más conocidos son el modelo de Klein y el modelo de Poincaré. Curiosamente, estos modelos fueron propuestos por Eugenio Beltrami en 1868, pero se hicieron famosos gracias a Felix Klein y Henri Poincaré.
El modelo de Klein
También conocido como el modelo del disco proyectivo, usa el interior de un círculo como si fuera el plano hiperbólico. Las líneas rectas en este modelo son las cuerdas de ese círculo. Su ventaja es que es simple, pero las formas hiperbólicas se ven un poco distorsionadas.
El modelo de Poincaré
Este modelo también usa el interior de un círculo. Aquí, las líneas rectas de la geometría hiperbólica se representan como arcos de circunferencia que cortan el borde del círculo en ángulo recto. Este modelo es muy útil para visualizar cómo se comportan las líneas y las formas en la geometría hiperbólica.
Véase también
 En inglés: Hyperbolic geometry Facts for Kids
En inglés: Hyperbolic geometry Facts for Kids
- Geometría euclídea
- Geometría elíptica
- Geometría no euclídea
- Nikolái Lobachevski