Poliedro para niños
Un poliedro es una figura geométrica tridimensional. Sus caras son planas y encierran un espacio limitado. La palabra "poliedro" viene del griego antiguo polyedron. Significa "muchas bases" o "muchas caras".
Los poliedros son formas en tres dimensiones. Pero existen ideas similares en otras dimensiones. Por ejemplo, un punto es como un poliedro de cero dimensiones. Una línea es como uno de una dimensión. Un polígono es como uno de dos dimensiones. Y un polícoro es como uno de cuatro dimensiones. Todas estas formas se llaman politopos. Así, un poliedro es un politopo tridimensional.
Contenido
¿Qué es un poliedro?
La forma más común de entender un poliedro es como una parte del espacio. Esta parte está cerrada por polígonos planos.
La definición de poliedro puede cambiar. A veces se refiere al volumen que ocupa. Otras veces, a los polígonos que lo forman. O solo a las líneas que crean su esqueleto.
¿Cómo se nombran los poliedros?
El nombre de un poliedro nos dice algo sobre él. Depende de sus características importantes.
Generalmente, el nombre incluye:
- Una cualidad de sus caras. Puede ser el número de caras (como tetraedro con 4, pentaedro con 5). O su forma (como deltaedro si son triangulares).
- Propiedades especiales del poliedro. Por ejemplo, si es regular o toroidal.
- Cambios que se le han hecho. Como si está truncado (cortado) o estrellado.
¿Cómo se clasifican los poliedros?
Los poliedros se pueden organizar de varias maneras. Aquí te mostramos algunas:
- Los poliedros convexos son aquellos que no tienen "huecos" hacia adentro. Si unes dos puntos dentro de ellos, la línea siempre queda dentro. Si la línea se sale, se llaman poliedros cóncavos.
- Los poliedros de caras regulares solo tienen polígonos regulares como caras. Un polígono regular tiene todos sus lados y ángulos iguales.
- Los poliedros isoedrales tienen todas sus caras iguales.
- Los poliedros isotoxales tienen todas sus aristas (bordes) iguales.
- Los poliedros isogonales tienen todos sus vértices (esquinas) iguales.
Estas características nos ayudan a agrupar los poliedros en familias:
| Convexos | Caras regulares | Caras iguales | Aristas iguales | Vértices iguales | Familia |
|---|---|---|---|---|---|
| Sí | Sí | No | No | No | Sólidos de Johnson |
| No siempre | Sí | No | Sí | Sí | Poliedros cuasirregulares |
| No siempre | Sí | No siempre | No siempre | Sí | Poliedros uniformes |
| No siempre | No siempre | Sí | No siempre | Sí | Poliedros nobles |
| No siempre | Sí | Sí | Sí | Sí | Poliedros regulares |
| No | Sí | Sí | Sí | Sí | Sólidos de Kepler-Poinsot |
| Sí | Sí | Sí | Sí | Sí | Sólidos platónicos |
Nombres de poliedros según sus caras
El nombre de un poliedro a menudo nos dice cuántas caras tiene. Se usa un prefijo que indica el número, seguido de "-edro". Por ejemplo:
| Nombre | Número de caras |
|---|---|
| Tetraedro | 4 |
| Pentaedro | 5 |
| Hexaedro | 6 |
| Octaedro | 8 |
| Dodecaedro | 12 |
| Icosaedro | 20 |
| Triacontaedro | 30 |
| Hectaedro | 100 |
| Chiliaedro | 1.000 |
| Miriaedro | 10.000 |
| Apeiroedro | infinitos |
Familias de poliedros
Poliedros regulares
Un poliedro regular tiene todas sus caras, aristas y vértices iguales. Sus caras son polígonos regulares. Hay nueve poliedros regulares en total. Cinco son convexos, llamados sólidos platónicos. Los otros cuatro no son convexos y se llaman sólidos de Kepler-Poinsot.
Sólidos platónicos
Los sólidos platónicos son poliedros regulares y convexos. Solo existen cinco:
| Nombre | Imagen |
|---|---|
| Tetraedro |  |
| Cubo o hexaedro regular |  |
| Octaedro |  |
| Dodecaedro |  |
| Icosaedro |  |
Sólidos de Kepler-Poinsot
Los sólidos de Kepler-Poinsot son poliedros regulares que no son convexos. Hay cuatro de ellos. Se forman a partir del dodecaedro o del icosaedro.
| Nombre | Imagen |
|---|---|
| Gran dodecaedro |  |
| Pequeño dodecaedro estrellado |  |
| Gran icosaedro |  |
| Gran dodecaedro estrellado |  |
Poliedros irregulares
Los poliedros irregulares tienen caras, aristas o vértices que no son todos iguales.
Sólidos arquimedianos
Los sólidos arquimedianos son poliedros convexos y uniformes. Esto significa que sus vértices son todos iguales. Pero sus caras no son todas iguales. Hay trece sólidos arquimedianos. Algunos se pueden obtener "cortando" las esquinas de los sólidos platónicos.
| Nombre | Imagen |
|---|---|
| Tetraedro truncado |  |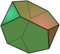
| Cuboctaedro |  |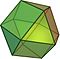
| Cubo truncado |  |
| Octaedro truncado |  |
| Rombicuboctaedro |  |
| Cuboctaedro truncado |  |
| Cubo romo |  |
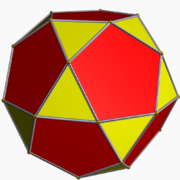
| Icosidodecaedro |  |
| Dodecaedro truncado |  |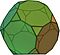
| Icosaedro truncado |  |
| Rombicosidodecaedro |  |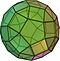
| Icosidodecaedro truncado |  |
| Dodecaedro romo |  |
Prismas y antiprismas
Los prismas y antiprismas son otras familias de poliedros. Hay un número infinito de ellos.
Los prismas tienen dos caras paralelas (llamadas bases) y caras laterales que son cuadrados. Por ejemplo, un prisma triangular tiene dos triángulos y tres cuadrados.
Los antiprismas también tienen dos bases. Pero sus caras laterales son triángulos.
Sólidos de Johnson
Los sólidos de Johnson son poliedros convexos con caras regulares. Pero no son uniformes. Hay 92 sólidos de Johnson.
Otras familias de poliedros
Sólidos de Catalan
Los sólidos de Catalan son los "duales" de los sólidos de Arquímedes. Ser "dual" significa que las caras de uno son los vértices del otro, y viceversa. Por ejemplo, el dual del icosaedro (20 caras, 12 vértices) es el dodecaedro (12 caras, 20 vértices). Los sólidos de Catalan tienen todas sus caras iguales, pero no son polígonos regulares.
| Nombre | Imagen |
|---|---|
| Tetraedro triakis |  |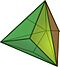
| Dodecaedro rómbico |  |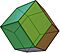
| Triaquisoctaedro |  |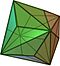
| Tetraquishexaedro |  |
| Icositetraedro deltoidal |  |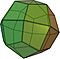
| Disdiaquisdodecaedro |  |
| Icositetraedro pentagonal |  |
| Triacontaedro rómbico | |
| Triaquisicosaedro |  |
| Pentaquisdodecaedro |  |
| Hexacontaedro deltoidal |  |
| Disdiaquistriacontaedro |  |
| Hexecontaedro pentagonal |  |
Deltaedros
Los deltaedros son cuerpos formados solo por triángulos equiláteros (triángulos con todos sus lados iguales). Hay ocho deltaedros convexos. Tres son sólidos platónicos: el tetraedro, el octaedro y el icosaedro. Los otros cinco son sólidos de Johnson.
| Nombre | Imagen |
|---|---|
| Tetraedro |  |
| Octaedro | |
| Icosaedro |  |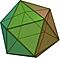
| Bipirámide triangular |  |
| Bipirámide pentagonal |  |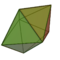
| Biesfenoide romo | |
| Prisma triangular triaumentado |  |
| Bipirámide cuadrada giroelongada |  |
Trapezoedros
Los trapezoedros son los duales de los antiprismas.
Poliedros infinitos
También existen poliedros con un número infinito de caras. Se llaman apeiroedros. Algunos ejemplos son:
- Las teselados o teselaciones. Son poliedros que cubren completamente una superficie plana.
- Los poliedros oblicuos infinitos.
Poliedros en otros espacios
El concepto de poliedro también se puede aplicar a otros tipos de espacios:
- Un poliedro esférico es como una teselación en la superficie de una esfera.
- También es posible crear teselaciones en un espacio hiperbólico.
Galería de imágenes
-
Triaquistetraedro
-
Dodecaedro rómbico
-
Triaquisoctaedro
-
Tetraquishexaedro
-
Icositetraedro deltoidal
-
Disdiaquisdodecaedro
-
Icositetraedro pentagonal
-
Triacontaedro rómbico
-
Triaquisicosaedro
-
Pentaquisdodecaedro
-
Hexecontaedro deltoidal
-
Disdiaquistriacontaedro
-
Hexecontaedro pentagonal
Véase también
En inglés: Polyhedron Facts for Kids
