Triángulo equilátero para niños
Datos para niños Triángulo equilátero |
||
|---|---|---|
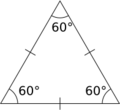
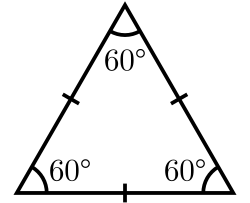 Tres lados iguales y sus tres ángulos son de 60°
|
||
| Características | ||
| Lados | 3 | |
| Vértices | 3 | |
| Grupo de simetría | 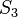 |
|
| Símbolo de Schläfli | {3/1} | |
| Diagrama de Coxeter-Dynkin | ||
| Polígono dual | Triángulo equilátero | |
| Área |
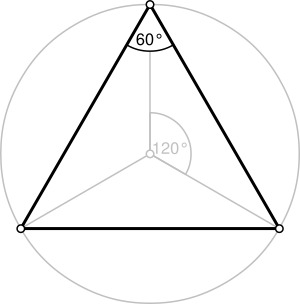
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tfrac{\sqrt{3</td></tr><tr><td class="noprint" colspan="3" style="text-align:left;"></td></tr></table><!--IB_END-->{4} a^2 | ángulo = 60° | propiedades de = Convexo En geometría, un triángulo equilátero es una figura con tres lados que miden lo mismo. También tiene sus tres ángulos internos iguales. Cada uno de estos ángulos mide 60 grados. Los triángulos equiláteros son un tipo especial de polígono regular, lo que significa que todos sus lados y ángulos son idénticos. Contenido¿Qué hace especial a un triángulo equilátero?Un triángulo equilátero tiene características muy interesantes que lo hacen único. Simetría y puntos importantesLos triángulos equiláteros son muy simétricos. Tienen 3 líneas de simetría. Cada una de estas líneas pasa por un vértice (una esquina) y el punto medio del lado opuesto. Debido a esta simetría, varias líneas y puntos importantes dentro del triángulo coinciden:
Todos estos elementos se encuentran en el mismo lugar. Esto significa que el ortocentro, el baricentro, el incentro y el circuncentro (que son puntos especiales en cualquier triángulo) se unen en un solo punto central en el triángulo equilátero. Rotación y semejanzaSi giras un triángulo equilátero 0°, 120° o 240° alrededor de su centro, la figura se verá exactamente igual. Esto muestra su alta simetría. Además, todos los triángulos equiláteros son "semejantes". Esto significa que, aunque puedan ser de diferentes tamaños, tienen la misma forma. Si agrandas o encoges un triángulo equilátero, seguirá siendo un triángulo equilátero. Medida de los ángulos
Fórmulas importantes del triángulo equiláteroAquí te mostramos algunas fórmulas para calcular medidas de un triángulo equilátero, usando 'a' para la longitud de uno de sus lados:
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p = 3 \cdot a
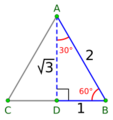
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): h = a \cdot \frac{\sqrt{3}}{2} * Puedes calcularla usando el teorema de Pitágoras en la mitad del triángulo.
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = a^2 \cdot \frac{\sqrt{3}}{4} * También puedes calcular el área si conoces la altura: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = h^2 \cdot \frac{\sqrt{3}}{3} Radios de circunferenciasUn triángulo equilátero puede tener varias circunferencias relacionadas con él:
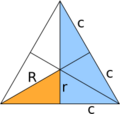
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): R = a \cdot \frac{\sqrt{3}}{3}
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): r = a \cdot \frac{\sqrt{3}}{6} * Una curiosidad es que el radio de la circunferencia circunscrita (R) es el doble del radio de la circunferencia inscrita (r), es decir, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): R = 2 \cdot r . ¿Cómo se construyen los triángulos equiláteros?Los triángulos equiláteros son figuras básicas en geometría y se usan para construir otras formas más complejas. Por ejemplo:
Uso en la historiaLos triángulos equiláteros han sido importantes desde hace mucho tiempo. Por ejemplo, se han encontrado construcciones basadas en triángulos equiláteros en el yacimiento prehistórico de Lepenski Vir, en Serbia. Esto demuestra que las personas ya usaban estas formas geométricas hace miles de años. Para saber más
Galería de imágenesVéase también
|
|




 En inglés:
En inglés: