Geometría proyectiva para niños
La geometría proyectiva es una rama de las matemáticas que estudia las propiedades de incidencia de las figuras geométricas. Esto significa que se enfoca en cómo los puntos y las líneas se conectan entre sí, sin importar las distancias o los ángulos. Es como si miraras un objeto desde un punto fijo y vieras cómo se proyecta en una superficie, sin preocuparte por su tamaño real. A veces, esta palabra también se usa para hablar de la geometría descriptiva, que es la teoría de la proyección.
Contenido
¿Cómo Nació la Geometría Proyectiva?
La geometría proyectiva comenzó gracias a Gérard Desargues en el siglo XVII. Él sentó las bases matemáticas para los métodos de perspectiva que los artistas del Renacimiento usaban en sus pinturas. Imagina cómo los artistas hacían que los objetos lejanos parecieran más pequeños y las líneas paralelas parecieran unirse en el horizonte. Desargues explicó esto con matemáticas.
Aunque su trabajo se publicó en 1639, no fue muy conocido por casi doscientos años. Fue en el siglo XIX cuando la geometría proyectiva y otras nuevas geometrías se hicieron más importantes en las matemáticas. A principios del siglo XX, científicos como Albert Einstein usaron estas nuevas geometrías para entender mejor el universo a gran escala, mostrando que eran muy útiles.
Principios Básicos de la Geometría Proyectiva
Desde un punto de vista sencillo, la geometría proyectiva se basa en algunas ideas clave:
- Dos puntos siempre forman una línea recta.
- Todas las líneas se cruzan en un punto. Esto es un poco diferente a lo que aprendemos normalmente. En la geometría proyectiva, incluso las líneas que parecen paralelas (como las vías del tren) se encuentran en un punto muy, muy lejano, al que llamamos "punto del infinito".
Estos principios son simétricos. Esto significa que si en un teorema (una afirmación matemática que se puede demostrar) cambias la palabra "línea" por "punto" y "punto" por "línea", obtendrás otro teorema que también es cierto. A esto se le llama el principio de dualidad, y fue descubierto por Jean-Victor Poncelet en el siglo XIX.
La geometría proyectiva se llama una geometría de incidencia porque se centra en cómo los elementos (puntos, líneas) se "inciden" o se encuentran, sin usar medidas de distancia o ángulo.
¿Para Qué Sirve la Geometría Proyectiva?
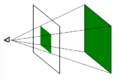
La geometría proyectiva es muy útil porque nos permite entender cómo se ven los objetos cuando los observamos desde un punto específico. Piensa en cómo una fotografía captura una escena: las líneas paralelas en la vida real pueden parecer que se juntan en la foto. La geometría proyectiva explica esto.
También es una herramienta poderosa para simplificar muchos teoremas de la geometría euclidiana (la geometría que aprendemos en la escuela, con distancias y ángulos). Aunque no puede demostrar cosas que la geometría euclidiana no pueda, a menudo hace que las demostraciones sean más sencillas y claras.
Imagina que estás dibujando un paisaje. Las líneas que en la realidad son paralelas (como los bordes de una carretera recta) parecen unirse en el horizonte. La geometría proyectiva nos ayuda a entender y dibujar esto correctamente. Es como la matemática detrás de la perspectiva en el arte y el diseño.
¿Cómo se Describe la Geometría Proyectiva con Números?
La geometría proyectiva también se puede describir usando números y vectores, aunque de una manera un poco diferente a la geometría normal. En lugar de pensar en puntos con coordenadas exactas (como (x,y)), pensamos en "direcciones".
Imagina que tienes un punto en el espacio. Desde tu ojo, todos los puntos que están en la misma línea que pasa por tu ojo y por ese punto, se ven como si fueran el mismo punto. La geometría proyectiva captura esta idea.
Para representar estos "puntos proyectivos" se usan las coordenadas homogéneas. Son como coordenadas normales, pero con una regla especial: si multiplicas todas las coordenadas por el mismo número (que no sea cero), sigues representando el mismo punto proyectivo. Por ejemplo, (1:2:3) y (2:4:6) representan el mismo punto en geometría proyectiva. Esto es porque lo que importa no son los valores exactos, sino la proporción entre ellos.
Galería de imágenes
-
La luz del objeto llega al ojo del observador, pasando por el plano del dibujo. La geometría proyectiva analiza esto matemáticamente, estudiando las propiedades de incidencia.
Véase también
En inglés: Projection (mathematics) Facts for Kids
- Geometría
- Geometría descriptiva
- Geometría finita
- Plano proyectivo
