Recursión para niños

La recursión o recursividad es una idea fascinante que significa que algo puede contenerse o aplicarse a sí mismo una y otra vez. Imagina una muñeca rusa que tiene dentro una muñeca más pequeña, y esa otra más pequeña, y así sucesivamente. Eso es recursión.
En términos más sencillos, la recursión ocurre cuando un problema grande se divide en versiones más pequeñas del mismo problema. Para resolver el problema grande, solo necesitas saber cómo resolver las versiones más pequeñas. Siempre hay un punto de partida muy simple, llamado "caso base", que no necesita más divisiones.
Por ejemplo:
- El Factorial: Si quieres calcular el factorial de un número (como 5!, que es 5x4x3x2x1), puedes pensarlo de forma recursiva. El factorial de 5 es 5 multiplicado por el factorial de 4. El factorial de 4 es 4 multiplicado por el factorial de 3, y así. El "caso base" es el factorial de 0, que siempre es 1.
- Ordenar por Fusión: Imagina que tienes una lista muy larga de números desordenados y quieres ordenarlos. Puedes dividir la lista en dos mitades. Luego, ordenas cada mitad por separado (usando el mismo método de división). Una vez que las dos mitades están ordenadas, las juntas de nuevo. El "caso base" es cuando tienes una lista con cero o un número, ¡esa lista ya está ordenada!
En estos ejemplos, un problema se divide en partes más pequeñas del mismo tipo, hasta que llegas a una parte tan simple que ya sabes la respuesta.
Contenido
Recursión en las Matemáticas
La recursión es muy importante en las matemáticas para definir conjuntos y funciones.
Números que se Construyen a Sí Mismos
Un buen ejemplo de un conjunto definido de forma recursiva son los números naturales (0, 1, 2, 3, ...):
- El número 0 pertenece a los números naturales.
- Si un número n pertenece a los números naturales, entonces n+1 también pertenece a los números naturales.
- Cualquier otro número que cumpla estas dos reglas también es un número natural.
Funciones que se Definen a Sí Mismas
Muchas funciones matemáticas se pueden definir usando recursión.
Un ejemplo muy conocido es la función factorial n!, que ya mencionamos:
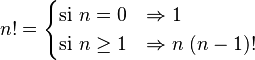
Veamos cómo se usa esta definición para encontrar el factorial de 3: 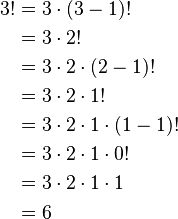
Otros ejemplos de funciones y secuencias matemáticas definidas de forma recursiva son:
- Sucesión de Fibonacci — donde cada número es la suma de los dos anteriores (por ejemplo, 0, 1, 1, 2, 3, 5, 8...).
Recursión en la Informática y Programación
En la programación de computadoras, la recursión es una herramienta muy útil. A menudo, para resolver un problema complicado, los programadores lo dividen en problemas más pequeños del mismo tipo. Esta técnica se llama "divide y vencerás".
¿Cómo se ve la Recursión en el Código?
Aquí te mostramos cómo se vería la función factorial escrita en diferentes lenguajes de programación. Verás que la idea es la misma: si el número es mayor que 1, la función se llama a sí misma con un número más pequeño. Si es 0 o 1, devuelve 1 (el caso base).
Implementación en C:
int factorial (int n)
{
if (n > 1)
{
return n * factorial(n-1); // La función se llama a sí misma
}else
{
return 1; // Caso base
}
}
int main()
{
printf("Recursividad\n");
int result = factorial(5);
printf("El resultado es: %i", result);
return 0;
}Implementación en C++:
int factorial(int x)
{
if (x > -1 && x < 2) return 1; // Cuando -1 < x < 2 devolvemos 1 (0! = 1 y 1! = 1)
else if (x < 0) return 0; // Error: no existe factorial de números negativos
return x * factorial(x - 1); // Si x >= 2, la función se llama a sí misma
}Implementación en Pascal:
FUNCTION Factorial (CONST N: INTEGER): INTEGER;
BEGIN
IF N > 1 THEN
Factorial := N * (Factorial (N - 1)); // La función se llama a sí misma
ELSE
BEGIN
IF ((N=0) OR (N=1))
Factorial := 1; // Caso base
ELSE
Factorial := 0; // Manejo de error para números negativos
END;
END;
END;Implementación en Python:
def factorial(n):
if n == 1 or n == 0:
return 1 # Caso base
else:
return n * factorial(n-1) # La función se llama a sí mismaPara entender mejor cómo funciona la recursión en la programación, veamos el ejemplo del factorial de 3:
- Queremos calcular 3!
- La función `factorial(3)` se llama. Como 3 es mayor que 1, devuelve `3 * factorial(2)`.
- Ahora, la función `factorial(2)` se llama. Como 2 es mayor que 1, devuelve `2 * factorial(1)`.
- Finalmente, la función `factorial(1)` se llama. Como 1 es el caso base, devuelve `1`.
- Ahora, las llamadas anteriores se resuelven en orden inverso:
* `factorial(2)` recibe el `1` de `factorial(1)`, así que calcula `2 * 1 = 2`. * `factorial(3)` recibe el `2` de `factorial(2)`, así que calcula `3 * 2 = 6`.
- El resultado final es 6.
Recursión en el Humor
La recursión se usa a menudo para hacer chistes o juegos de palabras, especialmente en el mundo de la informática, la filosofía o las matemáticas. Por ejemplo, en un glosario de un libro, podrías encontrar una entrada como esta:
- Recursividad, véase Recursividad.
Si buscas la palabra "recursión" en el buscador Google, a veces te sugiere: «Quizá quisiste decir: recursión».
Un chiste común en informática dice: «Lo primero para entender la recursividad, es entender la recursividad». También es común que algunos programas o proyectos tengan nombres que son acrónimos recursivos. Por ejemplo:
- PHP significa PHP Hypertext Preprocessor (Preprocesador de Hipertexto PHP).
- WINE significa WINE Is Not an Emulator (WINE no es un emulador).
- GNU significa GNU's Not Unix (GNU no es Unix).
Véase también
 En inglés: Recursion Facts for Kids
En inglés: Recursion Facts for Kids
- Algoritmo recursivo
- Fractal
- Torres de Hanói
- Iteración


