Autómata celular para niños
Un autómata celular (A.C.) es como un modelo matemático o un juego de simulación. Imagina una cuadrícula gigante, como un tablero de ajedrez, donde cada casilla (llamada "célula") puede cambiar de estado. Estas células interactúan entre sí siguiendo reglas sencillas.
Los autómatas celulares son útiles para entender cómo funcionan sistemas complejos en la naturaleza. Por ejemplo, cómo se forman los copos de nieve o cómo se mueven las multitudes. Evolucionan paso a paso, como si el tiempo avanzara en pequeños saltos.
Contenido
¿Qué es un autómata celular?
Un autómata celular es un sistema dinámico. Esto significa que sus partes cambian con el tiempo. Está formado por una rejilla de celdas. Cada celda puede estar en un estado específico, como "encendida" o "apagada", o tener un color. El estado de una celda cambia según reglas que dependen de sus vecinas.
Elementos clave de un autómata celular
Para entender un autómata celular, necesitamos conocer sus partes principales:
- Espacio regular: Es la cuadrícula donde viven las células. Puede ser una línea, un plano (como una hoja de papel) o un espacio con más dimensiones. Cada división de este espacio es una célula.
- Conjunto de estados: Son los posibles valores que una célula puede tener. Por ejemplo, "vivo" o "muerto", o diferentes colores. Este conjunto es siempre limitado.
- Configuración inicial: Es cómo empiezan todas las células. Es decir, el estado que tiene cada célula al principio.
- Vecindades: Son las células que están cerca de una célula específica. La "vecindad" define qué células influyen en el cambio de estado de una célula.
- Función de transición local: Es la regla que decide cómo cambia el estado de una célula. Esta regla se basa en el estado actual de la célula y en el estado de sus vecinas. Es como una instrucción que dice: "Si tú y tus vecinas están así, entonces tú cambias a este otro estado".
Tipos de vecindades comunes
En los autómatas celulares de dos dimensiones, hay dos tipos de vecindades muy usadas:
- Vecindad de Von Neumann: Considera las 4 células que están justo arriba, abajo, a la izquierda y a la derecha de la célula central.
- Vecindad de Moore: Incluye las 8 células que rodean a la célula central. Es decir, las 4 de Von Neumann más las 4 de las esquinas.
¿Cómo se comportan los autómatas celulares?
Los autómatas celulares pueden mostrar comportamientos muy diferentes. Se clasifican en cuatro clases principales:
- Clase I: El sistema siempre termina en un estado uniforme y estable. Es como si todas las células se pusieran de acuerdo para tener el mismo estado.
- Clase II: Se forman patrones que se repiten o estructuras simples. Los cambios iniciales solo afectan a una pequeña zona.
- Clase III: Los patrones evolucionan de forma impredecible y caótica. Un pequeño cambio al principio puede afectar a todo el sistema.
- Clase IV: Se crean estructuras complejas y sorprendentes. Combinan patrones que se repiten con un comportamiento impredecible.
Historia de los autómatas celulares
Los autómatas celulares fueron pensados por primera vez en la década de 1940.
La era de Von Neumann
John von Neumann, un científico muy importante, trabajó en la década de 1950 en la idea de máquinas que pudieran construirse a sí mismas. Con la ayuda de su amigo Stanislaw Ulam, aplicó esta idea a los autómatas celulares. Usaron una cuadrícula de dos dimensiones y reglas para que las células cambiaran de estado.
La era de John Horton Conway
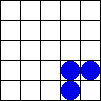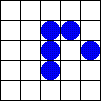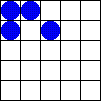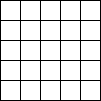
En 1970, John Horton Conway creó el autómata celular más famoso: el Juego de la vida. Este juego se hizo muy popular. Se juega en una cuadrícula donde las células pueden estar "vivas" o "muertas". Las reglas son muy sencillas:
- Nacimiento: Una célula muerta "nace" (se vuelve viva) si tiene exactamente 3 vecinas vivas.
- Muerte: Una célula viva "muere" si tiene menos de 2 vecinas vivas (por soledad) o más de 3 vecinas vivas (por sobrepoblación).
- Supervivencia: Una célula viva sigue viva si tiene 2 o 3 vecinas vivas.
El Juego de la vida puede crear patrones muy complejos y sorprendentes.
La era de Stephen Wolfram
Stephen Wolfram investigó mucho sobre cómo se comportan los autómatas celulares. Clasificó sus comportamientos en las cuatro clases que mencionamos antes (Clase I, II, III y IV). Su trabajo ayudó a entender mejor la complejidad que puede surgir de reglas simples.
¿Para qué sirven los autómatas celulares?
Los autómatas celulares son herramientas muy útiles para simular y entender muchos sistemas en el mundo real. Aquí tienes algunos ejemplos:
- Tráfico: Pueden simular cómo se mueven los coches en una carretera o las personas en una multitud.
- Fluidos: Ayudan a entender cómo se comportan los líquidos y los gases.
- Biología: Se usan para modelar el crecimiento de células o la propagación de ciertos virus.
- Computación: Sirven para diseñar cómo las computadoras procesan información de forma paralela.
- Redes neuronales: Se usan para crear modelos de redes que aprenden y reconocen patrones.
- Desastres naturales: Pueden simular incendios forestales para ayudar a prevenirlos o combatirlos.
- Materiales: Se utilizan para estudiar cómo cambian las estructuras de los metales, como en la soldadura o la fabricación.
Ejemplos de autómatas celulares
Autómata celular de una dimensión
Este es el tipo más simple. Las células están en una línea y solo pueden tener dos estados, como "0" o "1". Cada célula solo mira a sus dos vecinas más cercanas para decidir su próximo estado. Hay 256 reglas diferentes para este tipo de autómatas.
Juego de la vida
Como ya mencionamos, este es el autómata celular más conocido. Fue creado por John Horton Conway en 1970. Sus reglas sencillas sobre el nacimiento, la muerte y la supervivencia de las células crean patrones muy interesantes y complejos.
La hormiga de Langton
Creada por Christopher Langton en 1986, esta simulación tiene una "hormiga" que se mueve sobre un plano de baldosas blancas y negras. La hormiga sigue estas reglas:
- Cambia el color de la baldosa donde está.
- Gira 90 grados: a la derecha si la baldosa era blanca, a la izquierda si era negra.
- Avanza a la siguiente baldosa.
Al principio, la hormiga se mueve de forma simple, luego caótica, y finalmente forma un camino diagonal que se repite.
Lenia
Lenia es un autómata celular más reciente. Es una versión más avanzada y general del Juego de la vida de Conway, que permite crear patrones aún más diversos y complejos.
Ventajas y Desventajas
Ventajas de los autómatas celulares
1. Simplicidad: Aunque sus reglas son simples, pueden crear comportamientos muy complejos. 2. Escalabilidad: Se pueden simular en computadoras de forma muy eficiente, incluso para sistemas muy grandes. 3. Flexibilidad: Se usan en muchos campos, como la física, la biología y la informática. 4. Visualización: Es fácil ver cómo evolucionan y se forman los patrones, lo que ayuda a entenderlos.
Desventajas de los autómatas celulares
1. Sensibilidad: A veces, un pequeño cambio en las reglas o en el inicio puede cambiar mucho el resultado final. 2. Interpretación: Entender los patrones complejos que surgen puede ser difícil. 3. Limitaciones: No siempre son los mejores para modelar sistemas muy específicos con reglas muy complicadas. 4. Recursos: Algunos autómatas celulares requieren mucha capacidad de computadora, especialmente si son muy grandes o complejos.
Galería de imágenes
-
El caparazón de Conus textile muestra un patrón caracterizable en términos de autómatas celulares.
Véase también
 En inglés: Cellular automaton Facts for Kids
En inglés: Cellular automaton Facts for Kids
- Autómata celular cuántico
- Emergencia (filosofía)
- Máquina de Turing
- Teoría de autómatas
- Ciudad Permutación
- Lenia
- Regla 184
- Gusanos de Paterson