Toro (geometría) para niños
.gif)
Toro de anillo (como una rosquilla)
Toro de cuerno (sin agujero central)
Toro de huso (con un agujero muy pequeño)
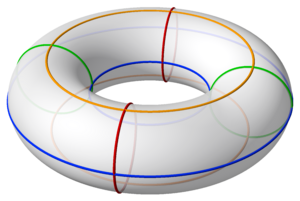
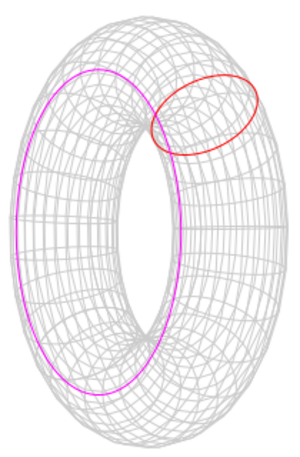
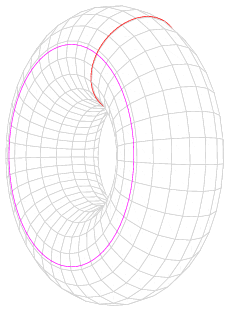
En geometría, un toro es una forma especial que parece una rosquilla o un flotador. Imagina un círculo que gira alrededor de una línea recta que no lo toca. La superficie que se forma es un toro.
La palabra "toro" viene del latín torus, que significa "protuberancia" o "elevación curva". En la antigüedad, ya se usaba para describir objetos con esta forma, como algunas molduras en la arquitectura. Muchos objetos que usamos a diario tienen forma de toro, como las rosquillas o las cámaras de aire de los neumáticos.
Contenido
¿Qué es un Toro en Geometría?
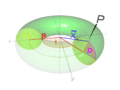
Un toro se puede describir con números y fórmulas. Piensa en él como un objeto en el espacio tridimensional. Para entender su forma, necesitamos dos medidas importantes:
- R: Es la distancia desde el centro del toro hasta el centro del "tubo" que lo forma. Imagina el centro de la rosquilla.
- r: Es el radio del "tubo" o "anillo" del toro. Es como el grosor de la rosquilla.
Para que sea un toro con agujero (como una rosquilla), el radio grande (R) debe ser mayor que el radio pequeño (r).
¿Cómo se calcula su tamaño?
Podemos calcular la superficie (el área de su "piel") y el volumen (cuánto espacio ocupa) de un toro usando fórmulas especiales:
- Superficie (A):
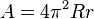
- Volumen (V):
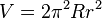
Aquí, 
(pi) es un número especial que usamos en matemáticas, aproximadamente 3.14159.
El Toro en la Topología
En topología, que es una rama de las matemáticas que estudia las formas y cómo se conectan, el toro es muy importante. Se le conoce como la "superficie cerrada orientable de género 1". Esto significa que es una superficie sin bordes y que tiene un solo "agujero".
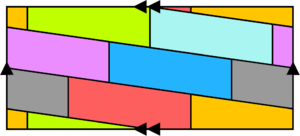
Imagina que tienes un rectángulo de papel. Si pegas los bordes de arriba y abajo para formar un cilindro, y luego pegas los extremos de ese cilindro, ¡obtienes un toro! Esto nos ayuda a entender cómo se conectan sus partes.
El Toro Plano
Un "toro plano" es un tipo especial de toro que, aunque parece una rosquilla, es "plano" en el sentido de que su superficie no tiene curvas hacia afuera o hacia adentro en ningún punto. Es como si pudieras estirar una hoja de papel y doblarla para formar un cilindro sin arrugarla. Luego, si pudieras doblar ese cilindro para formar un toro sin estirar el papel, tendrías un toro plano.
En nuestro mundo de tres dimensiones, no podemos hacer un toro plano perfecto sin estirar o arrugar el material. Sin embargo, en dimensiones más altas (como cuatro dimensiones), sí es posible.
El Toro en Más Dimensiones
Podemos imaginar toros en más de tres dimensiones. Un "toro n-dimensional" es como un toro normal, pero extendido a más dimensiones.
- Un "1-toro" es simplemente un círculo.
- El toro que conocemos (como una rosquilla) es un "2-toro".
- Un "3-toro" sería como un toro normal, pero con una dimensión extra.
Estos toros de más dimensiones son muy útiles en matemáticas avanzadas y en física.
Usos y Aplicaciones del Toro
En Matemáticas
El toro es un objeto de estudio fascinante. Por ejemplo, el famoso "teorema de los cuatro colores" dice que cualquier mapa en un plano se puede colorear con solo cuatro colores sin que dos regiones vecinas tengan el mismo color. Pero si dibujamos un mapa en la superficie de un toro, ¡necesitamos hasta siete colores! Esto demuestra que la forma del espacio cambia las reglas.
En Física
El toro es muy importante en la física, especialmente en el estudio de la energía.
- Imanes: Para crear imanes potentes, a veces se enrolla un cable alrededor de un toro. Al pasar electricidad, se genera un campo magnético dentro del toro.
- Fusión Nuclear: Algunos de los sistemas más avanzados para generar energía limpia, como los tokamaks, usan una forma toroidal para contener el plasma a temperaturas extremadamente altas. Esto ayuda a controlar la fusión nuclear.
- Aceleradores de Partículas: Muchos aceleradores de partículas también tienen una forma parecida a un toro para guiar las partículas a velocidades muy altas.
En Óptica
En el campo de la óptica, las lentes tóricas se usan para corregir el astigmatismo, un problema de la vista. Estas lentes tienen una superficie con dos curvaturas diferentes en direcciones perpendiculares, lo que les da una forma similar a una parte de un toro.
En Videojuegos
En muchos videojuegos de estrategia o de mundo abierto, los personajes pueden viajar hacia el norte y reaparecer por el sur, o ir hacia el este y salir por el oeste. Esto crea la ilusión de un mundo esférico, pero en realidad, el mapa del juego está diseñado como un plano rectangular cuyos bordes opuestos están "conectados", ¡como si fuera la superficie de un toro! A esto se le llama a veces "mundo toroide".
Galería de imágenes
-
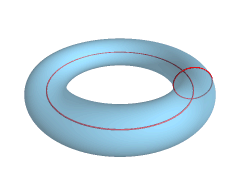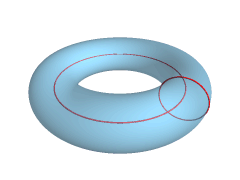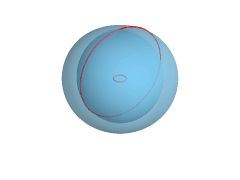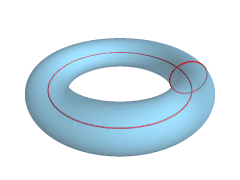
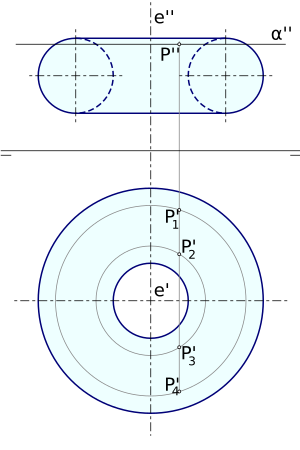
Intersección de un toro y un plano.
-
Animación de un toro cortado por un plano, y creación de Círculos de Villarceau.
-
Ilustración de un toro con sus principales variables.
-
Una geodésica cerrada del toro.
Véase también
En inglés: Torus Facts for Kids
