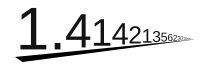Raíz cuadrada de dos para niños
La raíz cuadrada de 2 es un número muy interesante en matemáticas. Imagina un número que, cuando lo multiplicas por sí mismo, el resultado es exactamente 2. Ese número es la raíz cuadrada de 2. Se escribe con el símbolo 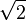 o también como
o también como 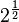 .
.
Lo que hace a la raíz cuadrada de 2 muy especial es que es un número irracional. Esto significa que su valor decimal es infinito y nunca se repite en un patrón. Por ejemplo, su valor aproximado es 1,41421356237... y sigue y sigue sin fin.
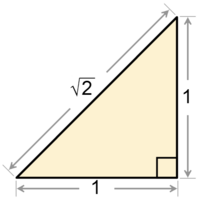
Geométricamente, la raíz cuadrada de 2 es la longitud de la diagonal de un cuadrado que tiene lados de 1 unidad de largo. Puedes comprobar esto usando el famoso teorema de Pitágoras. Por eso, a veces se le llama la constante pitagórica.
La raíz cuadrada de 2 no se puede escribir como una fracción simple (un número entero dividido por otro número entero). Sin embargo, es la solución de una ecuación matemática sencilla:
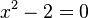
Este número aparece en muchos lugares de nuestra vida diaria:
- Las hojas de papel de tamaño internacional (ISO 216), como las que usamos en la escuela, tienen una proporción de largo a ancho igual a la raíz cuadrada de 2. Esto es útil porque si doblas una hoja por la mitad, la nueva hoja mantiene la misma proporción.
- En la música, la relación de frecuencias en algunos intervalos musicales, como la cuarta aumentada, es la raíz cuadrada de 2.
- En la electricidad, la tensión máxima de la corriente alterna es la raíz cuadrada de 2 veces el valor que normalmente se indica (como 110 o 220 voltios).
- En la fotografía, los valores de apertura del diafragma de una cámara siguen una secuencia basada en la raíz cuadrada de 2.
Contenido
Historia de la raíz cuadrada de 2
La raíz cuadrada de 2 fue probablemente el primer número irracional que se conoció.
Antiguas aproximaciones
Hace mucho tiempo, en la antigua Babilonia (alrededor del 2000 al 1650 a.C.), ya se conocía una aproximación de la raíz cuadrada de 2. Una tablilla babilónica llamada YBC 7289 muestra un valor muy cercano, que es como tener seis decimales correctos.
También en la antigua India, en un texto matemático llamado Baudhaiana-sulba-sutra (entre el 600 y el 300 a.C.), se describe una forma de calcular una aproximación de este número.
El descubrimiento de los números irracionales
El descubrimiento de que la raíz cuadrada de 2 no se podía expresar como una fracción simple se atribuye a un matemático pitagórico llamado Hipaso de Metaponto. Se dice que Hipaso demostró que este número era irracional usando la geometría.
En aquella época, los pitagóricos creían que todos los números podían expresarse como una relación entre dos números enteros. La idea de un número irracional, que no podía ser una fracción, fue muy sorprendente y generó mucha discusión.
Más tarde, el matemático griego Teeteto (417 a.C. - 369 a.C.) estudió problemas que también llevaban a la aparición de la raíz cuadrada de 2.
¿Cómo se calcula la raíz cuadrada de 2?
Existen varios métodos para encontrar una aproximación de la raíz cuadrada de 2. Uno de los más comunes, usado en computadoras y calculadoras, es el llamado método babilónico.
Funciona así: 1. Eliges un número inicial cualquiera, digamos 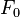 . No importa mucho cuál elijas, solo es un punto de partida. 2. Luego, usas una fórmula para mejorar tu aproximación. La fórmula es: :
. No importa mucho cuál elijas, solo es un punto de partida. 2. Luego, usas una fórmula para mejorar tu aproximación. La fórmula es: :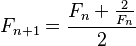 . Cuantas más veces repitas este cálculo, más cerca estarás del valor real de la raíz cuadrada de 2.
. Cuantas más veces repitas este cálculo, más cerca estarás del valor real de la raíz cuadrada de 2.
En 1997, un equipo liderado por Yasumasa Kanada calculó la raíz cuadrada de 2 con más de 137 mil millones de decimales. ¡Es una cantidad enorme de números!
¿Por qué es un número irracional?
Existen varias formas de demostrar que la raíz cuadrada de 2 es un número irracional. Una de las pruebas más conocidas se basa en suponer que sí es un número racional (una fracción) y luego demostrar que esa suposición lleva a una contradicción. Esto significa que la suposición inicial debe ser falsa, y por lo tanto, la raíz cuadrada de 2 no puede ser racional.
Prueba con argumentos de números pares e impares
Una forma de entender por qué es irracional es la siguiente:
- Imagina que la raíz cuadrada de 2 sí se puede escribir como una fracción
 , donde
, donde 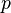 y
y 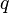 son números enteros y la fracción ya no se puede simplificar más.
son números enteros y la fracción ya no se puede simplificar más. - Si elevas al cuadrado ambos lados de la ecuación
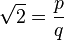 , obtienes
, obtienes 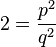 , lo que significa Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2q^2 = p^2 .
, lo que significa Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2q^2 = p^2 . - Esto nos dice que
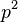 es un número par. Si
es un número par. Si 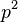 es par, entonces
es par, entonces 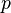 también debe ser par (porque si
también debe ser par (porque si 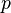 fuera impar,
fuera impar, 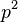 también sería impar).
también sería impar). - Como
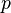 es par, podemos escribirlo como
es par, podemos escribirlo como 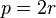 (donde
(donde  es otro número entero).
es otro número entero). - Ahora, sustituimos
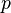 en la ecuación original: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2q^2 = (2r)^2 , lo que simplifica a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2q^2 = 4r^2 , y luego a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): q^2 = 2r^2 .
en la ecuación original: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2q^2 = (2r)^2 , lo que simplifica a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2q^2 = 4r^2 , y luego a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): q^2 = 2r^2 . - Esto significa que
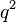 también es un número par. Y si
también es un número par. Y si 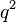 es par, entonces
es par, entonces 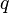 también debe ser par.
también debe ser par. - ¡Aquí está la contradicción! Si
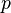 es par y
es par y 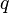 es par, entonces la fracción original
es par, entonces la fracción original  se podría simplificar (dividiendo ambos por 2). Pero habíamos dicho al principio que la fracción no se podía simplificar.
se podría simplificar (dividiendo ambos por 2). Pero habíamos dicho al principio que la fracción no se podía simplificar. - Como llegamos a una contradicción, nuestra suposición inicial de que la raíz cuadrada de 2 es una fracción debe ser falsa. Por lo tanto, es un número irracional.
Propiedades de la raíz cuadrada de dos
La mitad de la raíz cuadrada de 2 es aproximadamente 0,707106781... Este número es muy útil en geometría y trigonometría. Por ejemplo, el vector unitario que forma un ángulo de 45° con los ejes de un plano tiene coordenadas (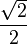 ,
, 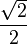 ).
).
También se cumple que:
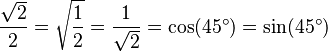 .
.
Una propiedad curiosa de la raíz cuadrada de 2 es esta:
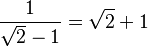 .
.
Este resultado está relacionado con la razón plateada, otra constante matemática interesante.
La raíz cuadrada de 2 también se puede representar como una fracción continua infinita:
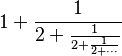 .
.
La raíz cuadrada de 2 en diferentes sistemas numéricos
El valor de la raíz cuadrada de 2 se puede expresar de diferentes maneras según el sistema de numeración:
- En binario: 1,0110101000001001111...
- En decimal: 1,4142135623730950488...
- En Hexadecimal: 1,6A09E667F3BCC908B2F...
Usos en la geometría euclidiana
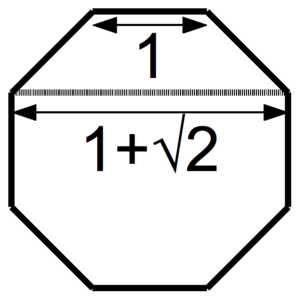
La raíz cuadrada de 2 aparece en el estudio de varias figuras geométricas:
- En el cuadrado.
- En el octógono regular.
- En el triángulo rectángulo isósceles.
- En la fórmula del volumen de un tetraedro regular.
Datos curiosos
- En 2006, Shigeru Kondo usó una computadora durante más de 13 días para calcular la raíz cuadrada de 2 con doscientos mil millones de decimales. ¡Si quisieras imprimir todos esos números, necesitarías 100 millones de hojas de papel!
- Puedes "ver" la raíz cuadrada de 2 en la vida real: en un día soleado, coloca una varilla verticalmente en el suelo. Cuando la sombra de la varilla tenga exactamente la misma longitud que la varilla, une la punta de la sombra con la parte superior de la varilla con una cuerda. La longitud de esa cuerda será igual a la raíz cuadrada de 2.
Véase también
 En inglés: Square root of 2 Facts for Kids
En inglés: Square root of 2 Facts for Kids
- La raíz cuadrada de 2 es la cociente de aspecto de los Formato de papeles bajo ISO 216.
- Raíz cuadrada de 3
- Raíz cuadrada de 5