Teselado para niños

Los teselados son patrones de figuras geométricas que cubren completamente una superficie plana. Imagina que estás colocando baldosas en el suelo: para que sea un teselado, las baldosas deben cumplir dos reglas importantes:

1. No deben dejar ningún espacio entre ellas.
2. No deben superponerse, es decir, no pueden estar una encima de la otra.

Los teselados se crean usando copias idénticas de una o varias figuras, llamadas teselas. Estas copias se mueven y giran sin cambiar su tamaño ni forma, como si fueran piezas de un rompecabezas que encajan perfectamente para cubrir toda la superficie.

A lo largo de la historia, muchas culturas han usado esta técnica para decorar suelos y paredes con mosaicos en edificios importantes.

• Hace miles de años, los sumerios ya hacían mosaicos con patrones geométricos.
• En el siglo III antes de Cristo, el sabio Arquímedes estudió qué figuras geométricas regulares podían cubrir un plano sin dejar huecos.
• Johannes Kepler, un astrónomo alemán, también investigó esto en su libro Harmonice mundi en 1619.
• Más tarde, entre 1869 y 1891, matemáticos y científicos como Camille Jordan y Evgenii Konstantinovitch Fiodorov estudiaron a fondo las simetrías de los teselados.
• Un artista muy famoso por sus teselados es el neerlandés M. C. Escher (1898-1972). Él se inspiró en los diseños del palacio de La Alhambra en Granada para crear obras de arte increíbles y llenas de misterio.

Ángulos que comparten un vértice

Tipos de Teselados

Existen diferentes tipos de teselados, dependiendo de las figuras que se usen para crearlos.

Teselados Regulares

Un teselado regular es aquel que usa un solo tipo de polígono regular (una figura con todos sus lados y ángulos iguales) para cubrir el plano. Estos diseños se han usado mucho para decorar desde hace mucho tiempo.

• 

  Triángulos equiláteros

• 

  Cuadrados

• 

  Hexágonos

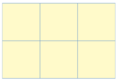
Por ejemplo, los cuadrados tienen ángulos de 90 grados. Si colocas cuatro cuadrados juntos, sus esquinas se unen en un punto y suman 360 grados, cubriendo perfectamente el espacio alrededor de ese punto.

Teselados Semirregulares

Los teselados semirregulares se forman con dos o más tipos de polígonos regulares.

Tienen estas características:

• Solo usan polígonos regulares.
• La forma en que los polígonos se unen es la misma en cada punto donde se encuentran sus esquinas (vértices).
• Solo existen ocho tipos de teselados semirregulares.

• 

  4 8 8

• 

  3 3 3 4 4

• 

  3 3 4 3 4

• 

  3 3 3 3 6

• 

  3 12 12

• 

  3 4 6 4

• 

  3 6 3 6

• 

  4 6 12

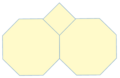
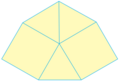
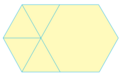
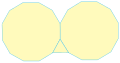
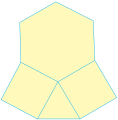
Ejemplos de teselados semirregulares

• 

  4 8 8

• 

  3 3 4 3 4

• 

  3 3 3 3 6

• 

  3 12 12

• 

  3 4 6 4

• 

  3 6 3 6

• 

  4 6 12

Teselados Irregulares

Estos teselados se forman con polígonos que no son regulares, pero aun así cubren la superficie sin dejar espacios.

Teselados con Cuadriláteros

Cualquier paralelogramo (una figura de cuatro lados con lados opuestos paralelos) puede formar un teselado. Solo necesitas copiarlo y colocarlo uno al lado del otro.

De hecho, cualquier figura de cuatro lados (cuadrilátero), ya sea cóncava o convexa, puede cubrir una superficie plana.

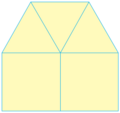
Teselados con Triángulos

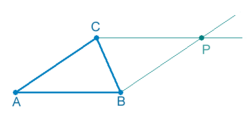
Cualquier triángulo puede cubrir todo el plano. Puedes comprobarlo formando un paralelogramo con dos triángulos iguales y luego copiando ese paralelogramo.

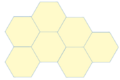
Teselados con Hexágonos

Además de los hexágonos regulares, algunos hexágonos no regulares que tienen simetría central también pueden formar teselados.

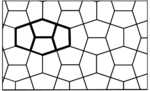
Teselado de El Cairo

Teselado de El Cairo, Egipto.

Este teselado es muy común en las calles de El Cairo, Egipto, y en el arte islámico. Se forma con una figura de cinco lados (pentágono) que tiene dos ángulos rectos, un ángulo de 144° y dos ángulos de 108°.

Polígonos Cóncavos

Algunas figuras con formas más complejas y "hundidas" (cóncavas) también pueden teselar.

• 

  Flecha derecha

• 

  Cruz griega

• 

  Ángulo himterk

• 

  Flecha de pestaña

Cómo se Construyen los Teselados

Una forma de construir teselados es usando un método llamado "Resta, suma y rota en 180°".

Método "Resta, suma y rota en 180°"

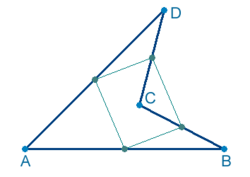
Primero, dibujas una figura simple que ya pueda teselar por sí misma, como un paralelogramo o un triángulo. Luego, le quitas una parte de un lado y la añades exactamente igual al lado opuesto. Después, copias esta nueva figura y la vas colocando para que encaje perfectamente, usando movimientos como la traslación (mover), la rotación (girar) y la simetría (reflejar).

Isometría

Las transformaciones isométricas son movimientos en el plano que no cambian el tamaño ni la forma de una figura. Usando estas transformaciones, se pueden crear muchos diseños diferentes de teselados.

Notación de Teselados

Para identificar los diferentes tipos de teselados, se usa una forma especial de escribirlos, creada por A. P. Rollett y Henry Martyn Cundy. Se enumeran los lados de los polígonos que se unen en cada vértice, siguiendo el sentido de las agujas del reloj y separándolos con puntos.

Por ejemplo:

• Para un teselado de triángulos equiláteros, donde seis triángulos se unen en cada vértice, se escribe 3.3.3.3.3.3.
• Para cuadrados, donde cuatro se unen en cada vértice, es 4.4.4.4.
• Para hexágonos, donde tres se unen, es 6.6.6.

Para que sea más corto, si el mismo polígono se repite varias veces en un vértice, se usa un número pequeño arriba (superíndice) para indicar cuántas veces. Así, los ejemplos anteriores se convierten en 3⁶, 4⁴ y 6³. Esta notación se usa tanto para teselados regulares como para semirregulares.

Mallas de Doble Capa

Las mallas de doble capa son estructuras que tienen sus puntos de unión (nudos) en dos niveles o superficies, que suelen ser paralelas. Estos nudos se conectan con barras.

Cada una de las capas de una malla de doble capa puede verse como un teselado. Así, una malla de doble capa es como una combinación de tres teselados: uno para la capa de abajo, uno para la capa de arriba y otro para las barras que los conectan en diagonal.

Galería de imágenes

• 

  Teselado en el pavimento de una calle

• 

  Teselado hexagonal decorando un suelo (Roma)

• 

  Ejemplo de pavimento teselado natural en la península de Tasman, Tasmania, Australia.

Véase también

En inglés: Tessellation Facts for Kids