Conjunto de Mandelbrot para niños
El conjunto de Mandelbrot es una de las figuras más famosas y estudiadas en el mundo de las fractales. Recibe su nombre en honor al matemático Benoît Mandelbrot (1924-2010), quien lo investigó en la década de 1970.
Imagina que tienes un plano especial donde cada punto es un "número complejo". Estos números son un poco diferentes a los que usas normalmente, ya que tienen una parte "real" y una parte "imaginaria". El conjunto de Mandelbrot se forma siguiendo una regla matemática muy sencilla para cada uno de esos puntos.
La regla funciona así: 1. Empiezas con el número cero. 2. Luego, tomas ese número, lo elevas al cuadrado y le sumas el punto del plano que estás probando (llamémoslo c). 3. El resultado lo vuelves a elevar al cuadrado y le sumas c otra vez. 4. Repites este proceso muchas veces.
Si los números que obtienes en esta secuencia se mantienen "controlados" (es decir, no se hacen infinitamente grandes), entonces el punto c pertenece al conjunto de Mandelbrot. Si los números se disparan y se hacen enormes, entonces c no pertenece al conjunto.
Por ejemplo:
- Si c = 1, la secuencia sería: 0, 1, 2, 5, 26, ... Como ves, los números crecen muy rápido. Por eso, el 1 no es parte del conjunto de Mandelbrot.
- Si c = –1, la secuencia sería: 0, –1, 0, –1, ... Estos números se mantienen pequeños y repetitivos. Por lo tanto, el –1 sí pertenece al conjunto de Mandelbrot.
Para dibujar el conjunto de Mandelbrot, se usa un método llamado "algoritmo de tiempo de escape". Los puntos que no pertenecen al conjunto se colorean según la rapidez con la que sus secuencias se hacen grandes. Los colores más oscuros suelen indicar que la secuencia se disparó rápidamente, mientras que los colores más claros significan que tardó más en crecer.
Se sabe que si en algún momento de la secuencia un número se aleja más de 2 unidades del centro del plano, ese punto c definitivamente no pertenece al conjunto. Esto ayuda a los ordenadores a saber cuándo parar de calcular.
Contenido
Historia del Conjunto de Mandelbrot
La idea de repetir funciones matemáticas para crear patrones ya existía desde principios del siglo XX, gracias a matemáticos como Gaston Julia y Pierre Fatou. Sin embargo, la verdadera belleza y complejidad de estas figuras no se pudo ver hasta que los ordenadores fueron lo suficientemente potentes.
Las primeras imágenes del conjunto de Mandelbrot, aunque un poco básicas, fueron creadas en 1978 por Robert Brooks y Peter Matelski.
Benoit Mandelbrot fue quien realmente popularizó este conjunto en un artículo de 1980, despertando el interés de científicos de todo el mundo.
Más tarde, los matemáticos Adrien Douady y John H. Hubbard estudiaron a fondo el conjunto, demostraron muchas de sus propiedades y le dieron el nombre en honor a Mandelbrot. Ellos descubrieron que el conjunto de Mandelbrot está "conectado", es decir, no tiene partes separadas.
Desde entonces, muchos otros matemáticos han contribuido a entender mejor este fascinante conjunto.
¿Cómo se ve el Conjunto de Mandelbrot?
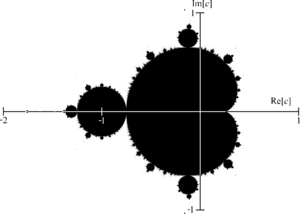
El conjunto de Mandelbrot es una forma negra en el centro de las imágenes. A su alrededor, se ven colores que cambian según la rapidez con la que los puntos "escapan" del conjunto.
Propiedades Visuales del Conjunto de Mandelbrot
Una de las características más asombrosas de los fractales es que, si amplías una parte de ellos, ¡puedes encontrar patrones muy parecidos a la imagen original! Es como si la misma forma se repitiera una y otra vez, a diferentes escalas.
Mira estas ampliaciones:
-
Recuadro verde
-
Minirecuadro gris
-
Recuadro blanco
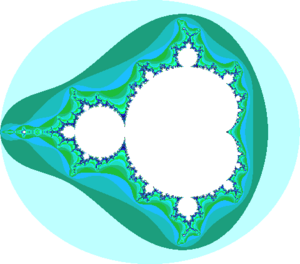
- Si amplías el recuadro verde, verás una "bola" negra con un contorno muy similar a la forma principal del conjunto.
- Dentro de esa "bola", hay otras más pequeñas que también se parecen a la original.
-
Recuadro violeta
-
Detalle del recuadro violeta
-
Detalle
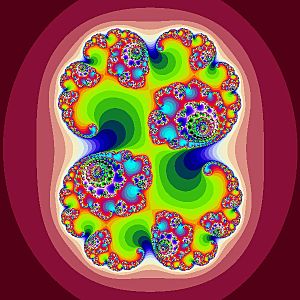
- Si amplías el recuadro gris o el recuadro violeta, notarás que las formas que aparecen son casi idénticas a la imagen inicial. Este proceso de encontrar formas similares puede repetirse infinitas veces.
Aunque a veces las figuras ampliadas pueden tener una ligera deformación, siguen siendo muy parecidas a la original. Es como si el conjunto tuviera "clones" de sí mismo por todas partes, sin importar cuánto lo amplíes.
- Otra forma de verlo
En algunas imágenes, el conjunto de Mandelbrot se ve igual, pero las líneas de colores que lo rodean pueden ser diferentes. Esto se debe a que se usó un criterio distinto para decidir cuándo un punto "escapa". Por ejemplo, en una imagen se puede considerar que escapa si se aleja más de 2 unidades, y en otra si se aleja más de 10. Esto cambia los colores, pero la forma negra del conjunto sigue siendo la misma.
El Conjunto de Mandelbrot y los Conjuntos de Julia
Existe otra forma de entender el conjunto de Mandelbrot: es el grupo de puntos c para los cuales el conjunto de Julia relacionado con la misma regla matemática (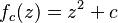
) es una figura "conectada" (es decir, no está hecha de pedacitos separados).
Imágenes Creadas con Ordenadores
Antes de que existieran los ordenadores digitales, era imposible ver la increíble complejidad del conjunto de Mandelbrot. Los ordenadores son esenciales para calcular y dibujar estas figuras.
En las siguientes imágenes, puedes ver cómo la calidad y el detalle del fractal mejoran a medida que se realizan más cálculos (iteraciones) por cada punto. Los puntos que pertenecen al conjunto de Mandelbrot (los que no "escapan") suelen aparecer en un color claro, como amarillo pálido. Los puntos que sí "escapan" se colorean con una escala de grises a negro, dependiendo de cuántos cálculos se necesitaron para que se hicieran grandes. Cuantos menos cálculos se necesiten para que un punto escape, más oscuro será su color.
-
10 iteraciones por píxel -
12 iteraciones por píxel -
15 iteraciones por píxel -
20 iteraciones por píxel -
50 iteraciones por píxel -
500 iteraciones por píxel
Más sobre el Conjunto de Mandelbrot
.jpg)
El conjunto de Mandelbrot es una figura "compacta" y "conectada", lo que significa que es una forma completa y sin agujeros. Su borde es muy especial: aunque es una línea, es tan intrincada que tiene una "dimensión" que la hace parecer más compleja de lo que esperarías.
Galería de imágenes
-
Recuadro verde
-
Minirecuadro gris
-
Recuadro blanco
-
Recuadro violeta
-
Detalle del recuadro violeta
-
Detalle
Véase también
En inglés: Mandelbrot set Facts for Kids
