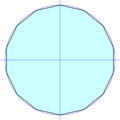
Polígono regular para niños
En geometría plana, un polígono regular es una figura cerrada con todos sus lados de la misma longitud y todos sus ángulos interiores iguales entre sí.
Los polígonos regulares más conocidos son el triángulo equilátero (con tres lados iguales) y el cuadrado (con cuatro lados iguales). Para figuras con más lados, simplemente añadimos la palabra "regular", como "pentágono regular" (cinco lados) o "hexágono regular" (seis lados).
Una característica interesante es que un polígono regular es siempre una figura convexa. Esto significa que si unes los puntos que dividen una circunferencia en partes iguales, obtendrás un polígono regular.
Contenido
Partes de un Polígono Regular
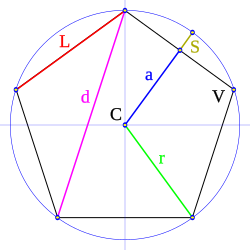
Los polígonos regulares tienen varias partes importantes:
- Lado (L): Es cada uno de los segmentos que forman el borde del polígono.
- Vértice (V): Es el punto donde se unen dos lados consecutivos.
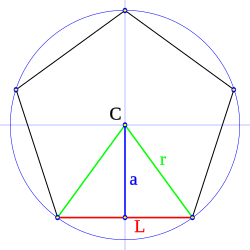
- Centro (C): Es el punto que está exactamente en el medio del polígono. Está a la misma distancia de todos los vértices y de todos los lados.
- Radio (r): Es el segmento que va desde el centro del polígono hasta uno de sus vértices.
- Apotema (a): Es un segmento que va desde el centro del polígono hasta el punto medio de uno de sus lados, formando un ángulo recto con ese lado.
- Diagonal (d): Es un segmento que une dos vértices que no están uno al lado del otro.
- Perímetro (P): Es la suma de las longitudes de todos sus lados. Es como el "contorno" del polígono.
- Semiperímetro (p): Es la mitad del perímetro.
Características Especiales de los Polígonos Regulares
- Todos los polígonos regulares son equiláteros, lo que significa que todos sus lados tienen la misma medida.
Ángulos en un Polígono Regular
Los polígonos regulares tienen diferentes tipos de ángulos:
Ángulo Central
El ángulo central de un polígono regular se forma en el centro del polígono, uniendo dos vértices consecutivos. Todos los ángulos centrales son iguales. Para calcularlo, divide 360 grados entre el número de lados (n) del polígono: 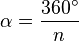
Ángulo Interior
El ángulo interior es el ángulo que se forma dentro del polígono, en cada vértice. Para calcularlo, usa esta fórmula: 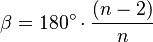 La suma de todos los ángulos interiores de un polígono regular se calcula así:
La suma de todos los ángulos interiores de un polígono regular se calcula así: 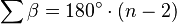
Ángulo Exterior
El ángulo exterior se forma al extender uno de los lados del polígono. Es el ángulo que está fuera de la figura, junto al ángulo interior. Para calcularlo, puedes restar el ángulo interior de 180 grados, o usar esta fórmula: 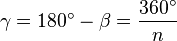 La suma de todos los ángulos exteriores de cualquier polígono (regular o no) siempre es 360 grados:
La suma de todos los ángulos exteriores de cualquier polígono (regular o no) siempre es 360 grados: 
Cómo Calcular el Área de un Polígono Regular
El área es la medida de la superficie que cubre el polígono. Hay varias maneras de calcularla.
Usando el Perímetro y la Apotema
Esta es una de las formas más comunes y sencillas. El área (A) de un polígono regular se calcula multiplicando su perímetro (P) por su apotema (a) y dividiendo el resultado entre 2: 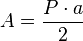 Esto funciona porque puedes imaginar que el polígono está formado por muchos triángulos iguales, donde la base de cada triángulo es un lado del polígono y la altura es la apotema.
Esto funciona porque puedes imaginar que el polígono está formado por muchos triángulos iguales, donde la base de cada triángulo es un lado del polígono y la altura es la apotema.
Usando el Número de Lados y la Apotema
Si conoces el número de lados (n) y la apotema (a), puedes usar esta fórmula: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A_p = a^2 \cdot n \cdot \tan \left ( \frac {\pi} {n} \right ) Aquí, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tan se refiere a la función tangente, que es parte de la Trigonometría.
Usando el Número de Lados y el Radio
Si conoces el número de lados (n) y el radio (r), puedes calcular el área así: 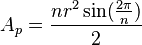 Aquí, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin se refiere a la función seno.
Aquí, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin se refiere a la función seno.
Diagonales
Número de Diagonales
Para saber cuántas diagonales tiene un polígono con "n" vértices (o lados), puedes usar esta fórmula: 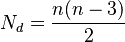 Por ejemplo, un cuadrado (n=4) tiene Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{4 (4-3)}{2} = \frac{4 \cdot 1}{2} = 2 diagonales.
Por ejemplo, un cuadrado (n=4) tiene Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{4 (4-3)}{2} = \frac{4 \cdot 1}{2} = 2 diagonales.
Longitud de la Diagonal Más Pequeña
La diagonal más corta de un polígono regular es la que une dos vértices que están separados por un solo vértice intermedio. Su longitud (d) se puede calcular con el radio (r) y el número de lados (n): 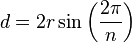
Galería de imágenes
Observación: Cuantos más lados tiene un polígono regular, más se parece a una circunferencia.
Véase también
 En inglés: Regular polygon Facts for Kids
En inglés: Regular polygon Facts for Kids
- Figuras geométricas
- Polígono
- Polígono equilátero
- Estrella (figura geométrica)
- Regla y compás
- Trigonometría