Resorte para niños
Un resorte (también llamado muelle) es un objeto especial que puede guardar energía y luego liberarla sin romperse ni cambiar su forma de manera permanente. Imagina que lo estiras o lo aprietas, y cuando lo sueltas, vuelve a su tamaño original. Esto es posible porque están hechos de materiales elásticos, como diferentes tipos de acero, bronce o incluso plástico.
Los resortes se usan en muchísimos objetos de nuestro día a día, desde herramientas y máquinas hasta las suspensiones de los coches. Su principal función es resistir o amortiguar las fuerzas que se les aplican, devolviendo esa energía.
Contenido
¿Cómo surgieron los resortes?
Desde hace muchísimo tiempo, la gente ha usado materiales elásticos. Por ejemplo, los arcos de madera para lanzar flechas se usaban hace más de 60.000 años. En la Edad del Bronce, ya existían resortes más complejos. Se usaban en objetos sencillos como las fíbulas (broches para sujetar la ropa) o las pinzas.
Un inventor llamado Ctesibio de Alejandría, hace mucho tiempo, incluso fabricó aleaciones de bronce especiales para hacer resortes más elásticos.
Los resortes hechos con tiras de metal enrolladas se empezaron a usar en los relojes a principios del siglo XV. Gracias a ellos, los relojes podían funcionar sin parar. En 1673, se inventó el resorte espiral para los relojes de bolsillo, lo que los hizo más precisos.
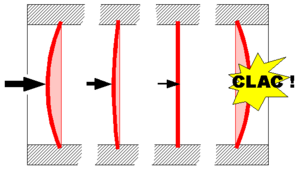
En 1676, un científico británico llamado Robert Hooke descubrió una ley muy importante sobre los resortes. Su Ley de la elasticidad dice que la deformación de un resorte (cuánto se estira o se encoge) es directamente proporcional a la fuerza que se le aplica. Es decir, si aplicas el doble de fuerza, se estira el doble.
Con la llegada del ferrocarril en el siglo XIX, y gracias a los avances en la fabricación de metales y máquinas, los resortes dejaron de ser algo que los artesanos hacían a mano. Empezaron a producirse en grandes cantidades en fábricas. Así, los resortes se convirtieron en una parte esencial de casi todas las máquinas y objetos que se fabricaban en masa, como relojes, máquinas de coser, coches, colchones y electrodomésticos. Hoy en día, los resortes están por todas partes, desde un simple imperdible hasta la suspensión de un tren.
¿Qué tipos de resortes existen?
Los resortes se pueden clasificar de muchas maneras, según su forma, cómo se les aplica la fuerza, cómo responden o para qué se usan.
Según su forma
- Muelles planos: Son láminas de metal planas. Un ejemplo son las ballestas que se usan en las suspensiones de muchos vehículos grandes.
- Muelles espirales: Son una cinta larga de metal enrollada sobre sí misma. Se usan en los relojes mecánicos "de cuerda".
- Muelles helicoidales: Son los más comunes. Parecen un alambre enrollado en forma de espiral alrededor de un cilindro. Funcionan cambiando la distancia entre sus vueltas.
- Barras de torsión: Son piezas largas y flexibles que se retuercen cuando se les aplica una fuerza de giro. Se usan en las suspensiones de algunos vehículos.
- Clips: Son piezas con formas muy variadas que no encajan en las categorías anteriores, pero que también usan la elasticidad. Un ejemplo son los clips que sujetan los rieles del tren.
Según cómo se les aplica la fuerza
- Resorte de flexión: La fuerza se aplica de lado, haciendo que el resorte se doble. Al quitar la fuerza, vuelve a su forma. Las ballestas son un ejemplo.
- Resorte de tracción: Están hechos para estirarse cuando se les aplica una fuerza. Tienen ganchos en los extremos para poder sujetarlos.
- Resorte de compresión: Están hechos para acortarse cuando se les aplica una fuerza. Pueden tener diferentes formas, como cilíndricas o cónicas.
- Resorte de torsión: La fuerza que se les aplica es un giro, y el resorte gira a medida que se le aplica la carga.
Según cómo responden a la carga
- Muelle constante: Ofrece la misma resistencia sin importar cuánto se deforme.
- Muelle variable: Su resistencia cambia a medida que se comprime.
- Muelle de rigidez ajustable: Su resistencia se puede cambiar con un sistema de control.
- Muelle de pandeo: Un tipo especial que se usa en los teclados de ordenador. Cuando se presiona lo suficiente, el muelle se "colapsa" de repente, enviando una señal.
Según su fabricación
- Muelle plano: Hecho de láminas de acero elástico.
- Muelle bobinado: Un alambre o barra de metal enrollado.
- Muelle mecanizado: Hecho trabajando barras de acero con máquinas, no enrollando.
- Muelle de serpentina: Un alambre grueso en forma de zig-zag, usado en muebles.
- Muelle anular: Un resorte helicoidal de acero con sus extremos unidos formando un anillo.
Tipos más utilizados
- Muelle en voladizo: Un resorte fijado solo por un extremo, como las tablas de salto en una piscina.
- Muelle helicoidal: El más común, con tres tipos principales:
* Resortes de extensión: Se alargan al cargarse. Sus espiras suelen tocarse cuando no están cargados. * Resortes de compresión: Se acortan al cargarse. Sus espiras no se tocan cuando no están cargados. * Resortes de tubos huecos: Pueden ser de extensión o compresión. Se llenan de aceite y su rigidez se puede ajustar.
- Resorte de voluta: Un resorte helicoidal con forma de cono, que permite un recorrido más largo al comprimirse.
- Resorte regulador: Un resorte espiral muy delicado usado en relojes y otros mecanismos de precisión.
- Suspensión de ballesta: Un resorte plano usado en las suspensiones de vehículos y en arcos.
- Muelle en V: Usado en mecanismos de armas antiguas y en pestillos de puertas.
Otros tipos
- Muelle Belleville: Un resorte en forma de disco que se usa para aplicar tensión a un tornillo.
- Muelle de fuerza constante: Una cinta elástica enrollada que ejerce una fuerza casi igual a medida que se desenrolla.
- Muelle de gas: Un volumen de gas comprimido que actúa como resorte.
- Resorte motor: Un resorte en forma de cinta espiral que da energía a mecanismos de relojería, cajas de música o juguetes de cuerda.
- Muelle con retención: Una banda de metal que, al desenrollarse, produce una fuerza constante. Se usa en las cintas métricas.
- Muelles helicoidales de velocidad progresiva: Su resistencia cambia a medida que se comprimen, porque algunas espiras se tocan antes que otras.
- Goma elástica: Almacena energía al estirarse.
- Arandela elástica: Se usa para aplicar una fuerza constante a un tornillo.
- Resorte de torsión: Cualquier resorte diseñado para ser torcido, no comprimido o estirado.
- Muelle ondulado: Resortes, arandelas o expansores con forma ondulada.
Modelo teórico: Muelle ideal
En física, a veces se usa un "muelle ideal" para simplificar los cálculos. Este muelle no tiene peso ni masa, y su fuerza es exactamente proporcional a cuánto se estira o comprime.
¿Para qué se usan los resortes?
Los resortes tienen muchísimos usos en nuestra vida diaria:
- Vehículos: En las suspensiones de coches y camiones.
- Relojes: Para hacer funcionar los mecanismos internos y para sujetar las correas.
- Imperdibles
- Joyería: En los cierres de collares y pulseras.
- Mecanismos de cierre: Para que las llaves funcionen y las cerraduras se cierren bien.
- Bandejas mecánicas: En lectores de CD o magnetófonos.
- Bolígrafos
- Colchones de muelles
- Slinky: Un famoso juguete con forma de muelle.
- Cama elástica
- Pogo saltarín
- Teclados con muelles de pandeo
- Muelles de tapicería en sofás y sillas.
- Juguetes
- Armas de aire comprimido
- Armas de fuego
- Jarcias de amarre de una embarcación.
La física de los resortes
En la física, un resorte se ve como un objeto que guarda energía potencial. Esta energía se almacena al estirar o comprimir los enlaces entre los átomos del material elástico.
La ley de Hooke es fundamental para entender cómo funcionan los resortes. Dice que la fuerza que aplicas a un resorte es directamente proporcional a cuánto se estira o se encoge. Esto solo es cierto si la deformación es pequeña. Si estiras o comprimes demasiado un resorte, puede romperse o deformarse para siempre.
La energía que un resorte almacena cuando se estira o se comprime se puede calcular con una fórmula sencilla: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): U_k = \frac{1}{2} kx^2 Donde:
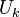 es la energía almacenada.
es la energía almacenada.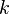 es la constante elástica del resorte (un número que indica lo "duro" que es el resorte).
es la constante elástica del resorte (un número que indica lo "duro" que es el resorte). es cuánto se ha estirado o comprimido el resorte desde su posición de reposo.
es cuánto se ha estirado o comprimido el resorte desde su posición de reposo.
Resortes de longitud cero
Un "resorte de longitud cero" es un tipo especial de resorte helicoidal que, si pudiera encogerse por completo, no ejercería ninguna fuerza. En la práctica, se fabrican con una tensión interna para que su punto de equilibrio (donde no ejercen fuerza) esté en una longitud "negativa". Al combinarlos con un trozo de material que no se estira, se logra que el punto de fuerza cero esté en la longitud cero.
Estos resortes se usan en instrumentos muy sensibles como los sismógrafos, que detectan terremotos, o los gravímetros, que miden pequeños cambios en la gravedad. También se usan en los cierres de puertas para que la puerta se mantenga bien cerrada.
Véase también
 En inglés: Spring (device) Facts for Kids
En inglés: Spring (device) Facts for Kids