Poliedro regular para Niños

**Poliedros regulares**
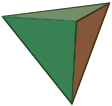
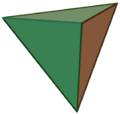
Tetraedro
	Dual: Tetraedro
	Símbolo de Schläfli: 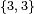$\scriptstyle \{3, \, 3\}$
	Símbolo de Wythoff: 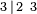$\scriptstyle 3\,\|\,2 \ 3$
	Familia: Sólidos de Platón
	Poliedro convexo
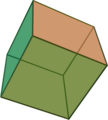
Hexaedro, Cubo
	Dual: Octaedro
	Símbolo de Schläfli: 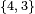$\scriptstyle \{4, \, 3\}$
	Símbolo de Wythoff: 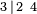$\scriptstyle 3\,\|\,2 \ 4$
	Familia: Sólidos de Platón
	Poliedro convexo
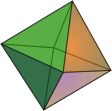
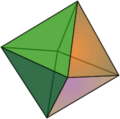
Octaedro
	Dual: Cubo
	Símbolo de Schläfli: 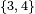$\scriptstyle \{3, \, 4\}$
	Símbolo de Wythoff: 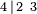$\scriptstyle 4\,\|\,2 \ 3$
	Familia: Sólidos de Platón
	Poliedro convexo
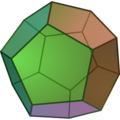
Dodecaedro
	Dual: Icosaedro
	Símbolo de Schläfli: 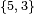$\scriptstyle \{5, \, 3\}$
	Símbolo de Wythoff: 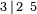$\scriptstyle 3\,\|\,2 \ 5$
	Familia: Sólidos de Platón
	Poliedro convexo
Icosaedro
	Dual: Dodecaedro
	Símbolo de Schläfli: 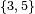$\scriptstyle \{3, \, 5\}$
	Símbolo de Wythoff: 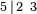$\scriptstyle 5\,\|\,2 \ 3$
	Familia: Sólidos de Platón
	Poliedro convexo
Pequeño dodecaedro estrellado
	Dual: Pequeño dodecaedro estrellado
	Símbolo de Schläfli: 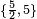$\scriptstyle \{ {5 \over 2}, \, 5\}$
	Símbolo de Wythoff: 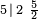$\scriptstyle 5\,\|\,2 \ {5 \over 2}$
	Familia: Sólidos de Kepler-Poinsot
	Poliedro no convexo
Gran dodecaedro estrellado
	Dual: Gran dodecaedro estrellado
	Símbolo de Schläfli: 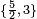$\scriptstyle \{ {5 \over 2}, \, 3\}$
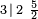	Símbolo de Wythoff: $\scriptstyle 3\,\|\,2 \ {5 \over 2}$
	Familia: Sólidos de Kepler-Poinsot
	Poliedro no convexo
Gran dodecaedro
	Dual: Gran dodecaedro
	Símbolo de Schläfli: 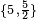$\scriptstyle \{ 5\, , {5 \over 2} \}$
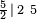	Símbolo de Wythoff: $\scriptstyle {5 \over 2}\,\|\,2 \ 5$
	Familia: Sólidos de Kepler-Poinsot
	Poliedro no convexo
Gran icosaedro
	Dual: Gran icosaedro
	Símbolo de Schläfli: 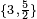$\scriptstyle \{ 3\, , {5 \over 2} \}$
	Símbolo de Wythoff: 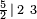$\scriptstyle {5 \over 2}\,\|\,2 \ 3$
	Familia: Sólidos de Kepler-Poinsot
	Poliedro no convexo

Un poliedro regular es una figura geométrica tridimensional. Sus caras son todas polígonos regulares idénticos. Además, todos sus ángulos y esquinas son iguales. Puedes identificar un poliedro regular por su símbolo de Schläfli, que se escribe como {n, m}. Aquí, "n" es el número de lados de cada cara, y "m" es cuántas caras se unen en cada vértice (esquina).

Contenido

¿Qué son los Poliedros Regulares?
- La Historia de los Poliedros Regulares
  - ¿Por qué algunos poliedros son "más regulares" que otros?
  - El Descubrimiento de los Poliedros No Convexos
¿Para qué se usan los Poliedros Regulares?
Galería de imágenes
Véase también

¿Qué son los Poliedros Regulares?

Se conocen nueve tipos de poliedros regulares. Estos se dividen en dos grupos principales. Cinco de ellos son poliedros convexos, que son los famosos sólidos de Platón. Los otros cuatro son poliedros no convexos, conocidos como los sólidos de Kepler-Poinsot.

La Historia de los Poliedros Regulares

Los cinco poliedros regulares convexos fueron estudiados por el filósofo griego Platón. Él se asombró con sus formas perfectas. Platón asoció cada uno de estos sólidos con un "elemento" fundamental de la naturaleza: aire, agua, tierra y fuego. El dodecaedro lo relacionó con un "quinto elemento" o espíritu.

Muchos científicos creen que esta idea de Platón fue un paso importante. Ayudó a entender cómo se forman las moléculas. Esto se debe a que muchos cristales tienen una estructura atómica que se parece a estos poliedros.

¿Por qué algunos poliedros son "más regulares" que otros?

Para algunos expertos, solo los sólidos de Platón son "verdaderamente" regulares. Esto es porque los otros cuatro poliedros (los de Kepler-Poinsot) tienen caras que se cruzan entre sí. Por eso, es difícil construirlos en la vida real de forma perfecta. Las representaciones que vemos son solo modelos.

El Descubrimiento de los Poliedros No Convexos

Los cuatro poliedros regulares no convexos no fueron conocidos por los matemáticos antiguos. Fueron descubiertos mucho después:

El pequeño dodecaedro estrellado apareció en un mosaico en Venecia, Italia, alrededor del año 1430. Lo hizo el artista Paolo Uccello.
El gran dodecaedro estrellado fue mostrado por Wenzel Jamnitzer en 1568.
El astrónomo Johannes Kepler redescubrió estos dos poliedros en 1619. Los describió en su libro Harmonices mundi.
Los otros dos sólidos, el gran dodecaedro y el gran icosaedro, fueron descubiertos más tarde por Louis Poinsot en 1809.

¿Para qué se usan los Poliedros Regulares?

Los poliedros regulares y sus combinaciones se usan en muchos campos. Aunque al combinarlos se pierde un poco de su uniformidad, mantienen sus propiedades especiales.

Aplicaciones en Diseño y Construcción

Muchos poliedros arquimedianos (que son parientes de los regulares) tienen ángulos iguales. Esto los hace útiles para crear estructuras que se "empaquetan" bien.
La forma poliédrica es muy estable. Permite construir edificios altos y fuertes. Incluso se pueden usar materiales ligeros como el bambú.
Se usan en el diseño industrial y la arquitectura. Por ejemplo, para crear habitaciones, estructuras espaciales planas y cúpulas geodésicas. También se usaron en el pasado para construir cúpulas de piedra.

Poliedros en la Naturaleza y la Ingeniería

Las formas poliédricas también se encuentran en la naturaleza. Por ejemplo, en la estructura de algunos minerales y en partes de seres vivos.
El tetraedro regular es la base para construir rompeolas especiales. Estas estructuras, como el tetrápodo y el Dolos, se usan en las costas para protegerlas de las olas.
La combinación de tetraedros se ha usado en proyectos de viviendas prefabricadas. Esto permite construir casas rápidamente.

Las Cúpulas Geodésicas: Un Ejemplo Famoso

Las estructuras basadas en poliedros, como la cúpula geodésica, son muy importantes en arquitectura. Permiten construir techos muy ligeros que cubren grandes espacios. Su desarrollo se debe a las investigaciones de Buckminster Fuller en los años 1950. Él se inspiró en las estructuras de los Radiolarios, unos pequeños organismos marinos.

Estas estructuras, como las cúpulas geodésicas, son ligeras y se pueden adaptar a diferentes necesidades. Están hechas de nudos y barras, y a menudo se pueden desmontar y reutilizar. Tienen muchas aplicaciones en la arquitectura, tanto para construcciones temporales como permanentes.

Galería de imágenes

Un tetraedro, el poliedro regular más simple.
Un hexaedro o cubo, una forma muy común.
Un octaedro, que tiene ocho caras triangulares.
Un dodecaedro, con doce caras pentagonales.
Un icosaedro, con veinte caras triangulares.
El pequeño dodecaedro estrellado, un poliedro no convexo.
El gran dodecaedro estrellado, otra forma no convexa.
El gran dodecaedro, con caras que se cruzan.
El gran icosaedro, un poliedro no convexo complejo.

Véase también

En inglés: Regular polytope Facts for Kids

Poliedro
Poliedro semirregular
Polígono regular
Politopo regular
Sólido de Kepler-Poinsot
Sólido platónico
Teselado regular

Obtenido de «https://ninos.kiddle.co/index.php?title=Poliedro_regular&oldid=5007470»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Poliedro regular para Niños. Enciclopedia Kiddle.

Poliedro regular para niños