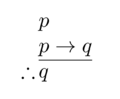Lógica para niños
La lógica es como un detective del pensamiento. Es una parte de la filosofía y las matemáticas que nos ayuda a entender cómo razonamos, cómo construimos argumentos válidos y cómo evitamos caer en errores. Imagina que es el estudio de las reglas que hacen que nuestras ideas y conclusiones sean sólidas y tengan sentido.
La lógica nos enseña a pensar de forma clara y ordenada. Nos ayuda a distinguir entre lo que es una buena razón para creer algo y lo que no lo es. También nos muestra cómo identificar las falacias, que son argumentos que parecen correctos pero no lo son, y las paradojas, que son ideas que parecen contradecirse a sí mismas.
Existen diferentes tipos de lógica, cada una enfocada en un área específica:
- La lógica filosófica explora cómo usamos el lenguaje y las ideas para argumentar.
- La lógica matemática usa símbolos y reglas muy precisas para analizar el razonamiento, como si fuera un lenguaje de códigos.
- La lógica informal se centra en cómo razonamos en nuestra vida diaria y cómo podemos mejorar nuestros argumentos al hablar o escribir.
- La lógica computacional aplica las ideas de la lógica matemática para crear programas de computadora y entender cómo funcionan las máquinas.
La lógica ha existido desde hace mucho tiempo, con orígenes en lugares como China, India y Grecia. Al principio, se consideraba principalmente una parte de la filosofía. Pero en el siglo XX, con el desarrollo de la lógica matemática, también se convirtió en una parte importante de las matemáticas y de la ciencia de la computación.
Aunque no todos están de acuerdo en una única definición de lógica, en general, su estudio incluye:
- Clasificar los argumentos.
- Analizar las formas en que se construyen las ideas.
- Estudiar si las conclusiones se derivan correctamente de las ideas iniciales.
- Entender los argumentos que tienen errores, como las falacias.
- Investigar las paradojas.
- Estudiar cómo funcionan los lenguajes formales (como los de las matemáticas o la programación).
- Explorar los conceptos de significado y verdad.
La lógica es un campo de estudio que conecta muchas áreas del conocimiento, como la filosofía, las matemáticas, la informática, la lingüística y las ciencias cognitivas.
Contenido
- ¿De dónde viene la palabra "lógica"?
- Conceptos clave de la lógica
- Tipos de lógica
- Lógica matemática: el lenguaje de los símbolos
- Lógica computacional: la lógica de las computadoras
- Lógica filosófica: el estudio del razonamiento en la filosofía
- Lógica informal: el arte de argumentar en la vida diaria
- Lógica silogística: los inicios del razonamiento formal
- Lógica proposicional: combinando afirmaciones
- Lógica modal: más allá de lo verdadero y falso
- Lógica de predicados: analizando detalles
- Lógica no clásica: desafiando las reglas
- Historia de la lógica
- Galería de imágenes
- Véase también
¿De dónde viene la palabra "lógica"?
La palabra "lógica" viene del griego antiguo logikḗ, que significa "dotada de razón" o "argumentativa". A su vez, esta palabra viene de lógos, que puede significar "palabra", "pensamiento", "idea", "argumento" o "razón".
En nuestro día a día, cuando decimos que algo tiene "lógica" o que alguien tiene un "pensamiento lógico", nos referimos a que sus ideas son coherentes, razonables y claras. Por ejemplo, si un plan para organizar un evento tiene "lógica", significa que está bien pensado y es probable que funcione. Esto es lo que llamamos "lógica cotidiana" o "lógica del sentido común".
Lógica cotidiana vs. lógica formal
La "lógica cotidiana" se basa en nuestra experiencia y en lo que nos parece razonable en situaciones normales. Por ejemplo, la "lógica deportiva" se refiere a las reglas no escritas o las expectativas que tenemos en un deporte.
En cambio, la lógica formal es mucho más estricta. Se enfoca en reglas precisas que determinan si un argumento es válido, sin importar si lo que dice es verdad o no. Es como un juego con reglas muy claras: si sigues las reglas, tu movimiento es válido, incluso si el resultado final es inesperado. Esta lógica es fundamental en las matemáticas y la informática.
Conceptos clave de la lógica
¿Qué es una inferencia?
La inferencia es el proceso por el cual se derivan conclusiones a partir de premisas o hipótesis iniciales. Cuando una conclusión se sigue de sus premisas o hipótesis de partida, por medio de deducciones lógicas válidas, se dice que las premisas implican (infieren) la conclusión.
La inferencia es el objeto de estudio tradicional de la lógica, así como la vida es el objeto de estudio de la biología. La lógica investiga los fundamentos por los cuales algunas inferencias son aceptables, y otras no. Cuando una inferencia es aceptable, lo es por su estructura lógica y no por el contenido específico del argumento o el lenguaje utilizado (retórica). Por esto se construyen sistemas lógicos que capturan los factores relevantes de las deducciones que aparecen en el lenguaje natural.
Tradicionalmente, se distinguen tres clases de inferencias: las deducciones, las inducciones y las abducciones, aunque a veces se cuenta a la abducción como un caso especial de inducción. Las inducciones se estudian desde la lógica inductiva y el problema de la inducción. Las deducciones, en cambio, son estudiadas por la mayor parte de la lógica contemporánea.
En las investigaciones sobre la inteligencia artificial, la inferencia es la operación lógica utilizada en los motores de inferencia de los sistemas expertos.
Una inferencia es el acto de sacar una conclusión a partir de información que ya tenemos. Es como cuando ves huellas en el suelo y "infieres" que alguien pasó por ahí. La lógica estudia qué inferencias son correctas y cuáles no.
Hay diferentes tipos de inferencias:
- Deducción: Si las ideas iniciales son verdaderas, la conclusión *debe* ser verdadera. Por ejemplo, "Todos los perros ladran. Max es un perro. Por lo tanto, Max ladra."
- Inducción: La conclusión es probable, pero no segura. Por ejemplo, "Cada vez que he visto un cuervo, era negro. Por lo tanto, todos los cuervos son negros." (Podría haber uno blanco que no hemos visto).
¿Qué significa que un argumento sea válido?
En lógica, la validez es una propiedad que tienen los argumentos cuando las premisas implican la conclusión. Si la conclusión es una consecuencia lógica de las premisas, se dice que el argumento es deductivamente válido. Algunos consideran estas dos nociones idénticas y usan ambos términos indistintamente. Otros, sin embargo, consideran que puede haber argumentos que no sean deductivamente válidos, como las inducciones. En cualquier caso, de las inducciones a veces se dice que son buenas o malas, en vez de válidas o inválidas.
Ejemplos de argumentos deductivamente válidos son los siguientes:
|
|
|
Para que un argumento sea lo que le da principalmente la validez a un argumento es la seguridad con lo que lo dice la persona y que tenga razón con lo que dice deductivamente válido, no es necesario que las premisas o la conclusión sean verdaderas. Sólo se requiere que la conclusión sea una consecuencia lógica de las premisas. La lógica formal exige únicamente una relación condicional entre las premisas y la conclusión. Esto es: que si las premisas son verdaderas, entonces la conclusión también lo es (esta es la caracterización semántica de la noción de consecuencia lógica); o alternativamente: que la conclusión sea deducible de las premisas conforme a las reglas de un sistema lógico (esta es la caracterización sintáctica de la noción de consecuencia lógica). Si un argumento, además de ser válido, tiene premisas verdaderas, entonces se dice que es sólido.
Las expresiones de las que depende la validez de los argumentos se llaman constantes lógicas, y la lógica las estudia mediante sistemas formales.
En lógica, la validez se refiere a la estructura de un argumento. Un argumento es válido si su conclusión *tiene que ser* verdadera si sus ideas iniciales (premisas) son verdaderas. No importa si las premisas son realmente ciertas o no, solo importa la conexión lógica entre ellas y la conclusión.
Por ejemplo:
- Si todos los gatos vuelan y mi mascota es un gato, entonces mi mascota vuela. (Este argumento es válido, aunque los gatos no vuelen en la realidad).
Si un argumento es válido y, además, sus premisas son verdaderas, entonces se dice que es un argumento sólido.
¿Qué son las falacias?
En lógica, una falacia (del latín fallacia ‘engaño’) es una tesis que parece válida, pero no lo es. Algunas falacias se cometen intencionadamente para persuadir o manipular a los demás, mientras que otras se cometen sin intención debido a descuidos o ignorancia. En ocasiones las falacias pueden ser muy sutiles y persuasivas, por lo que se debe poner mucha atención para detectarlas.
Que un argumento sea falaz no implica que sus premisas o su conclusión sean falsas ni que sean verdaderas. Un argumento puede tener premisas y conclusión verdaderas y aun así ser falaz. Lo que hace falaz a un argumento es la invalidez del argumento en sí. De hecho, inferir que una proposición es falsa porque el argumento que la contiene por conclusión es falaz es en sí una falacia conocida como argumento ad logicam.
El estudio de las falacias se remonta por lo menos hasta Aristóteles, quien en sus Refutaciones sofísticas identificó y clasificó trece clases de falacias. Desde entonces se han agregado a la lista cientos de otras falacias y se han propuesto varios sistemas de clasificación.
Las falacias son de interés no solo para la lógica, sino también para la política, la retórica, el derecho, la ciencia, la religión, el periodismo, la mercadotecnia, el cine y, en general, cualquier área en la cual la argumentación y la persuasión sean de especial relevancia.
Una falacia es un argumento que parece correcto y convincente, pero en realidad tiene un error lógico. Es como un truco mental que nos puede engañar. A veces, las personas usan falacias a propósito para convencer a otros, pero muchas veces se cometen sin querer, por un descuido o por no saber de lógica.
Por ejemplo, una falacia común es decir: "Si mucha gente cree algo, entonces debe ser verdad". Esto no es necesariamente cierto, ya que muchas personas pueden estar equivocadas.
¿Qué son las paradojas?

Una paradoja (del latín paradoxa, ‘lo contrario a la opinión común’) o antilogía es una idea lógicamente contradictoria u opuesta a lo que se considera verdadero a la opinión general. También se considera paradoja a una proposición en apariencia falsa o que infringe el sentido común, pero no conlleva una contradicción lógica, en contraposición a un sofisma, que solo aparenta ser un razonamiento válido. Algunas paradojas son razonamientos en apariencia válidos, que parten de premisas en apariencia verdaderas, pero que conducen a contradicciones o situaciones contrarias al sentido común. En la retórica, es una figura de pensamiento que consiste en emplear expresiones o frases que implican contradicción. Las paradojas son estímulo para la reflexión y a menudo los filósofos se sirven de ellas para revelar la complejidad de la realidad. La paradoja también permite demostrar las limitaciones de la comprensión humana; la identificación de paradojas basadas en conceptos que a simple vista parecen sencillos y razonables ha impulsado importantes avances en la ciencia, la filosofía y las matemáticas.
Una paradoja es una afirmación o situación que parece contradecirse a sí misma o va en contra de lo que normalmente pensamos. A veces, las paradojas nos hacen pensar profundamente y han ayudado a la ciencia y la filosofía a descubrir cosas nuevas.
Un ejemplo famoso es la paradoja del mentiroso: "Esta frase es falsa". Si la frase es verdadera, entonces es falsa, lo cual es una contradicción. Si es falsa, entonces es verdadera, lo cual también es una contradicción.
¿Qué es la verdad en lógica?
La verdad es la coincidencia entre una afirmación y los hechos, o la realidad a la que dicha afirmación se refiere. Otra teoría es la que considera la verdad como descubrimiento o iluminación que el hombre hace de la realidad: «fue Ortega, en 1914, quien hizo el primer uso filosófico de la palabra griega alétheia con el significado de descubrimiento o iluminación: se trata de una innovación significativa porque Ortega introdujo una acepción nueva, sirviéndose de esa palabra, para superar la idea, que le parecía inaceptable, de que la verdad tenga que ser adecuación. Después de Ortega, los demás filósofos, a partir de 1927 con Heidegger, no saben de dónde procede la interpretación etimológica que ellos dan como obvia para sus reflexiones filosóficas sobre la verdad».
El término se usa tanto en un uso vulgar de la lengua como en un sentido técnico en diversos campos como la filosofía, la lógica, las matemáticas y la ciencia.
El uso de la palabra verdad abarca asimismo la honestidad, la buena fe y la sinceridad humana en general; también el acuerdo de los conocimientos con las cosas que se afirman como realidades: los hechos o la cosa en particular; y, finalmente, la relación de los hechos o las cosas en su totalidad en la constitución del Todo, el Universo.
Las cosas son verdaderas cuando son «fiables», cuando cumplen lo que ofrecen.
El término no tiene una única definición en la que estén de acuerdo la mayoría de los estudiosos y las teorías sobre la verdad continúan siendo ampliamente debatidas. Hay posiciones diferentes acerca de cuestiones como:
- Qué es lo que constituye la verdad.
- Con qué criterio podemos identificarla y definirla.
- Si el ser humano posee conocimientos innatos o solo puede adquirirlos.
- Si existen las revelaciones o la verdad puede alcanzarse tan solo mediante la experiencia, el entendimiento y la razón.
- Si la verdad es subjetiva u objetiva.
- Si la verdad es relativa o absoluta.
- Y hasta qué grado pueden afirmarse cada una de dichas propiedades.
Este artículo procura introducir las principales interpretaciones y perspectivas, tanto históricas como actuales, acerca de este concepto.
La pregunta por la verdad es y ha sido objeto de debate entre teólogos, filósofos y lógicos a lo largo de los siglos considerándose un tema concerniente al alma y al estudio de una llamada psicología racional dentro del campo de la filosofía.
En la actualidad es un tema de investigación científica así como de fundamentación filosófica:
- La investigación científica de la función cognitiva introduce nuevas perspectivas acerca del conocimiento basado en la evidencia como creencia epistemológicamente verdadera con justificación válida.
- Interesa a la lingüística pues el lenguaje es expresión de la propia verdad.
- Interesa a la antropología filosófica, pues parece evidente que los seres humanos prefieren la verdad a la falsedad, al error o la mentira y prefieren la certeza a la duda.
- Interesa a la historia, por cuanto el aprecio hacia la verdad y la condena de la mentira o del error varía en intensidad según las épocas y las culturas, pues tanto el concepto de verdad como su valoración no siempre es el mismo a lo largo de la historia y según las diferentes culturas.
- Interesa a la ciencia en cuanto tal en su pretensión de conocimiento válido.
En lógica, la verdad se refiere a si una afirmación coincide con los hechos o la realidad. Si digo "El cielo es azul" y realmente es azul, entonces la afirmación es verdadera.
La idea de "verdad" es muy importante y ha sido estudiada por filósofos y científicos durante siglos. Hay muchas preguntas sobre la verdad: ¿Cómo sabemos si algo es verdad? ¿La verdad es la misma para todos o cambia según la persona? La lógica nos ayuda a explorar estas preguntas de manera estructurada.
Tipos de lógica
Lógica matemática: el lenguaje de los símbolos
La lógica matemática, también llamada lógica simbólica, lógica teorética, lógica formal o logística, es el estudio formal y simbólico de la lógica, y su aplicación a algunas áreas de la matemática y la ciencia. Comprende la aplicación de las técnicas de la lógica formal a la construcción y el desarrollo de las matemáticas y el razonamiento matemático, y conversamente la aplicación de técnicas matemáticas a la representación y el análisis de la lógica formal. La investigación en lógica matemática ha jugado un papel crucial en el estudio de los fundamentos de las matemáticas.
La lógica matemática estudia la inferencia mediante la construcción de sistemas formales como la lógica proposicional, la lógica de primer orden o la lógica modal. Estos sistemas capturan las características esenciales de las inferencias válidas en los lenguajes naturales, pero al ser estructuras formales susceptibles de análisis matemático, permiten realizar demostraciones rigurosas sobre ellas.
La lógica matemática se suele dividir en cuatro áreas: teoría de modelos, teoría de la demostración, teoría de conjuntos y teoría de la computabilidad. La teoría de la demostración y la teoría de modelos fueron el fundamento de la lógica matemática. La teoría de conjuntos se originó en el estudio del infinito por Georg Cantor y ha sido la fuente de muchos de los temas más desafiantes e importantes de la lógica matemática, desde el teorema de Cantor, el axioma de elección y la cuestión de la independencia de la hipótesis del continuo, al debate moderno sobre grandes axiomas cardinales. La lógica matemática tiene estrechas conexiones con las ciencias de la computación. La teoría de la computabilidad captura la idea de la computación en términos lógicos y aritméticos. Sus logros más clásicos son la indecidibilidad del Entscheidungsproblem de Alan Turing y su presentación de la tesis de Church-Turing. Hoy en día, la teoría de la computabilidad se ocupa principalmente del problema más refinado de las clases de complejidad (¿cuándo es un problema eficientemente solucionable?) y de la clasificación de los grados de insolubilidad.
La lógica matemática también estudia las definiciones de nociones y objetos matemáticos básicos como conjuntos, números, demostraciones y algoritmos. La lógica matemática estudia las reglas de deducción formales, las capacidades expresivas de los diferentes lenguajes formales y las propiedades metalógicas de los mismos.
En un nivel elemental, la lógica proporciona reglas y técnicas para determinar si es o no válido un argumento dado dentro de un determinado sistema formal. En un nivel avanzado, la lógica matemática se ocupa de la posibilidad de axiomatizar las teorías matemáticas, de clasificar su capacidad expresiva, y desarrollar métodos computacionales útiles en sistemas formales. La teoría de la demostración y la matemática inversa son dos de los razonamientos más recientes de la lógica matemática abstracta. Debe señalarse que la lógica matemática se ocupa de sistemas formalizados que pueden no ser equivalentes en todos sus aspectos, por lo que la lógica matemática no es un método para descubrir verdades del mundo físico real, sino solo una fuente posible de modelos lógicos aplicables a teorías científicas, muy especialmente a la matemática convencional.
Por otra parte, la lógica matemática no estudia el concepto de razonamiento humano general o el proceso creativo de construcción de demostraciones matemáticas mediante argumentos rigurosos pero con lenguaje informal con algunos signos o diagramas, sino solo de demostraciones y razonamientos que se pueden formalizar por completo.
La lógica matemática usa símbolos y reglas muy precisas para analizar el razonamiento. Es como un lenguaje especial que permite a los matemáticos y científicos construir pruebas muy rigurosas. Se usa para entender cómo funcionan los números, los conjuntos y los algoritmos.
Esta rama de la lógica es clave para los fundamentos de las matemáticas y tiene una conexión muy fuerte con la informática.
Lógica computacional: la lógica de las computadoras
La lógica computacional es la misma lógica matemática aplicada al contexto de las ciencias de la computación. Su uso es fundamental en varios niveles: en los circuitos computacionales, en la programación lógica y en el análisis y optimización (de recursos temporales y espaciales) de algoritmos.
La lógica se extiende al corazón de la informática a medida que surge como una disciplina: El trabajo de Alan Turing sobre el Entscheidungsproblem seguido del trabajo de Kurt Gödel sobre teoremas incompletos. La noción de la computadora de uso general que surgió de este trabajo fue de gran importancia para los diseñadores de la maquinaria informática en la década de 1940.
En los años 50 y 60, investigaciones predijeron que, cuando el conocimiento humano se pudiera expresar usando la lógica con notaciones matemáticas, sería posible crear una máquina capaz de razonar o una inteligencia artificial. Esto fue más difícil de lo esperado a causa de la complejidad del razonamiento humano. En la lógica de programación, un programa consiste en una colección de axiomas y reglas. Los sistemas de programación lógicos (como Prolog) calculan las consecuencias de los axiomas y las reglas organizadas para responder a una consulta.
Hoy en día, la lógica es extensamente aplicada en los campos de inteligencia artificial y de ciencias de computación, y estos campos proporcionan una rica fuente de problemas en la lógica formal e informal. La teoría de la argumentación es un buen ejemplo de cómo la lógica está siendo aplicada a la inteligencia artificial. El sistema de clasificación computacional ACM, en particular, considera:
- Sección F.3 en Lógicas y significados de programas y F.4 en Lógica matemática y lenguajes formales como parte de la teoría de la ciencia de computación: este trabajo cubre la semántica formal de los lenguajes de programación tan bien como el trabajo de métodos formales como la lógica de Hoare.
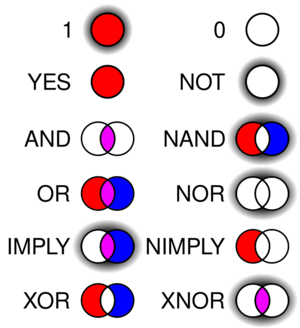
- Lógica booleana como fundamento en el hardware de la computadora, particularmente la sección del sistema B.2 en la estructura aritmética y lógica, relacionado con operadores AND, NOT y OR.
- Muchos formalismos lógicos fundamentales son esenciales para la sección I.2 sobre inteligencia artificial, por ejemplo la lógica modal y la lógica por defecto en los formalismos y métodos de representación del conocimiento, las cláusulas de Horn en la programación lógica y la lógica de descripción.
Además, las computadoras se pueden usar como herramientas para los lógicos. Por ejemplo, en lógica simbólica y lógica matemática, las pruebas de los seres humanos pueden ser asistidas por computadoras. Usando la prueba automatizada del teorema, las máquinas pueden encontrar y comprobar pruebas, así como trabajar con las pruebas demasiadas largas como para escribir a mano.
La lógica computacional es la aplicación de la lógica matemática al mundo de las computadoras. Es esencial para diseñar los circuitos de una computadora, para crear programas (especialmente en la programación lógica) y para hacer que los algoritmos funcionen de manera eficiente.
Gracias a la lógica, los científicos han podido pensar en cómo las máquinas podrían "razonar" o tener inteligencia artificial. Aunque el razonamiento humano es complejo, la lógica ayuda a construir sistemas que pueden procesar información y tomar decisiones. Las computadoras también pueden ayudar a los expertos en lógica a verificar argumentos muy largos o complejos.
Lógica filosófica: el estudio del razonamiento en la filosofía
Entendida en un sentido estricto, la lógica filosófica es el área de la filosofía que estudia la aplicación de métodos lógicos a problemas filosóficos, a menudo en forma de sistemas lógicos extendidos como la lógica modal. Algunos teóricos conciben la lógica filosófica en un sentido más amplio como el estudio del alcance y la naturaleza de la lógica en general. En este sentido, la lógica filosófica puede considerarse idéntica a la filosofía de la lógica, que incluye temas adicionales como la definición de la lógica o la discusión de los conceptos fundamentales de la lógica. El presente artículo trata la lógica filosófica en el sentido estricto, en el que constituye un campo de investigación dentro de la filosofía de la lógica.
Un tema importante para la lógica filosófica es la cuestión de cómo clasificar la gran variedad de sistemas lógicos no clásicos, muchos de los cuales son de origen bastante reciente. Una forma de clasificación que se encuentra a menudo en la literatura es distinguir entre lógicas extendidas y lógicas desviadas. La lógica misma puede definirse como el estudio de la inferencia válida. La lógica clásica es la forma dominante de la lógica y articula reglas de inferencia de acuerdo con intuiciones lógicas compartidas por muchos, como el principio del tercero excluido, la eliminación de la doble negación y la bivalencia de la verdad.
Las lógicas extendidas son sistemas lógicos que se basan en la lógica clásica y sus reglas de inferencia, pero la extienden a nuevos campos introduciendo nuevos símbolos lógicos y las correspondientes reglas de inferencia que rigen estos símbolos. En el caso de la lógica modal alética, estos nuevos símbolos se utilizan para expresar no solo lo que es verdadero simpliciter, sino también lo que es posible o necesariamente verdadero. A menudo se combina con la semántica de los mundos posibles, que sostiene que una proposición es posiblemente verdadera si es verdadera en algún mundo posible, mientras que es necesariamente verdadera si es verdadera en todos los mundos posibles. La lógica deóntica pertenece a la ética y proporciona un tratamiento formal de las nociones éticas, como la obligación y el permiso. La lógica temporal formaliza las relaciones temporales entre proposiciones. Esto incluye ideas como si algo es verdadero en algún momento o todo el tiempo y si es verdadero en el futuro o en el pasado. La lógica epistémica pertenece a la epistemología. Puede usarse para expresar no solo lo que es el caso, sino también lo que alguien cree o sabe que es el caso. Sus reglas de inferencia articulan lo que se desprende del hecho de que alguien tiene estos tipos de estados mentales. Las lógicas de orden superior no aplican directamente la lógica clásica a ciertos subcampos nuevos dentro de la filosofía, sino que la generalizan al permitir la cuantificación no solo sobre individuos sino también sobre predicados.
Las lógicas desviadas, en contraste con estas formas de lógicas extendidas, rechazan algunos de los principios fundamentales de la lógica clásica y a menudo son vistas como sus rivales. La lógica intuicionista se basa en la idea de que la verdad depende de la verificación a través de una prueba. Esto la lleva a rechazar ciertas reglas de inferencia encontradas en la lógica clásica que no son compatibles con esta suposición. La lógica libre modifica la lógica clásica para evitar los presupuestos existenciales asociados al uso de términos singulares posiblemente vacíos, como nombres y descripciones definidas. Las lógicas plurivalentes permiten valores de verdad adicionales además de verdadero y falso. Por lo tanto, rechazan el principio de bivalencia de la verdad. Las lógicas paraconsistentes son sistemas lógicos capaces de lidiar con contradicciones. Lo hacen evitando el principio de explosión que se encuentra en la lógica clásica. La lógica relevante es una forma prominente de lógica paraconsistente. Rechaza la interpretación puramente funcional de verdad del condicional material al introducir el requisito adicional de relevancia: para que el condicional sea verdadero, su antecedente tiene que ser relevante para su consecuente.
La lógica filosófica es la parte de la filosofía que usa los métodos de la lógica para resolver preguntas filosóficas. Por ejemplo, estudia cómo podemos razonar sobre lo que es "posible" o "necesario", o sobre lo que "deberíamos" hacer.
También explora diferentes tipos de lógica que van más allá de la lógica clásica, como las lógicas que permiten más de dos valores de verdad (no solo verdadero o falso) o las que pueden manejar contradicciones.
Lógica informal: el arte de argumentar en la vida diaria
La lógica informal, o lógica no formal, es el estudio de los argumentos a posteriori en oposición al estudio técnico y teórico de la lógica matemática o lógica formal. Esta parte de la lógica se dedica principalmente a diferenciar entre formas correctas e incorrectas en que se desarrolla el lenguaje y el pensamiento cotidiano, en especial al estudio de los procesos para obtener conclusiones a partir de información dada, sin importar su forma lógica. Parte de que el pensamiento y el lenguaje humano es a menudo incorrecto, o tendencioso. Surgió en la década de los años 1970 como un subcampo de la filosofía. La primera obra en hablar acerca de esta disciplina fue La lógica y la retórica contemporánea (1971) de Howard Kahane.
La lógica informal se enfoca en cómo usamos el razonamiento y el lenguaje en nuestra vida diaria. Nos ayuda a identificar si un argumento es bueno o malo, incluso si no sigue reglas matemáticas estrictas. Esta lógica es muy útil para entender debates, noticias y conversaciones, y para mejorar nuestra forma de comunicarnos.
Lógica silogística: los inicios del razonamiento formal
La lógica silogística fue desarrollada por el filósofo griego Aristóteles. Es uno de los primeros sistemas de lógica formal. Se basa en los silogismos, que son argumentos con dos ideas iniciales (premisas) y una conclusión.
Por ejemplo:
- Todos los hombres son mortales.
- Sócrates es un hombre.
- Por lo tanto, Sócrates es mortal.
Aunque es un sistema antiguo, sentó las bases para el estudio de la lógica y todavía se usa para analizar ciertos tipos de argumentos.
Lógica proposicional: combinando afirmaciones
La lógica proposicional es un sistema formal donde las afirmaciones completas (proposiciones) se combinan usando conectores lógicos como "y", "o", "si... entonces...", "no". A diferencia de otros tipos de lógica, aquí la unidad más pequeña es una afirmación completa que puede ser verdadera o falsa.
Por ejemplo, si "P" significa "Está lloviendo" y "Q" significa "El suelo está mojado", podemos combinarlas para formar "Si P, entonces Q" (Si está lloviendo, entonces el suelo está mojado).
Lógica modal: más allá de lo verdadero y falso
La lógica modal estudia cómo las palabras como "posible", "necesario", "debe" o "puede" cambian el significado de una frase. Por ejemplo, no es lo mismo decir "Vamos a los juegos" que "Debemos ir a los juegos".
Esta lógica nos ayuda a entender diferentes tipos de posibilidades y necesidades. También se usa para hablar sobre el tiempo (si algo es verdadero ahora, en el futuro o en el pasado) y sobre lo que las personas creen o saben.
Lógica de predicados: analizando detalles
La lógica de predicados es un sistema más avanzado que la lógica proposicional. Permite analizar las oraciones en partes más pequeñas, como sujetos y propiedades. También puede manejar ideas como "para todos" o "existe al menos uno".
Por ejemplo, puede expresar ideas como "Todos los perros son mamíferos" o "Existe un número que es par". Esta lógica es fundamental para la lógica matemática moderna y para la inteligencia artificial.
Lógica no clásica: desafiando las reglas
Las lógicas no clásicas son sistemas que cambian o rechazan algunas de las reglas básicas de la lógica clásica. Por ejemplo, algunas lógicas no clásicas permiten más de dos valores de verdad (no solo verdadero o falso), o pueden manejar situaciones donde hay contradicciones sin que todo el sistema se derrumbe.
Un ejemplo es la lógica difusa, que permite "grados de verdad" entre 0 y 1, como cuando decimos que algo es "un poco" verdadero o "bastante" falso.
Historia de la lógica
La historia de la lógica documenta el desarrollo de la lógica en varias culturas y tradiciones a lo largo de la historia. Aunque muchas culturas han empleado intrincados sistemas de razonamiento, e, incluso, el pensamiento lógico estaba ya implícito en Babilonia en algún sentido, la lógica como análisis explícito de los métodos de razonamiento ha recibido un tratamiento sustancial solo originalmente en tres tradiciones: la Antigua China, la Antigua India y la Antigua Grecia.
Aunque las dataciones exactas son inciertas, particularmente en el caso de la India, es probable que la lógica emergiese en las tres sociedades hacia el siglo IV a. C. El tratamiento formalmente sofisticado de la lógica proviene de la tradición griega, especialmente del Organon aristotélico, cuyos logros serían desarrollados por los lógicos islámicos y, luego, por los lógicos de la Edad Media europea. El descubrimiento de la lógica india entre los especialistas británicos en el siglo XVIII influyó también en la lógica moderna.
La historia de la lógica es producto de la confluencia de cuatro líneas de pensamiento, que aparecen en momentos históricos diferentes: La lógica aristotélica, seguida de los aportes de los megáricos y los estoicos. Siglos después, Ramon Llull y Leibniz estudiaron la posibilidad de un lenguaje único, completo y exacto para razonar. Al comienzo del siglo XIX las investigaciones en los fundamentos del álgebra y la geometría, seguidos por el desarrollo del primer cálculo completo por Frege. Ya en el siglo XX, Bertrand Russell y Whitehead culminaron el proceso de creación de la lógica matemática. A partir de este momento no cesarán de producirse nuevos desarrollos y de nacer escuelas y tendencias. Otra perspectiva interesante sobre cómo abordar el estudio de la historia lógica la ofrece Alberto Moretti y que es sintetizada por Diego Letzen.
La lógica tiene una historia muy larga. Surgió de forma independiente en diferentes culturas antiguas, como China, India y Grecia, alrededor del siglo IV a.C.
En Grecia, el filósofo Aristóteles fue muy importante. Sus escritos sobre lógica, conocidos como el Organon, fueron la base de la lógica durante muchos siglos. Sus ideas fueron estudiadas y desarrolladas por pensadores en el mundo islámico y en Europa durante la Edad Media.
Más tarde, en el siglo XIX, la lógica empezó a transformarse con el trabajo de matemáticos como Gottlob Frege, quien creó un sistema de lógica formal muy completo. En el siglo XX, figuras como Bertrand Russell y Alfred North Whitehead continuaron desarrollando la lógica matemática, lo que llevó a la lógica a ser una parte fundamental de las matemáticas y la informática.
Galería de imágenes
-
Esquema del modus ponens, una regla de inferencia fundamental de la lógica proposicional.
-
El cubo imposible es un objeto paradójico.
-
Gottlob Frege's Begriffschrift introduced the notion of quantifier in a graphical notation, which here represents the judgement that
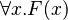 is true.
is true.
Véase también
 En inglés: Logic Facts for Kids
En inglés: Logic Facts for Kids