Metalógica para niños
La metalógica es una rama de la lógica que se encarga de estudiar las características y partes de los sistemas formales. Piensa en la lógica como un juego con reglas. La metalógica es la parte que estudia esas reglas del juego y cómo funciona el juego en sí.
Algunas de las características más importantes que se pueden analizar en los sistemas formales son la consistencia, la decidibilidad y la completitud. Ejemplos de descubrimientos importantes en metalógica son los teoremas de incompletitud de Gödel, el teorema de completitud de Gödel y el teorema de Löwenheim-Skolem. Otra característica importante es la compacidad.
Contenido
Propiedades de los Sistemas Lógicos
Mientras que la lógica matemática se dedica a crear sistemas lógicos, la metalógica se ocupa de analizar las características de esos sistemas. Las propiedades más importantes que se pueden estudiar en los sistemas lógicos son:
¿Qué es la Consistencia en Lógica?
En metalógica, la consistencia o consistencia lógica es la propiedad que tienen los sistemas formales cuando no es posible deducir una contradicción dentro del sistema. Es decir, dado un lenguaje formal y un aparato deductivo (axiomas y reglas de inferencia), no es posible deducir una fórmula y su negación. La existencia de un modelo implica que una teoría lógica es consistente.
Generalizando, la consistencia es una propiedad que pueden tener los conjuntos de fórmulas. Intuitivamente, un conjunto de fórmulas es consistente cuando no es posible deducir una contradicción del mismo. Es decir, dado un lenguaje formal y un aparato deductivo, no es posible demostrar una fórmula y su negación. Equivalentemente, esto se puede expresar diciendo que para ninguna proposición lógica p: 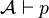 y
y 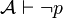 simultáneamente.
simultáneamente.
Un sistema lógico es consistente si no puede probar algo y su opuesto al mismo tiempo. Imagina que las reglas de un juego no te permiten decir que una ficha está en dos lugares diferentes a la vez. Si un sistema es consistente, significa que sus reglas no llevan a contradicciones.
¿Qué es la Decidibilidad en Lógica?
En metalógica, la decidibilidad es una propiedad de los sistemas formales cuando, para cualquier fórmula en el lenguaje del sistema, existe un método efectivo para determinar si esa fórmula pertenece o no al conjunto de las verdades del sistema. Por ejemplo, la lógica proposicional es decidible, porque existe un algoritmo (la tabla de verdad) que en un número finito de pasos puede decidir si la fórmula es válida o no.
Cuando una fórmula no puede ser probada verdadera ni falsa, se dice que la fórmula es independiente, y que por lo tanto el sistema es no decidible. La única manera de incorporar una fórmula independiente a las verdades del sistema es postulándola como axioma. Dos ejemplos muy importantes de fórmulas independientes son el axioma de elección en la teoría de conjuntos, y el quinto postulado de la geometría euclidiana.
Un sistema es decidible si siempre hay un método claro y que termina en un número finito de pasos para saber si una afirmación es verdadera o falsa dentro de ese sistema. Por ejemplo, en la lógica proposicional, podemos usar una tabla de verdad para decidir si una afirmación es válida.
Si una afirmación no puede ser probada como verdadera ni como falsa, se dice que es independiente. En ese caso, el sistema no es decidible para esa afirmación.
¿Qué es la Completitud en Lógica?
En metalógica, la completitud o completud semántica es la propiedad metateórica que tienen los sistemas formales cuando todas las fórmulas lógicamente válidas (todas las verdades lógicas) del sistema son además teoremas del sistema. Es decir, cuando el conjunto de las verdades lógicas del sistema es un subconjunto del conjunto de teoremas. En otras palabras, si A es una fórmula cualquiera del lenguaje y S es el sistema formal bajo consideración, entonces se cumple que:
- Si
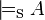 entonces
entonces 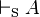
Por otra parte, la completitud sintáctica es la propiedad que tienen los sistemas formales cuando, para toda fórmula cerrada del lenguaje del sistema, o bien es un teorema o bien su negación lo es. Esto es, existe una prueba para cada fórmula cerrada o para su negación.
La lógica proposicional y la lógica de primer orden son ambas semánticamente completas, pero no sintácticamente completas. Por ejemplo, en la lógica proposicional, la fórmula p no es un teorema, y tampoco lo es su negación, de modo que eso basta para mostrar que no es sintácticamente completa. No obstante, como ninguna de esas dos fórmulas es una verdad lógica, no afectan a la completitud semántica del sistema.
El segundo teorema de incompletitud de Gödel demuestra que ningún sistema (definido recursivamente) con cierto poder expresivo puede ser a la vez consistente y sintácticamente completo.
Otra propiedad metateórica distinta es la completitud semántica fuerte, que dice: si en un sistema formal S, A es una fórmula bien formada cualquiera que es una consecuencia semántica de un conjunto 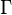 de fórmulas, entonces existe una derivación de A a partir de
de fórmulas, entonces existe una derivación de A a partir de 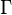 . En símbolos:
. En símbolos:
- Si
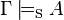 entonces
entonces 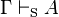
Un sistema es completo si todas las afirmaciones que son verdaderas dentro de ese sistema también pueden ser probadas usando sus reglas. Es como si en un juego, todas las jugadas correctas pudieran ser demostradas siguiendo las reglas.
Existen dos tipos de completitud:
- Completitud semántica: Significa que todo lo que es lógicamente verdadero en el sistema puede ser probado.
- Completitud sintáctica: Significa que para cualquier afirmación, o bien esa afirmación es un teorema (se puede probar), o su negación es un teorema.
La lógica proposicional y la lógica de primer orden son semánticamente completas, pero no sintácticamente completas. Los teoremas de incompletitud de Gödel muestran que ningún sistema lo suficientemente complejo puede ser a la vez consistente y sintácticamente completo.
¿Qué es la Compacidad en Lógica?
En lógica matemática, el teorema de compacidad establece que un conjunto (posiblemente infinito) de fórmulas bien formadas de la lógica de primer orden tiene un modelo si todos sus subconjuntos finitos tienen un modelo. Es decir, para todo conjunto de fórmulas 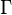 de un lenguaje L, si todo subconjunto finito de
de un lenguaje L, si todo subconjunto finito de 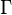 es satisfacible, entonces
es satisfacible, entonces 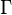 es satisfacible.
es satisfacible.
La lógica proposicional como la lógica de primer orden satisfacen el teorema de compacidad. Es decir, si de un conjunto de proposiciones se sigue una consecuencia, entonces existe un subconjunto finito de proposiciones de las cuales se sigue la misma conclusión. Análogamente si cada conjunto finito de proposiciones de un conjunto admite un modelo, entonces el conjunto completo admite un modelo. Si bien la lógica de primer orden tiene compacidad en el sentido previamente explicado, otras lógicas "más potentes" como la lógica de segundo orden no tienen la propiedad de compacidad.
La compacidad es una propiedad que dice que si un grupo muy grande de afirmaciones lógicas tiene sentido (es decir, tiene un "modelo" o una forma de ser verdaderas), entonces cualquier parte más pequeña de ese grupo también tiene sentido. Es como si un rompecabezas gigante tiene solución, entonces cualquier pieza pequeña que tomes de ese rompecabezas también encaja en algún lugar.
Descubrimientos Metalógicos Importantes
Teoremas de Incompletitud de Gödel

Los teoremas de incompletitud de Gödel son dos célebres teoremas de lógica matemática demostrados por Kurt Gödel en 1931. Ambos están relacionados con la existencia de proposiciones indecidibles en ciertas teorías aritméticas.
Estos son dos teoremas muy famosos de la lógica matemática que fueron demostrados por Kurt Gödel en 1931. Básicamente, muestran que en cualquier sistema lógico lo suficientemente complejo (como el que usamos para la aritmética), siempre habrá afirmaciones que no se pueden probar como verdaderas ni como falsas dentro de ese mismo sistema. Es como si en un juego de reglas muy complicado, hubiera preguntas que las propias reglas del juego no pueden responder.
Teorema de Löwenheim-Skolem
En lógica matemática, el teorema de Löwenheim-Skolem o teorema de Löwenheim-Skolem-Tarski es un teorema que establece que si una teoría de primer orden es consistente, entonces tiene al menos un modelo con dominio finito o numerable. Más precisamente: sea T un subconjunto consistente de un lenguaje de primer orden ℒ (con identidad): si T es finito o numerable, entonces tiene al menos un modelo con dominio finito o numerable. Esto significa que las teorías de primer orden no pueden controlar la cardinalidad de sus modelos: ninguna teoría consistente puede tener sólo modelos isomórficos.
La primera versión del teorema se debe a Leopold Löwenheim en 1915, aunque su demostración tenía una pequeña laguna. Thoralf Skolem demostró una segunda versión del teorema en 1919. Desde entonces han aparecido otras versiones.
Skolem comprendió que este teorema se podría aplicar para las formalizaciones de primer orden de la teoría de conjuntos, siendo dicha formalización numerable, existiría un modelo numerable para dicha teoría aun cuando la teoría afirma que existen conjuntos no contables. Este resultado contraintuitivo es la conocida paradoja de Skolem.
En general el teorema de Löwenheim-Skolem no se sostiene en lógicas más fuertes, como la lógica de segundo orden.
Este teorema, desarrollado por Leopold Löwenheim en 1915 y Thoralf Skolem en 1919, dice que si un sistema lógico de "primer orden" es consistente (no tiene contradicciones), entonces siempre puede tener un modelo (una forma de que sus afirmaciones sean verdaderas) que sea finito o que se pueda contar (como los números enteros). Esto significa que los sistemas de primer orden no pueden controlar el tamaño de sus modelos.
Un ejemplo curioso de esto es la paradoja de Skolem, que muestra cómo la teoría de conjuntos (que habla de conjuntos infinitos) puede tener un modelo que se puede contar.
Teorema de Completitud de Gödel
El teorema de completitud de Gödel es un importante teorema de la lógica matemática, que fue demostrado por primera vez por Kurt Gödel en 1929 y que en su forma más conocida establece lo siguiente:
|
La palabra «demostrable» significa que existe una deducción formal de la fórmula. La deducción consiste en una lista finita de pasos en los que cada paso o bien invoca a un axioma o es obtenido a partir de pasos previos mediante una básica regla de inferencia. A partir de dicha deducción, es posible verificar si cada uno de los pasos es correcto mediante un algoritmo (por ejemplo, mediante una computadora o a mano).
Una fórmula es lógicamente válida si es verdadera en todo modelo para el lenguaje utilizado en la fórmula. Para expresar de manera formal el teorema de completitud de Gödel, se debe definir el significado de la palabra modelo en este contexto. Esta es una definición básica en la teoría de modelos.
El teorema de Gödel establece una correspondencia entre la verdad semántica y la probabilidad sintáctica en la lógica de primer orden. Crea un vínculo entre la teoría de modelos que se ocupa de lo que es cierto en diferentes modelos, y la teoría de la demostración que estudia lo que se puede probar formalmente en sistemas formales particulares. Gödel utilizó el teorema de completitud para probar el teorema de compacidad, demostrando la naturaleza finitaria del operador de consecuencia lógica. Estos resultados ayudaron a establecer la lógica de primer orden como el tipo de lógica dominante en las matemáticas actuales.
Fue luego simplificado en 1947, cuando Leon Henkin observó en su tesis de doctorado que la parte difícil de la prueba se puede presentar como el Modelo de Teorema de la Existencia (publicado en 1949). A su vez, la prueba de Henkin fue simplificada por Gisbert Hasenjaeger en 1953.
Este es otro teorema muy importante de la lógica matemática, demostrado por Kurt Gödel en 1929. Dice que en la lógica de primer orden, si una afirmación es verdadera en todos los casos posibles (es "válida"), entonces también se puede probar usando las reglas de ese sistema.
"Demostrable" significa que hay una serie de pasos lógicos que te llevan a esa afirmación, como una receta. Este teorema conecta lo que es "verdadero" con lo que se puede "probar" en lógica.
Otros Descubrimientos Importantes
- La consistencia de la lógica proposicional (Emil Post 1920).
- La completitud semántica de la lógica proposicional (Paul Bernays 1918, Emil Post 1920).
- La decidibilidad de la lógica proposicional (Emil Post 1920).
- La consistencia de la lógica de primer orden monádica (Leopold Löwenheim 1915).
- La completitud semántica de la lógica de primer orden monádica (Leopold Löwenheim 1915).
- La decidibilidad de la lógica de primer orden monádica (Leopold Löwenheim 1915).
- La consistencia de la lógica de primer orden (David Hilbert y Wilhelm Ackermann 1928).
- La indecidibilidad de la lógica de primer orden (Entscheidungsproblem, Alonzo Church 1936 y Alan Turing 1936).
Véase también
 En inglés: Metalogic Facts for Kids
En inglés: Metalogic Facts for Kids