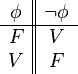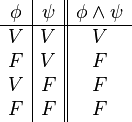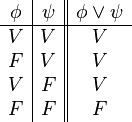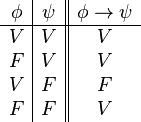robot de la enciclopedia para niños

Lógica proposicional para niños

Enciclopedia para niños

La lógica proposicional es como un juego de construcción de ideas. Nos ayuda a entender cómo se conectan las frases o "proposiciones" para formar argumentos más grandes. Imagina que cada frase simple es un bloque de construcción. La lógica proposicional nos enseña a usar "pegamentos" especiales, llamados conectivas lógicas, para unir esos bloques y ver si el resultado es una idea sólida y verdadera.

Esta lógica no se fija en lo que significan las frases por dentro, sino en cómo se unen. Por ejemplo, no le importa si "el cielo es azul" es verdad o no, solo le importa si esa frase se une con "está lloviendo" usando un "y" o un "o".

Una característica importante es que cada frase simple (o proposición) puede ser solo verdadera o falsa. No hay puntos intermedios. Esto hace que la lógica proposicional sea muy clara y nos permita saber si un argumento es correcto en pocos pasos.

¿Qué es la Lógica Proposicional?

La lógica proposicional nos ayuda a analizar si un argumento es válido. Un argumento es un conjunto de frases, donde algunas son las "premisas" (lo que se asume como cierto) y otra es la "conclusión" (lo que se deduce de las premisas).

Entendiendo los Argumentos Lógicos

Veamos un ejemplo sencillo:

  1. Mañana es miércoles o mañana es jueves.
  2. Mañana no es jueves.
  3. Por lo tanto, mañana es miércoles.

Este argumento es válido. Esto significa que si las primeras dos frases (premisas) son verdaderas, entonces la tercera frase (conclusión) también debe ser verdadera. Es imposible que las premisas sean ciertas y la conclusión falsa.

La validez de este argumento no depende de si realmente es miércoles o jueves. Depende de cómo se usan las palabras "o" y "no". Si cambiamos esas palabras, el argumento podría dejar de ser válido.

Por ejemplo:

  1. Ni está soleado ni está nublado.
  2. No está nublado.
  3. Por lo tanto, está soleado.

Este último argumento no es válido. Las palabras "ni... ni" cambian el significado.

Variables y Conectivas Lógicas

Para estudiar estos argumentos de forma más sencilla, la lógica proposicional usa símbolos. Las frases simples, como "mañana es miércoles" o "está nublado", se reemplazan por letras, como p, q, r, etc. A estas letras se les llama variables proposicionales.

Las palabras como "o", "no", "y", que unen las frases, se llaman conectivas lógicas. Son como los operadores matemáticos (+, -, x, /) pero para las ideas.

Así, el primer argumento se vería así:

  1. p o q
  2. No q
  3. Por lo tanto, p

Conectivas Lógicas Principales

Las conectivas lógicas son como funciones que toman valores de verdad (verdadero o falso) y devuelven otro valor de verdad. Cada conectiva tiene un comportamiento único.

Aquí están las conectivas más importantes:

Conectiva Expresión en el
lenguaje natural		 Ejemplo Símbolo
Negación no No está lloviendo. \neg \,
Conjunción y Está lloviendo y está nublado. 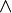\land
Disyunción o Está lloviendo o está soleado. \lor
Condicional material si... entonces Si está soleado, entonces es de día. \to \,
Bicondicional si y solo si Está nublado si y solo si hay nubes visibles. \leftrightarrow

Tablas de Verdad

Las tablas de verdad nos muestran cómo se comporta cada conectiva. Nos dicen si una frase combinada es verdadera o falsa, dependiendo de si las frases que la forman son verdaderas (V) o falsas (F).

Negación Conjunción Disyunción Condicional Bicondicional

\begin{array}{c||c} \phi & \neg \phi \\ \hline F & V \\ V & F \\ \end{array}

\begin{array}{c|c||c} \phi & \psi & \phi \land \psi \\ \hline V & V & V \\ F & V & F \\ V & F & F \\ F & F & F \\ \end{array}

\begin{array}{c|c||c} \phi & \psi & \phi \lor \psi \\ \hline V & V & V \\ F & V & V \\ V & F & V \\ F & F & F \\ \end{array}

\begin{array}{c|c||c} \phi & \psi & \phi \to \psi \\ \hline V & V & V \\ F & V & V \\ V & F & F \\ F & F & V \\ \end{array}

\begin{array}{c|c||c} \phi & \psi & \phi \leftrightarrow \psi \\ \hline V & V & V \\ F & V & F \\ V & F & F \\ F & F & V \\ \end{array}
  • Negación (\neg \,): Si una frase es verdadera, su negación es falsa. Si es falsa, su negación es verdadera.
  • Conjunción (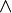\land): La frase combinada con "y" solo es verdadera si ambas frases son verdaderas.
  • Disyunción (\lor): La frase combinada con "o" es verdadera si al menos una de las frases es verdadera. Solo es falsa si ambas son falsas.
  • Condicional (\to \,): "Si... entonces". Es falsa solo si la primera parte es verdadera y la segunda es falsa. En todos los demás casos, es verdadera.
  • Bicondicional (\leftrightarrow): "Si y solo si". Es verdadera si ambas frases tienen el mismo valor de verdad (ambas verdaderas o ambas falsas).

Leyes Importantes en Lógica

Existen reglas o "leyes" que nos ayudan a entender cómo funcionan las conectivas. Algunas de las más conocidas son:

  • Ley de doble negación: Decir "no no p" es lo mismo que decir "p".
  • Leyes conmutativas: "p y q" es lo mismo que "q y p". "p o q" es lo mismo que "q o p".
  • Leyes de De Morgan: Nos ayudan a cambiar negaciones de "y" por "o" y viceversa. Por ejemplo, "no (p y q)" es lo mismo que "no p o no q".

Límites de la Lógica Proposicional

La lógica proposicional es muy útil, pero tiene sus límites. No puede analizar argumentos que dependen de la estructura interna de las frases.

Por ejemplo, considera este argumento:

  1. Todos los hombres son mortales.
  2. Sócrates es un hombre.
  3. Por lo tanto, Sócrates es mortal.

Este argumento es claramente válido. Sin embargo, si lo escribimos con variables proposicionales, se vería así:

  1. p
  2. q
  3. Por lo tanto, r

Desde el punto de vista de la lógica proposicional, esto no parece válido, porque no hay conectivas lógicas que lo unan. Para analizar este tipo de argumentos, necesitamos una lógica más avanzada, como la lógica de primer orden, que sí puede "mirar dentro" de las frases.

Historia de la Lógica Proposicional

La lógica es una de las ciencias más antiguas. Se cree que Aristóteles, un filósofo griego, fue el primero en estudiar la lógica de manera detallada hace muchísimos años. Él se enfocó en los "silogismos", que son un tipo de argumento con tres partes.

Mucho tiempo después, en el siglo III antes de Cristo, un filósofo llamado Crisipo de Solos desarrolló la lógica proposicional como un sistema formal. Él se centró en cómo las proposiciones (frases) se conectaban, lo cual era diferente de la lógica de Aristóteles.

Más tarde, en el siglo XII, Pedro Abelardo redescubrió y amplió estas ideas.

En los siglos XVII y XVIII, el matemático Gottfried Leibniz fue pionero en la "lógica simbólica", usando símbolos para representar ideas lógicas. Aunque su trabajo no fue muy conocido en su momento, otros lógicos como George Boole y Augustus De Morgan hicieron avances similares de forma independiente.

La lógica proposicional siguió evolucionando. Hoy en día, usamos herramientas como las tablas de verdad, que nos ayudan a visualizar los valores de verdad de las proposiciones. La invención de las tablas de verdad es un poco debatida, pero se atribuye a pensadores como Ludwig Wittgenstein y Emil Post.

La lógica proposicional es una base importante para entender cómo funciona el razonamiento y es fundamental en campos como la informática y la matemática.

Véase también

Kids robot.svg En inglés: Propositional logic Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Lógica_proposicional&oldid=5071300»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Lógica proposicional para Niños. Enciclopedia Kiddle.