Argumento para niños
Un argumento es una forma de expresar una idea o un razonamiento, ya sea hablando o escribiendo. Su objetivo es intentar demostrar, refutar o justificar algo. Piensa en ello como dar razones para apoyar lo que dices.
Las características más importantes de un buen argumento son que sea consistente y coherente. Esto significa que lo que dices debe tener sentido y estar bien conectado, como las piezas de un rompecabezas que encajan perfectamente.
Un argumento puede tener diferentes propósitos:
- Para mostrar la verdad: Que lo que dices sea cierto y encaje con otras verdades ya aceptadas, o que se base en hechos reales.
- Como un plan lógico: Que no tenga contradicciones, como en las matemáticas donde 2 + 2 siempre es 4.
- Para explicar una función: Que lo que se dice sea algo real y no solo una posibilidad.
- Para convencer a alguien: Para motivar a otra persona a hacer algo o a pensar de cierta manera.
- Para lograr una acción: Que lo que se dice sea coherente con los intereses de la persona que lo escucha, para que actúe de una forma específica.
Por lo tanto, un argumento se dirige a:
- La mente: Para "convencer" a alguien y que crea algo nuevo, usando la lógica y el conocimiento.
- Las emociones: Para "motivar" a alguien a realizar una acción.
- En el ámbito legal, un argumento se llama alegato y ayuda a encontrar la verdad en un juicio.
Contenido
¿Qué es un argumento?
En la lógica, un argumento se entiende como un grupo de ideas iniciales, llamadas premisas, seguidas de una conclusión. Un argumento puede ser muy fuerte (válido y con premisas verdaderas) o simplemente convincente. Pero no necesita ser perfecto para ser considerado un argumento.
Aquí tienes algunos ejemplos de argumentos válidos:
- Si hace sol, entonces es de día.
- Hace sol.
- Por lo tanto, es de día.
- Si no es martes, entonces es lunes.
- No es martes.
- Por lo tanto, es lunes.
- Los planetas giran alrededor del Sol.
- Marte es un planeta.
- Por lo tanto, Marte gira alrededor del Sol.
Para que un argumento sea válido, no es necesario que las premisas o la conclusión sean verdaderas en la vida real. Lo importante es que la conclusión se derive lógicamente de las premisas. Es decir, si las premisas fueran verdaderas, la conclusión también lo sería. Si un argumento es válido y además sus premisas son verdaderas, se dice que es un argumento sólido.
En un lenguaje más formal, como el de las matemáticas o la programación, un argumento es una secuencia de pasos o fórmulas. El último paso es la conclusión, y los anteriores son las premisas. Cada paso se obtiene de los anteriores siguiendo reglas claras. Una demostración matemática es un ejemplo de esto, donde se parte de ideas básicas (axiomas) y se llega a nuevas verdades (teoremas).
La ciencia y los argumentos
La ciencia es un gran ejemplo de cómo se usan los argumentos. En la ciencia, se usan oraciones para describir, definir y argumentar. El conocimiento científico se organiza siguiendo teorías y relaciones lógicas. Lo ideal es que estas relaciones sean tan precisas como las matemáticas.
A veces, la ciencia usa un lenguaje especial con símbolos, como en los cálculos lógicos o matemáticos. Esto ayuda a que las ideas sean muy claras y exactas.
Argumentos para resolver problemas
Cuando un argumento busca demostrar que una idea es verdadera, partiendo de otras ideas que ya se aceptan como ciertas, se le llama una prueba. Una prueba asegura que una nueva idea es verdadera dentro de un sistema de conocimiento.
Estos argumentos suelen ser deducciones, como las que hace un detective para resolver un misterio. El ejemplo más común es cuando planteamos y resolvemos problemas, por ejemplo, en matemáticas.
El argumento en las funciones matemáticas
En matemáticas, una función como  o
o 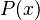 es como una forma vacía. Pero cuando la letra
es como una forma vacía. Pero cuando la letra  toma un valor específico, esa función cobra sentido. A ese valor que le damos a
toma un valor específico, esa función cobra sentido. A ese valor que le damos a  se le llama argumento de la función.
se le llama argumento de la función.
Por ejemplo:
| Ejemplo de una función matemática | Ejemplo de una función lógica |
|---|---|
La función 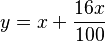 por sí sola no significa nada. Pero si por sí sola no significa nada. Pero si  es el precio de un artículo, por ejemplo 75 €, entonces la función calcula el precio final incluyendo un impuesto del 16%. Así, la función se vuelve real y puede ser verdadera o falsa en relación con el mundo. es el precio de un artículo, por ejemplo 75 €, entonces la función calcula el precio final incluyendo un impuesto del 16%. Así, la función se vuelve real y puede ser verdadera o falsa en relación con el mundo. |
Si  significa "ladrar" y significa "ladrar" y  es mi perro Desko, entonces es mi perro Desko, entonces 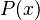 significa "Desko ladra". Esta frase puede ser verdadera o falsa dependiendo de si Desko está ladrando en ese momento. significa "Desko ladra". Esta frase puede ser verdadera o falsa dependiendo de si Desko está ladrando en ese momento. |
Argumentación en la vida diaria
La argumentación que usamos en el día a día es muy variada y se basa en muchas áreas, como el derecho, la filosofía, la comunicación y el lenguaje.
En la vida cotidiana, argumentar tiene mucho que ver con convencer a alguien de algo. Cuando argumentamos, buscamos que la otra persona cambie de opinión o acepte nuestra idea. Algunos expertos han estudiado cómo funciona esto.
El discurso para persuadir
Este tipo de argumento busca que, al escuchar las razones que se presentan, la otra persona actúe de la manera que se propone. Es un discurso que se dirige a la voluntad de las personas, para "persuadir" y moverlas a la acción con un propósito.
Aquí se mezclan el conocimiento y los intereses. Se usan palabras de forma inteligente para convencer, sin necesidad de decir mentiras.
Un ejemplo claro es el discurso de un político, un sermón religioso o la publicidad. En el ámbito legal, el alegato de un abogado defensor busca convencer al juez o al jurado a favor de su cliente.
Los expertos dicen que la capacidad de persuadir depende de varias cosas:
- La persona que argumenta: Si es confiable, tiene experiencia o es conocida.
- El mensaje: Si es emocional, lógico o una mezcla de ambos. También importa si el argumento es fuerte, novedoso, la cantidad de razones que se dan y qué tan importante es el mensaje.
- La persona que escucha: Su edad, su forma de pensar, su confianza en sí misma y su nivel de preocupación pueden influir en cómo recibe el mensaje.
Argumentos tipo prueba
Como ya mencionamos, estos son los argumentos lógicos y matemáticos. Son formales y se usan para demostrar una afirmación como una verdad necesaria e indiscutible. Esto sucede cuando todas las ideas del argumento, como en las matemáticas, llevan a una conclusión que es siempre verdadera.
A lo largo de la historia, ha habido varios argumentos importantes que han generado muchas discusiones:
- Argumento cosmológico (sobre el origen del universo)
- Argumento ontológico (sobre la existencia de Dios)
- Argumento analógico (comparando cosas similares)
- Argumento teleológico (sobre el propósito o diseño)
- Argumento hipotético-deductivo (basado en hipótesis y deducciones)
Falacias y no argumentos
Las falacias son tipos de argumentos o expresiones que parecen válidas, pero que en realidad tienen errores de razonamiento. Son como trucos lógicos que nos pueden engañar.
Un tipo de falacia ocurre cuando una palabra que normalmente indica una conclusión (como "por lo tanto") se usa solo para conectar ideas, sin que una se derive lógicamente de la otra. Por ejemplo: "Sócrates es un hombre, todos los hombres son mortales, por lo tanto, Sócrates es mortal" es un argumento válido, porque la conclusión se deduce de las premisas.
Sin embargo, "Tenía sed y, por lo tanto, bebí" no es un argumento. Aquí, "por lo tanto" solo indica que una cosa pasó después de la otra, no que "bebí" sea una consecuencia lógica de "tenía sed". Es una explicación, no un argumento lógico.
Véase también
 En inglés: Argument Facts for Kids
En inglés: Argument Facts for Kids
- Álgebra de Boole
- Argumento cosmológico
- Argumento hipotético-deductivo
- Dialéctica
- Evidencia
- Lógica
- Razonamiento
- Sofisma
- Falacia
- Filosofía
- Pensamiento crítico
- Política basada en evidencia
- Razonamiento abductivo
- Teorema de Bayes
- Teoría de la justificación
- Teoría de la argumentación
- Operando
- Silogismo
- Solidez

