Conjunto para niños
En matemáticas, un conjunto es como una colección o grupo de elementos que tienen algo en común. Imagina que tienes una caja y dentro de ella guardas objetos que comparten una característica. Esa caja con sus objetos es un conjunto.
Por ejemplo, el conjunto de los colores del arcoíris es:
- AI Plantilla:= {rojo, naranja, amarillo, verde, azul, añil, violeta}
Un conjunto se define por la característica que tienen todos sus elementos. Por ejemplo, el conjunto de los números primos (dentro de los números naturales) se define porque son números que solo se pueden dividir exactamente entre 1 y ellos mismos.
- P Plantilla:= {2, 3, 5, 7, 11, 13, …}
Contenido
¿Cómo surgieron los conjuntos?
La idea de los conjuntos como los conocemos hoy no se usó mucho en matemáticas hasta el siglo XIX. Fue entonces cuando los matemáticos empezaron a entender mejor el concepto de infinito.
Matemáticos como Bernard Bolzano y Bernhard Riemann ya tenían ideas parecidas a la de los conjuntos. Más tarde, Richard Dedekind usó ideas de conjuntos para explicar conceptos de álgebra, como las relaciones de equivalencia (cuando dos cosas están relacionadas de cierta manera) o las particiones (dividir algo en partes).
La teoría de conjuntos como un campo de estudio propio se le atribuye a Georg Cantor. Él empezó a investigar los conjuntos de números y luego se dedicó a estudiar los conjuntos infinitos y sus características. Gracias a Cantor y Dedekind, a finales del siglo XIX, los conjuntos se convirtieron en la base para construir muchos otros objetos matemáticos, como los números, las funciones y otras estructuras.
¿Qué es un conjunto?
Un conjunto es una colección de objetos que están bien definidos. Estos objetos pueden ser cualquier cosa: números, personas, letras, etc. Aquí tienes algunos ejemplos:
- A es el conjunto de los números naturales menores que 5.
- B es el conjunto de los colores verde, blanco y rojo.
- C es el conjunto de las vocales a, e, i, o y u.
- D es el conjunto de los palos de la baraja francesa.
Los conjuntos se suelen escribir con letras mayúsculas. Los objetos que forman un conjunto se llaman elementos o miembros. Decimos que un elemento "pertenece" a un conjunto usando el símbolo ∈. Por ejemplo, a ∈ A significa "a está en A" o "a pertenece a A". Si un elemento no pertenece, usamos el símbolo ∉.
Por ejemplo:
- 3 ∈ A (el número 3 está en el conjunto A).
- ♠ ∈ D (la pica está en el conjunto D).
- amarillo ∉ B (el color amarillo no está en el conjunto B).
- z ∉ C (la letra z no está en el conjunto C).
Formas de escribir conjuntos
Hay varias maneras de describir un conjunto.
- Por comprensión: Se describe una característica que todos los elementos del conjunto tienen en común. Por ejemplo, para el conjunto A (números naturales menores que 5) o D (palos de la baraja francesa).
- Por extensión: Se listan todos los elementos del conjunto. Por ejemplo, para los conjuntos B (verde, blanco, rojo) o C (a, e, i, o, u).
Es común usar llaves `{}` para escribir los elementos de un conjunto:
- B Plantilla:= {verde, blanco, rojo}
- C Plantilla:= {a, e, i, o, u}
También se usan llaves cuando se describe un conjunto por comprensión:
- A Plantilla:= {Números naturales menores que 5}
- D Plantilla:= {Palos de la baraja francesa}
Otra forma de escribir por comprensión es usando los dos puntos (`:`) o la barra vertical (`|`), que significan "tal que":
- A Plantilla:= {m : m es un número natural, y 1 ≤ m ≤ 5}
- F Plantilla:= {n2 : n es un entero y 1 ≤ n ≤ 10}
Esto significa que el conjunto F son los números que resultan de elevar al cuadrado un número entero entre 1 y 10. Es decir, los diez primeros cuadrados de números naturales.
¿Cuándo dos conjuntos son iguales?
Dos conjuntos son iguales si tienen exactamente los mismos elementos. No importa el orden en que se nombren los elementos, ni si se repiten.
Por ejemplo:
- El conjunto A de los números naturales menores que 5 es el mismo que el conjunto A′ de los números {1, 2, 3, 4}.
- B Plantilla:= {verde, blanco, rojo} Plantilla:= {colores de la bandera de México}
- B Plantilla:= {verde, blanco, rojo} Plantilla:= {rojo, verde, blanco} (El orden no importa).
- {1, 2} Plantilla:= {1, 2, 1} (Los elementos repetidos no cambian el conjunto).
El conjunto vacío
El conjunto que no tiene ningún elemento se llama conjunto vacío. Se representa con el símbolo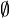 
o simplemente con llaves sin nada dentro: {}.
Solo existe un conjunto vacío. Es como una caja completamente vacía.
Características del conjunto vacío
Para cualquier conjunto A:
- El conjunto vacío es un subconjunto de cualquier conjunto A.
- Si unes un conjunto A con el conjunto vacío, el resultado es el mismo conjunto A.
- Si buscas los elementos que tienen en común un conjunto A y el conjunto vacío, el resultado es el conjunto vacío.
- El número de elementos del conjunto vacío es cero.
Subconjuntos
Un subconjunto es un conjunto que contiene algunos o todos los elementos de otro conjunto más grande.
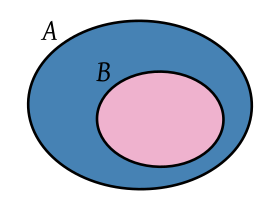
Un conjunto A es un subconjunto del conjunto B si cada elemento de A también es un elemento de B.
Se escribe A ⊆ B y se lee "A está contenido en B". También se puede escribir B ⊇ A, que significa "B contiene a A" o "B es un superconjunto de A".
Todo conjunto es un subconjunto de sí mismo. Por ejemplo, el conjunto de todas las personas es un subconjunto del conjunto de todas las personas.
Un subconjunto propio es un subconjunto que no es igual al conjunto original. Se escribe A ⊊ B. Por ejemplo:
- El "conjunto de todos los hombres" es un subconjunto propio del "conjunto de todas las personas".
- {1, 3} ⊊ {1, 2, 3, 4} (El conjunto {1, 3} es un subconjunto propio de {1, 2, 3, 4}).
- {1, 2, 3, 4} ⊆ {1, 2, 3, 4} (Este es un subconjunto, pero no propio).
Conjuntos disjuntos
Dos conjuntos son disjuntos si no tienen ningún elemento en común. Por ejemplo, el conjunto de los números racionales y el conjunto de los números irracionales son disjuntos, porque ningún número puede ser racional e irracional al mismo tiempo.
¿Cuántos elementos tiene un conjunto? (Cardinalidad)
Los conjuntos pueden ser finitos (si podemos contar sus elementos) o infinitos (si no podemos terminar de contarlos).
Para un conjunto finito, el número de elementos que tiene se llama su cardinal. El cardinal de un conjunto A se escribe como |A|, card(A) o #A.
- Si A es el conjunto de los números naturales menores que 5 ({1, 2, 3, 4}), entonces {{{1}}}.
- Si B es el conjunto de los colores {verde, blanco, rojo}, entonces {{{1}}}.
- El único conjunto con cardinal 0 es el conjunto vacío ∅.
En un conjunto infinito, como el de los números naturales (N Plantilla:= {1, 2, 3, …}), no hay un número finito de elementos. Aunque parezca extraño, algunos conjuntos infinitos pueden ser "más grandes" que otros. El "número de elementos" de un conjunto infinito se llama número transfinito.
Operaciones con conjuntos
Podemos combinar conjuntos de diferentes maneras para crear nuevos conjuntos. Estas son algunas operaciones básicas:
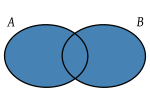
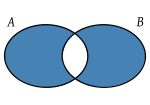
- Unión (símbolo ∪): La unión de dos conjuntos A y B es un nuevo conjunto que contiene todos los elementos que están en A, en B, o en ambos.
- Intersección (símbolo ∩): La intersección de dos conjuntos A y B es el conjunto de los elementos que están en ambos conjuntos al mismo tiempo.
- Diferencia (símbolo `\`): La diferencia del conjunto A con B es el conjunto que resulta de quitar de A cualquier elemento que también esté en B.
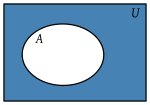
- Complemento (símbolo ∁): El complemento de un conjunto A es el conjunto de todos los elementos que no están en A, pero sí están en un conjunto más grande que los contiene a todos (llamado conjunto universal).
- Diferencia simétrica (símbolo Δ): La diferencia simétrica de dos conjuntos A y B es el conjunto de todos los elementos que están en A o en B, pero no en ambos a la vez.
- Producto cartesiano (símbolo ×): El producto cartesiano de dos conjuntos A y B es el conjunto de todas las parejas ordenadas (a, b), donde el primer elemento a es de A y el segundo elemento b es de B.
- Ejemplos de operaciones
- Unión: {1, a, 0} ∪ {2, b} Plantilla:= {2, b, 1, a, 0}
- Intersección: {5, z, ♠} ∩ {♠, a} Plantilla:= {♠}
- Diferencia: {5, z, ♠} \ {♠, a} Plantilla:= {5, z}
- Diferencia simétrica: {♠, 5} Δ {8, #, ♠} Plantilla:= {5, #, 8}
- Producto cartesiano: {1, a, 0} × {2, b} Plantilla:= {(1, 2), (1, b), (a, 2), (a, b), (0, 2), (0, b)}
Galería de imágenes
-
Los diversos polígonos en la imagen constituyen un conjunto. Algunos de los elementos del conjunto, además de ser polígonos son regulares. La colección de estos últimos —los polígonos regulares en la imagen— es otro conjunto, en particular, un subconjunto del primero.
Ver también
- Diagrama de Venn
- Función matemática
- Georg Cantor
- Número cardinal
- Relación matemática
- Teoría de conjuntos
Véase también
En inglés: Set Facts for Kids
