Lógica epistémica para niños
La lógica epistémica es una parte de la lógica modal que se encarga de estudiar cómo razonamos sobre el conocimiento. Imagina que quieres entender cómo las personas (o incluso las computadoras) saben cosas y cómo usan ese conocimiento. De eso se trata la lógica epistémica.
Aunque la idea de estudiar el conocimiento (llamada epistemología) existe desde hace mucho tiempo, la lógica epistémica es más reciente. Se usa en muchos campos, como la filosofía, la ciencia computacional, la inteligencia artificial, la economía y la lingüística.
Filósofos antiguos como Aristóteles ya hablaban de la lógica modal (que es la base de la lógica epistémica). Pero fue C.I. Lewis quien, en 1912, empezó a tratar este tema de forma más matemática y organizada. Luego, en 1963, el trabajo de Kripke le dio su forma moderna.
En la década de 1950, varios estudios mencionaron la lógica del conocimiento. Sin embargo, el libro An Essay in Modal Logic de von Wright, publicado en 1951, es considerado el inicio de este campo. Más tarde, en 1962, Hintikka escribió Knowledge and Belief, el primer trabajo extenso que propuso usar "modalidades" (formas de expresar posibilidad o necesidad) para entender el significado del conocimiento.
Desde entonces, la lógica epistémica ha avanzado mucho. Por ejemplo, se ha combinado con ideas de la lógica dinámica para crear lógicas que modelan cómo el conocimiento cambia en las conversaciones o cuando se actualiza la información.
Contenido
Cómo se modela el conocimiento
La mayoría de las veces, para entender el conocimiento, se usa un modelo llamado de los "mundos posibles". Piensa en esto como diferentes escenarios o situaciones que podrían ser reales.
Para usar este modelo, separamos los "mundos posibles" en dos grupos:
- Los que son compatibles con lo que una persona (o "agente") sabe.
- Los que no lo son.
Aunque hay diferentes maneras de hacer esto, la más común en lógica usa un enfoque basado en la lógica.
Estructuras de Kripke
El modelo principal para la lógica epistémica se basa en las estructuras de Kripke. Una estructura de Kripke es como un mapa que nos muestra:
- Un conjunto de "estados" o "mundos posibles" (diferentes situaciones).
- Una forma de saber qué afirmaciones son verdaderas en cada estado.
- Relaciones que nos dicen qué estados considera posibles cada agente.
Es importante entender que lo que es verdad puede cambiar de un "mundo" a otro. Que algo sea verdad en un mundo no significa que lo sea en todos.
Símbolos y lo que significan
El símbolo principal en lógica epistémica es la letra K. Se usa para decir "se sabe que" o "es consistente con lo que sabemos". Si hay varias personas, se le añade un número pequeño al lado, como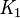 
o 
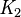, para indicar quién sabe qué. Así, 
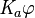significa "el agente 
sabe que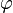 
(una afirmación)".
También hay símbolos para hablar del conocimiento en grupo:
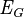: Significa "todos los agentes en el grupo G saben".
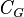: Significa "es conocimiento común en el grupo G". Esto quiere decir que todos lo saben, y saben que los demás lo saben, y así sucesivamente.
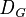: Significa "es conocimiento distribuido en el grupo G". Esto es lo que el grupo sabría si compartieran toda su información.
Características del conocimiento
Si asumimos que las personas son "razonadores perfectos" (es decir, siempre sacan las conclusiones lógicas correctas de lo que saben), podemos ver algunas propiedades interesantes del conocimiento.
Si sabes dos cosas, sabes su consecuencia
Imagina que sabes que "está lloviendo" y también sabes que "si llueve, entonces el suelo está mojado". Si sabes estas dos cosas, entonces lógicamente debes saber que "el suelo está mojado". Este principio se expresa así:
Si algo es siempre verdad, lo sabes
Si una afirmación es verdadera en todos los mundos posibles (es decir, es una verdad universal), entonces cualquier agente la sabe. Esto no significa que si algo es verdad, automáticamente lo sabes. Significa que si es una verdad que no puede ser de otra manera, entonces la conoces.
- si
entonces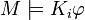 
Lo que sabes, es verdad
Esta es una característica clave del conocimiento: si sabes algo, ese algo debe ser verdad. No puedes "saber" algo que es falso. Puedes creer algo falso, pero no conocerlo.
Sabes lo que sabes
Esta propiedad dice que si sabes algo, también sabes que lo sabes. Por ejemplo, si sabes que 2 + 2 = 4, también sabes que sabes que 2 + 2 = 4.
Sabes lo que no sabes
Esta propiedad es un poco más compleja y dice que si no sabes algo, también sabes que no lo sabes. Por ejemplo, si no sabes la capital de un país lejano, sabes que no sabes esa capital.
Lógica de las creencias
La lógica epistémica también puede estudiar las creencias, no solo el conocimiento. En este caso, se usa el símbolo B en lugar de K. La diferencia principal es que puedes creer algo que no es verdad. Por eso, la propiedad "lo que sabes, es verdad" no se aplica a las creencias. En su lugar, se usa un principio que dice que un agente no cree en contradicciones. Esta parte de la lógica se llama lógica doxástica.
Véase también
En inglés: Epistemic modal logic Facts for Kids
- Epistemología
- Lógica computacional
