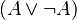Principio del tercero excluido para niños

El principio del tercero excluido, también conocido como principio del cuarto excluido o en latín tertium non datur (que significa "no se da una tercera opción"), es una idea fundamental en la lógica clásica. Fue propuesto por el famoso pensador Aristóteles.

Este principio nos dice que, si tenemos una afirmación y su opuesto (su negación), una de las dos debe ser verdadera y no hay una tercera posibilidad. Por ejemplo, si decimos "es de día" o "no es de día", una de las dos es cierta. No puede ser que no sea ni de día ni de noche. Otro ejemplo es: "Algo es blanco" o "Algo no es blanco".

El principio del tercero excluido es una de las leyes más importantes del pensamiento occidental, junto con el principio de no contradicción (que dice que algo no puede ser y no ser al mismo tiempo) y el principio de identidad (que dice que algo es igual a sí mismo).

En la lógica proposicional, que es una forma de estudiar cómo se conectan las ideas, este principio se puede representar así:

Aquí, la letra A representa cualquier afirmación, y el símbolo significa "o", mientras que significa "no". Así que la fórmula dice: "Una afirmación es verdadera O su negación es verdadera".

¿Qué diferencia hay entre juicios contradictorios y contrarios?

En la lógica de Aristóteles, se hace una distinción importante entre dos tipos de afirmaciones opuestas:

• Juicios contradictorios: Son afirmaciones que no pueden ser ciertas al mismo tiempo, y tampoco pueden ser falsas al mismo tiempo. No hay un punto intermedio. Por ejemplo, si decimos "Juan es bueno", su afirmación contradictoria es "Juan no es bueno". Una de las dos debe ser cierta, y no hay otra opción.
• Juicios contrarios: Son afirmaciones que no pueden ser ciertas al mismo tiempo, pero sí pueden ser falsas al mismo tiempo. Aquí sí puede haber un punto intermedio. Por ejemplo, "Juan es bueno" y "Juan es malo" son juicios contrarios. Juan no puede ser bueno y malo a la vez, pero podría ser "más o menos bueno" o "ni bueno ni malo", lo que sería un punto intermedio.

Algunos pensadores, como Stuart Mill, han señalado que hay frases que no son ni verdaderas ni falsas, sino que simplemente no tienen sentido. Por ejemplo, "abracadabra es una segunda intención" no es algo que podamos decir si es cierto o no, porque la frase en sí no tiene un significado claro.

Cuando un sistema de lógica no acepta el principio del tercero excluido, se crean las llamadas lógicas polivalentes. Estas lógicas permiten más de dos valores de verdad (no solo "verdadero" o "falso"), como "posible" o "indeterminado".

tampoco puede darse un término intermedio entre los contradictorios, sino que necesariamente se ha de afirmar o negar uno de ellos, sea el que sea, de una misma cosa.

Aristóteles, Metafísica, 1011b23-24

El principio del tercero excluido en las matemáticas

A lo largo de la historia, los matemáticos han estudiado cómo se aplica este principio en su campo.

La visión de L.E.J. Brouwer

El matemático L.E.J. Brouwer pensaba que este principio no siempre debería usarse en lógica. Él creía que, especialmente cuando se comparan conjuntos infinitos (grupos de cosas que no tienen fin), el principio del tercero excluido podría no ser válido. Para él, en matemáticas, a veces no es tan sencillo decir que algo es "verdadero" o "falso" sin más.

La respuesta de Barzin y Errera

Otros matemáticos, como Barzin y Errera, no estaban de acuerdo con Brouwer. Ellos demostraron que si se niega el principio del tercero excluido, se pueden llegar a contradicciones. Usaron un método llamado "reducción al absurdo", que consiste en asumir que algo es falso para ver si eso lleva a una contradicción, lo que probaría que la afirmación original era verdadera.

Un ejemplo para entenderlo mejor

Imaginemos la siguiente afirmación:

Sócrates es mortal.

Según el principio del tercero excluido, solo hay dos opciones posibles:

Sócrates es mortal, o Sócrates no es mortal.

Una de estas dos afirmaciones debe ser cierta. No tiene sentido decir que "Sócrates ni es mortal ni es inmortal", porque el principio excluye esa tercera opción. Por lo tanto, en la lógica clásica, solo una de las dos proposiciones puede ser considerada verdadera.

Sin embargo, es importante tener cuidado al aplicar este principio. Por ejemplo, si decimos:

Dublexi el Unicornio es mortal, o Dublexi el Unicornio no es mortal.

Según la lógica clásica, esto parece correcto. Pero la lógica moderna nos invita a preguntarnos primero: "¿Qué es un 'Dublexi el Unicornio'?" Si este nombre no se refiere a algo real o con sentido, entonces la pregunta en sí podría no tener una respuesta de "verdadero" o "falso", y el principio del tercero excluido no se aplicaría de la misma manera.

Galería de imágenes

• 

  Aristóteles, el filósofo que propuso este principio.

Véase también

En inglés: Law of excluded middle Facts for Kids