Baricentro para niños
En la física, el baricentro es como el punto de equilibrio de un objeto o de un sistema de objetos. Imagina que tienes una regla y quieres equilibrarla en tu dedo; el punto donde la equilibras es su baricentro. Si un objeto tiene la misma densidad en todas sus partes (es decir, es "homogéneo") o si su forma es muy simétrica, su baricentro coincide con su centro de masas. El baricentro es diferente del centroide en geometría, que es un punto de equilibrio para una forma plana, sin considerar su masa.
Cuando dos cuerpos, como un planeta y su luna, giran uno alrededor del otro, no giran exactamente alrededor del centro del más grande. En realidad, ambos giran alrededor de un punto llamado baricentro. Si uno de los cuerpos es mucho más grande que el otro y están cerca, el baricentro suele estar dentro del cuerpo más grande. Por ejemplo, en el sistema Tierra-Luna, el baricentro está dentro de la Tierra, a unos 4671 kilómetros de su centro. Esto es aproximadamente el 75% del radio de la Tierra. Por eso, parece que la Luna gira alrededor de la Tierra, y la Tierra solo se "tambalea" un poco.
Si los dos cuerpos tienen masas parecidas, el baricentro estará en algún punto entre ellos, y ambos girarán alrededor de ese punto. Un buen ejemplo es el sistema de Plutón y su luna Caronte. También ocurre con muchos asteroides dobles y estrellas dobles. A veces, si el cuerpo más pequeño está muy lejos, el baricentro puede estar fuera del cuerpo más grande. Esto sucede con Júpiter y el Sol. Aunque el Sol es mil veces más grande que Júpiter, la gran distancia entre ellos hace que su baricentro esté un poco fuera del Sol.
Contenido
¿Cómo se relaciona el baricentro con las órbitas?
El baricentro es un punto muy importante en la astronomía y la astrofísica. En un sistema de dos cuerpos que giran, el baricentro es uno de los puntos clave (llamados focos) de la órbita elíptica que cada cuerpo sigue. Si el baricentro está dentro del cuerpo más grande, este cuerpo parecerá "tambalearse" en lugar de seguir una órbita clara.
La distancia del centro del cuerpo más grande al baricentro depende de la distancia entre los dos cuerpos y de sus masas. Cuanto más masivo sea un cuerpo en comparación con el otro, más cerca estará el baricentro de él.
¿Cómo se calcula el baricentro?
Para calcular el baricentro de varios puntos, se usa una especie de "promedio ponderado". Imagina que cada punto tiene una "masa" asignada. El baricentro es el punto donde el sistema se equilibraría si esas masas estuvieran allí.
Si tienes varios puntos (A1, A2, ...) y cada uno tiene una "masa" (m1, m2, ...), puedes encontrar el baricentro (G) usando sus coordenadas. Por ejemplo, para la coordenada 'x' del baricentro (xG), sumas el producto de cada masa por su coordenada 'x' (m1*x1 + m2*x2 + ...) y divides el resultado entre la suma de todas las masas (m1 + m2 + ...).
Conceptos relacionados con el baricentro
¿Qué es un isobaricentro?
Un isobaricentro es un tipo especial de baricentro donde todas las "masas" de los puntos son iguales. En este caso, se suele considerar que todas las masas son 1. Si no se especifican las masas, por defecto se asume que es un isobaricentro.
Baricentro, centro de masa y centro de gravedad
Aunque a veces coinciden, el baricentro, el centro de gravedad y el centro de masas son conceptos diferentes:
- El centroide es un concepto puramente geométrico. Solo depende de la forma del objeto.
- El centro de masas depende de cómo está distribuida la materia en el objeto.
- El centro de gravedad depende de la fuerza de gravedad que actúa sobre el objeto.
Para que el centroide de un cuerpo sea igual a su centro de masas, el cuerpo debe tener una densidad uniforme o una forma muy simétrica. Para que el centro de masas sea igual al centro de gravedad, el cuerpo debe estar en un campo de gravedad que sea igual en todas partes.
Un objeto con una forma cóncava (como una medialuna o una herradura) puede tener su baricentro fuera de su propia forma.
¿Cómo encontrar el baricentro de un objeto?
Puedes encontrar el baricentro de un objeto de forma sencilla. Si tienes una figura recortada en cartulina y la cuelgas de un punto, girará hasta que su baricentro quede justo debajo del punto de donde la sujetas. Si dibujas una línea vertical desde el punto de sujeción y repites el proceso colgándola de otro punto, el baricentro estará donde se crucen las dos líneas.
Propiedades del baricentro
El baricentro tiene algunas propiedades interesantes:
- Homogeneidad: Si multiplicas todas las "masas" por el mismo número (que no sea cero), el baricentro no cambia de lugar.
- Asociatividad: Puedes calcular el baricentro por partes. Por ejemplo, si tienes tres puntos, puedes encontrar el baricentro de dos de ellos primero y luego usar ese resultado para encontrar el baricentro de los tres.
Ejemplos de cálculo
- Ejemplo 1
- El baricentro de un triángulo
El baricentro de un triángulo es el punto donde se cruzan sus medianas (líneas que van de un vértice al punto medio del lado opuesto). Si consideramos que cada vértice tiene la misma "masa", el baricentro estará en el segmento que une un vértice con el punto medio del lado opuesto, a un tercio de la distancia desde el punto medio.
- Ejemplo 2
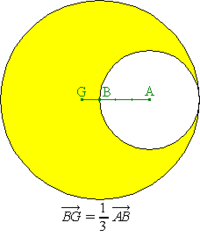
- El baricentro de una "medialuna"
Imagina una forma de "medialuna" hecha de cartón. Es como un círculo grande al que le quitamos un círculo más pequeño. Para encontrar su baricentro, podemos pensar que el círculo grande tiene una "masa" positiva y el círculo pequeño que quitamos tiene una "masa" negativa. Si el círculo grande tiene un radio doble que el pequeño, su área es cuatro veces mayor. Así, podríamos decir que el círculo grande tiene una "masa" de 4 y el pequeño una "masa" de -1. Con estos valores, podemos calcular el baricentro de la "medialuna".
¿Cómo se calcula el baricentro de un polígono?
Para encontrar el baricentro de un polígono (una figura con muchos lados), puedes dividirlo en triángulos y cuadriláteros más pequeños que no se superpongan. Luego, calculas el baricentro de cada una de esas figuras más pequeñas. Con esos baricentros, puedes encontrar el baricentro de todo el polígono. Este método es muy útil para figuras complejas.
Otros conceptos importantes
- Centro de gravedad
- Centro de masas
- Teorema del centroide de Pappus
- Centro geográfico
- Recta de Euler
- Ortocentro
- Circuncentro
- Incentro