Número e para niños
En matemáticas, la constante  es uno de los números irracionales y números trascendentes más importantes.
es uno de los números irracionales y números trascendentes más importantes.
Es aproximadamente 2,71828 y aparece en muchas áreas de las matemáticas. Es la base de los logaritmos naturales y se usa en ecuaciones de interés compuesto y otros problemas.
El número  , a veces llamado número de Euler o constante de Napier, fue reconocido por primera vez por el matemático escocés John Napier. Él introdujo la idea de logaritmo en el cálculo matemático.
, a veces llamado número de Euler o constante de Napier, fue reconocido por primera vez por el matemático escocés John Napier. Él introdujo la idea de logaritmo en el cálculo matemático.
Juega un papel clave en el cálculo y el análisis matemático. Es fundamental para definir la función exponencial, así como 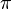 es importante para la geometría y el número
es importante para la geometría y el número 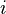 para el análisis complejo y el álgebra.
para el análisis complejo y el álgebra.
El número  , como
, como 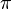 y el número áureo (φ), es un número irracional. Esto significa que no se puede escribir como una fracción de dos números enteros. Tampoco se puede representar con un número decimal exacto o un decimal que se repite. Además, al igual que
y el número áureo (φ), es un número irracional. Esto significa que no se puede escribir como una fracción de dos números enteros. Tampoco se puede representar con un número decimal exacto o un decimal que se repite. Además, al igual que 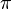 , es un número trascendente. Esto quiere decir que no es la solución de ninguna ecuación algebraica con números racionales. El valor de
, es un número trascendente. Esto quiere decir que no es la solución de ninguna ecuación algebraica con números racionales. El valor de  con sus primeras cifras decimales es:
con sus primeras cifras decimales es:
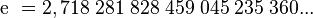
Datos para niños Lista de números – Números irracionalesγ – ζ(3) – √2 – √3 – √5 – φ – α – e – π – δ – τ |
|
| Binario | 10.10110111111000010101… |
| Decimal | 2.718281828459045235360… |
| Hexadecimal | 2.B7E151628AED2A6B… |
| Fracción continua | 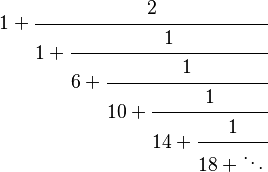 Nótese que la fracción continua no es periódica. |
Contenido
El Número e: Una Constante Matemática Especial
¿Qué es el número e?
El número e es una constante matemática muy importante. Su valor aproximado es 2.71828. Es un número irracional, lo que significa que sus decimales son infinitos y no se repiten en un patrón. También es un número trascendente, lo que lo hace aún más especial en matemáticas.
Historia del Número e

A diferencia de 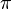 , el número e es más reciente en la historia de las matemáticas. Su origen está más relacionado con el análisis matemático que con la geometría.
, el número e es más reciente en la historia de las matemáticas. Su origen está más relacionado con el análisis matemático que con la geometría.
¿Quién lo descubrió y cómo se usó?
Las primeras menciones de esta constante aparecieron en 1618. Fue en un apéndice de un trabajo sobre logaritmos de John Napier. Sin embargo, esta tabla no mostraba el valor de la constante directamente. Se cree que la tabla fue escrita por William Oughtred.
Más tarde, en 1647, Saint-Vincent calculó el área bajo una curva especial llamada hipérbola. No está claro si vio la conexión con los logaritmos. Quien sí entendió esta relación fue Huygens en 1661. Él notó que el número e es el valor en el eje X para que el área bajo la curva 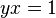 desde 1 sea igual a 1. Esta es la razón por la que e es la base de los logaritmos naturales.
desde 1 sea igual a 1. Esta es la razón por la que e es la base de los logaritmos naturales.
El problema del interés compuesto
El número e no se descubrió a través de los logaritmos, sino del estudio del interés compuesto. Este problema fue investigado por Jacob Bernoulli en 1683. Imagina que inviertes 1 unidad de dinero con un interés del 100% al año.
- Si te pagan el interés una vez al año, obtendrás 2 unidades.
- Si te pagan 2 veces al año (dividiendo el interés), obtendrás 1 x 1.502 = 2.25 unidades.
- Si te pagan 4 veces al año, obtendrás 1 x 1.254 = 2.4414 unidades.
- Si te pagan mensualmente, obtendrás 1 x
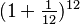 = 2.61303 unidades.
= 2.61303 unidades.
Bernoulli notó que, a medida que aumentas la cantidad de veces que se paga el interés en un año, la cantidad total se acerca a un límite. Este límite es el número e. Esta fue la primera vez que un número se definió como el resultado de un proceso de límite.
Gottfried Leibniz usó la letra 'b' para esta constante en 1690. Leonhard Euler empezó a usar la letra 'e' en 1727. Él publicó su uso en 1736 en su obra Mechanica. Euler hizo muchas contribuciones relacionadas con e. En 1748, en su libro Introductio in analysin infinitorum, dio una explicación completa de las ideas sobre e.
Propiedades y Usos del Número e
La Función Exponencial
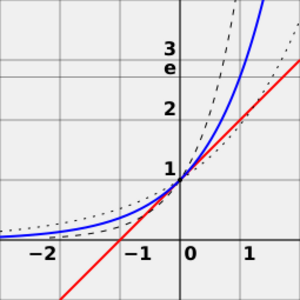
La función exponencial es una de las funciones más importantes en matemáticas. Se escribe como 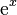 . Lo más interesante de esta función es que su derivada (su tasa de cambio) es igual a la función misma. Esto la hace muy útil en ecuaciones diferenciales, que describen cómo cambian las cosas.
. Lo más interesante de esta función es que su derivada (su tasa de cambio) es igual a la función misma. Esto la hace muy útil en ecuaciones diferenciales, que describen cómo cambian las cosas.
El Número e en la Probabilidad
El número e también aparece en la teoría de probabilidades. Un ejemplo es el "problema de los sombreros". Imagina que n invitados dejan sus sombreros. El mayordomo los devuelve al azar. La probabilidad de que ninguno reciba su propio sombrero se acerca a 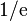 a medida que el número de invitados es muy grande.
a medida que el número de invitados es muy grande.
Otro ejemplo es el siguiente: si sumas números aleatorios entre 0 y 1, el número promedio de valores que necesitas sumar para que la suma sea mayor que 1 es e.
Además, e es fundamental en la distribución normal, que es una curva en forma de campana. Esta distribución es muy importante en estadística para entender datos y fenómenos naturales.
El Número e en la Geometría
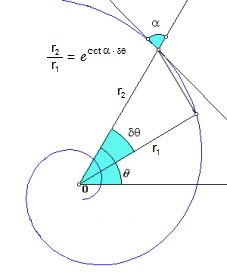
El número e también aparece en la geometría. Por ejemplo, en una espiral logarítmica (también llamada equiangular), si tomas dos puntos en la curva separados por un ángulo de 1 radián, la proporción de sus distancias al centro es e.
También se relaciona con la catenaria. Esta es la forma que toma una cuerda o cadena que cuelga libremente entre dos puntos, solo bajo la fuerza de la gravedad.
¿Es el número e un número especial?
Sí, el número  es irracional. Esto significa que no se puede escribir como una fracción de dos números enteros. Euler lo demostró en 1737.
es irracional. Esto significa que no se puede escribir como una fracción de dos números enteros. Euler lo demostró en 1737.
Además, es un número trascendente. Esto quiere decir que no es la solución de ninguna ecuación polinómica con coeficientes enteros. Fue el primer número trascendente que se demostró como tal. Charles Hermite lo probó en 1873.
¿Cómo se representa el número e?
El número  se puede representar de varias maneras en matemáticas:
se puede representar de varias maneras en matemáticas:
Como un límite
La forma más común de definir e es como el límite de una secuencia:
Esto significa que si haces n cada vez más grande, el valor de 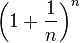 se acerca cada vez más a e.
se acerca cada vez más a e.
Como una suma infinita
También se puede expresar e como una suma infinita de fracciones:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \text{e}=\sum_{n=0}^\infty (n!)^{-1}
que se expande como
Donde n! significa el factorial de n (por ejemplo, 3! = 3x2x1 = 6).
Como una fracción continua
Aunque sus decimales no tienen un patrón, e tiene un patrón muy interesante cuando se escribe como una fracción continua:
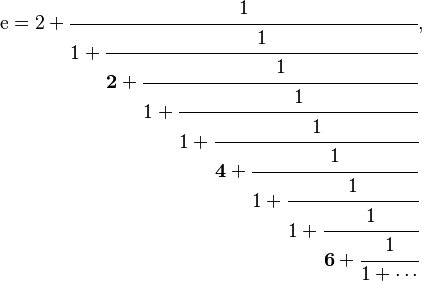
Este patrón fue descubierto por Leonhard Euler.
¿Cuántos dígitos de e conocemos?
El número de dígitos conocidos de e ha crecido mucho gracias a las computadoras. En 1949, John von Neumann y su equipo usaron la computadora ENIAC para calcular 2010 decimales. En 1961, Daniel Shanks y John Wrench calcularon más de 100,000 decimales. Para el año 2000, se habían calculado más de 12 mil millones de decimales. Hoy en día, se conocen billones de decimales de e.
| Fecha | Cantidad de cifras | Realizador del cálculo |
|---|---|---|
| 1690 | 1 | Jacob Bernoulli |
| 1714 | 13 | Roger Cotes |
| 1748 | 23 | Leonhard Euler |
| 1853 | 137 | William Shanks |
| 1871 | 205 | William Shanks |
| 1884 | 346 | J. Marcus Boorman |
| 1949 | 2,010 | John von Neumann (en el ENIAC) |
| 1961 | 100,265 | Daniel Shanks y John Wrench |
| 1978 | 116,000 | Steve Wozniak en el Apple II |
| 1994 | 10 000 000 | Robert Nemiroff y Jerry Bonnell |
| Mayo de 1997 | 18 199 978 | Patrick Demichel |
| Agosto de 1997 | 20 000 000 | Birger Seifert |
| Septiembre de 1997 | 50 000 817 | Patrick Demichel |
| Febrero de 1999 | 200 000 579 | Sebastián Wedeniwski |
| Octubre de 1999 | 869 894 101 | Sebastián Wedeniwski |
| 21 de noviembre de 1999 | 1 250 000 000 | Xavier Gourdon |
| 10 de julio de 2000 | 2 147 483 648 | Shigeru Kondo y Xavier Gourdon |
| 16 de julio de 2000 | 3 221 225 472 | Colin Martin y Xavier Gourdon |
| 2 de agosto de 2000 | 6 442 450 944 | Shigeru Kondo y Xavier Gourdon |
| 16 de agosto de 2000 | 12 884 901 000 | Shigeru Kondo y Xavier Gourdon |
| 21 de agosto de 2003 | 25 100 000 000 | Shigeru Kondo y Xavier Gourdon |
| 18 de septiembre de 2003 | 50 100 000 000 | Shigeru Kondo y Xavier Gourdon |
| 27 de abril de 2007 | 100 000 000 000 | Shigeru Kondo y Steve Pagliarulo |
| 6 de mayo de 2009 | 200 000 000 000 | Shigeru Kondo y Steve Pagliarulo |
| 21 de febrero de 2010 | 500 000 000 000 | Alexander J. Yee |
| 5 de julio de 2010 | 1 000 000 000 000 | Shigeru Kondo y Alexander J. Yee |
| 24 de junio de 2015 | 1 400 000 000 000 | Matthew Hebert |
| 5 de diciembre de 2020 | 31 415 926 535 897 | David Christle |
Las primeras cien cifras de  son:
son:
Curiosidades del Número e
A diferencia del número 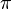 , el número e no es tan conocido por el público en general. Sin embargo, hay muchas personas que disfrutan memorizando sus dígitos. El récord actual de memorización es de 25,000 cifras.
, el número e no es tan conocido por el público en general. Sin embargo, hay muchas personas que disfrutan memorizando sus dígitos. El récord actual de memorización es de 25,000 cifras.
Galería de imágenes
-
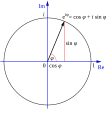
Representación geométrica de la fórmula de Euler
-
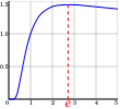
El máximo global de
![\sqrt[x]{x}](/images/math/8/6/b/86b78fe92eda77289ff8f1357b18924f.png) ocurre en
ocurre en  .
.
Véase también
 En inglés: E (mathematical constant) Facts for Kids
En inglés: E (mathematical constant) Facts for Kids



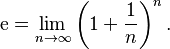
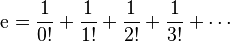
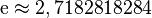
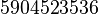
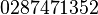
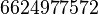
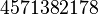
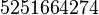

 y la gráfica Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = x^{-1} , entre
y la gráfica Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = x^{-1} , entre  y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = e es
y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = e es 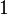 .
.