Problema de los puentes de Königsberg para niños
El problema de los puentes de Königsberg es un famoso problema matemático que fue resuelto por Leonhard Euler en el año 1736. La solución a este problema fue muy importante porque dio origen a una nueva rama de las matemáticas llamada la teoría de grafos.
El nombre del problema viene de la ciudad de Königsberg, que antes estaba en Prusia Oriental y Alemania, y que desde 1945 es la ciudad rusa de Kaliningrado.
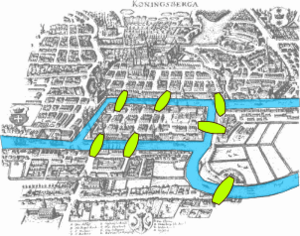
Esta ciudad está atravesada por el río Pregolia. El río se divide y rodea una isla llamada Kneiphof. Así, la ciudad quedaba dividida en cuatro zonas de tierra. Estas zonas estaban conectadas por siete puentes. El problema consistía en encontrar una forma de caminar por toda la ciudad, pasando por cada uno de los siete puentes una sola vez, y terminando en el mismo lugar donde se empezó.
Contenido
¿Quién fue Leonhard Euler y dónde surgió el problema?
Leonhard Euler fue un matemático muy importante que llegó a Prusia en 1741, cuando tenía 34 años. Vivió allí hasta 1766 y luego regresó a San Petersburgo. Durante esos años, trabajó en la Academia Prusiana de las Ciencias, donde hizo muchas investigaciones.
Königsberg era un lugar muy importante para la ciencia en esa época. Fue allí donde se planteó el problema de los puentes, que se hizo muy popular como un juego y un desafío matemático entre las personas inteligentes de ese tiempo.
¿Cómo ayudó este problema a las matemáticas?
La forma en que Euler pensó y resolvió este problema fue clave para crear la idea de un grafo. Un grafo es como un mapa simplificado donde los lugares se representan con puntos, llamados vértices, y las conexiones entre ellos se representan con líneas, llamadas aristas.
- Los vértices son los puntos o lugares.
- Las aristas son las líneas que conectan los vértices.
- El grado de un vértice es el número de aristas que llegan a él.
El diagrama que Euler hizo del mapa de Königsberg es un tipo de grafo especial.
En la teoría de grafos, existe un concepto llamado ciclo euleriano. Este nombre es un homenaje a Leonhard Euler. Un ciclo euleriano es un camino dentro de un grafo que recorre todas las aristas una sola vez y regresa al punto de partida.
La solución de Euler también fue el primer paso para entender los grafos planares. Estos son grafos que se pueden dibujar en una superficie plana sin que sus aristas se crucen.
Además, el trabajo de Euler fue el primero en hablar de una nueva forma de ver la geometría. En lugar de solo medir las cosas, esta nueva geometría se interesa por cómo están conectadas las partes de un objeto. Euler la llamó "geometriam situs", que hoy conocemos como topología. La topología es una rama de las matemáticas que estudia las propiedades de los objetos que no cambian cuando se estiran o se doblan.
¿Cómo están los puentes hoy en día?

Con el paso del tiempo, algunos de los siete puentes originales de Königsberg fueron dañados o reemplazados. Dos de ellos fueron destruidos y otros dos fueron demolidos para construir carreteras modernas. De los tres puentes que quedan, solo dos son los originales de la época de Euler, ya que uno fue reconstruido en 1935.
Actualmente, en Kaliningrado solo hay cinco puentes. Con esta nueva distribución, ahora sí es posible encontrar un camino euleriano. Esto significa que se puede recorrer todos los puentes una sola vez, pero la ruta empieza en una zona y termina en otra diferente. Sin embargo, todavía no es posible hacer un ciclo euleriano, es decir, empezar y terminar en el mismo lugar, que era la condición original del problema.
Véase también
 En inglés: Seven Bridges of Königsberg Facts for Kids
En inglés: Seven Bridges of Königsberg Facts for Kids
- Ciclo euleriano
- Teoría de grafos

