Función trigonométrica para niños
Datos para niños Trigonometría |
||
|---|---|---|
 |
||
| Referencias | ||
| Constantes exactas ·Tablas ·Circunferencia goniométrica |
||
| Funciones, leyes y teoremas | ||
| Funciones e (inversas) ·Senos ·Cosenos ·Tangentes ·Cotangentes ·Teorema de Pitágoras·Identidades y fórmulas de trigonometría |
||
| Cálculo infinitesimal | ||
| Sustitución trigonométrica ·Integrales de funciones directas (e inversas) ·Derivadas | ||
| Temas relacionados | ||
| Temas ·Historia ·Usos·Trigonometría generalizada |
En matemáticas, las funciones trigonométricas son herramientas especiales que nos ayudan a entender y calcular cosas relacionadas con los ángulos y los triángulos. Son como las "reglas" que nos dicen cómo se relacionan los lados de un triángulo con sus ángulos. Las más conocidas son el seno, coseno y tangente, pero también existen la cotangente, secante y cosecante.
Estas funciones son muy importantes y se usan en muchos campos, como la física (para estudiar ondas o movimientos), la astronomía (para calcular posiciones de estrellas), la cartografía (para hacer mapas), la náutica (para navegar barcos), las telecomunicaciones (para enviar señales) y para describir fenómenos que se repiten, como las mareas o las ondas de sonido.
Contenido
¿Qué son las funciones trigonométricas?
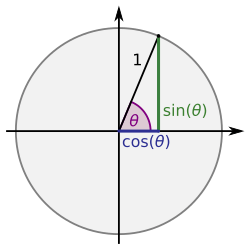
Las funciones trigonométricas se pueden entender de varias maneras. Una forma sencilla es verlas como la relación entre los lados de un triángulo rectángulo y uno de sus ángulos. Imagina un triángulo con un ángulo de 90 grados. Si conoces un ángulo y un lado, estas funciones te ayudan a encontrar los otros lados y ángulos.
También se pueden definir usando una circunferencia unitaria, que es un círculo con un radio de 1. Esto permite que las funciones se usen con cualquier ángulo, no solo los de un triángulo rectángulo.
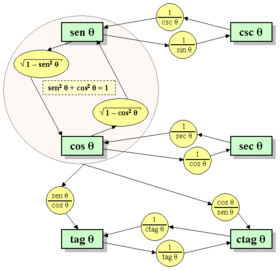
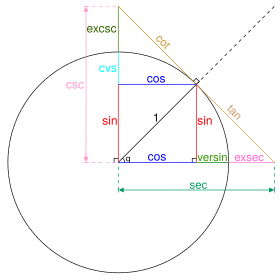
Existen seis funciones trigonométricas principales. Las últimas cuatro (cotangente, secante y cosecante) se pueden calcular a partir de las dos primeras (seno y coseno).
| Función | Abreviatura | Cómo se relaciona |
|---|---|---|
| Seno | sen, sin | Es la inversa de la cosecante. |
| Coseno | cos | Es la inversa de la secante. |
| Tangente | tan, tg | Es la inversa de la cotangente. También es seno dividido por coseno. |
| Cotangente | ctg (cot) | Es la inversa de la tangente. También es coseno dividido por seno. |
| Secante | sec | Es la inversa del coseno. |
| Cosecante | csc (cosec) | Es la inversa del seno. |
¿Cómo se definen en un triángulo rectángulo?
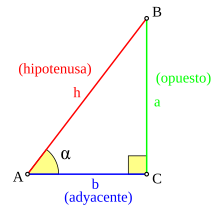
Para entender mejor estas funciones, vamos a usar un triángulo rectángulo. Este triángulo tiene un ángulo de 90 grados. Los lados de este triángulo tienen nombres especiales:
- La hipotenusa (h) es el lado más largo y siempre está enfrente del ángulo de 90 grados.
- El cateto opuesto (a) es el lado que está enfrente del ángulo que estamos estudiando (llamémoslo
 ).
). - El cateto adyacente (b) es el lado que está al lado del ángulo
 (pero no es la hipotenusa).
(pero no es la hipotenusa).
En cualquier triángulo rectángulo, los otros dos ángulos (los que no son de 90 grados) siempre están entre 0 y 90 grados. Las definiciones de las funciones trigonométricas para estos ángulos son:
1) El seno de un ángulo es la división de la longitud del cateto opuesto entre la longitud de la hipotenusa:

Lo interesante es que esta relación siempre es la misma para un ángulo dado, sin importar el tamaño del triángulo.
2) El coseno de un ángulo es la división de la longitud del cateto adyacente entre la longitud de la hipotenusa:

3) La tangente de un ángulo es la división de la longitud del cateto opuesto entre la del cateto adyacente:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname {tg} \alpha = \frac {{ \color{ForestGreen}\textrm{opuesto}}} {{ \color{Blue}\textrm{adyacente}}} = \frac {a} {b}
4) La cotangente de un ángulo es la división de la longitud del cateto adyacente entre la del cateto opuesto:
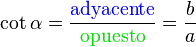
5) La secante de un ángulo es la división de la longitud de la hipotenusa entre la longitud del cateto adyacente:

6) La cosecante de un ángulo es la división de la longitud de la hipotenusa entre la longitud del cateto opuesto:

Valores de funciones para ángulos especiales
Hay algunos ángulos que son muy comunes en trigonometría y es útil conocer los valores de sus funciones. La siguiente tabla muestra algunos de estos valores. El símbolo ∞ significa que el valor es muy, muy grande (tiende a infinito).
| Radianes | Grado | Seno | Coseno | Tangente | Cotangente | Secante | Cosecante |
|---|---|---|---|---|---|---|---|
| 0 | 0° | 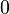 |
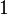 |
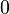 |
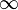 |
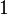 |
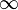 |
| π/12 | 15° | 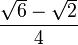 |
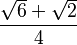 |
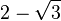 |
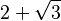 |
 |
 |
| π/10 | 18° | 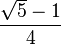 |
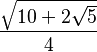 |
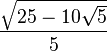 |
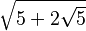 |
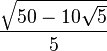 |
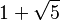 |
| π/8 | 22.5° | 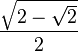 |
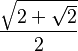 |
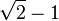 |
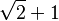 |
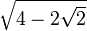 |
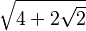 |
| π/6 | 30° |  |
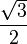 |
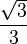 |
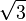 |
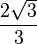 |
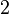 |
| π/5 | 36° | 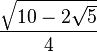 |
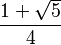 |
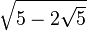 |
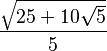 |
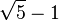 |
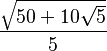 |
| π/4 | 45° | 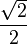 |
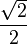 |
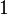 |
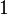 |
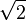 |
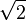 |
| 3π/10 | 54° | 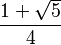 |
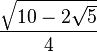 |
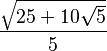 |
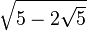 |
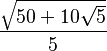 |
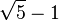 |
| π/3 | 60° | 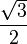 |
 |
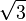 |
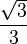 |
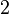 |
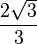 |
| 3π/8 | 67.5° | 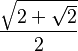 |
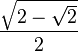 |
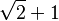 |
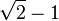 |
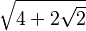 |
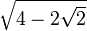 |
| 2π/5 | 72° | 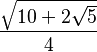 |
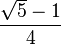 |
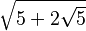 |
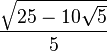 |
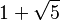 |
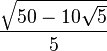 |
| 5π/12 | 75° | 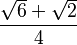 |
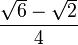 |
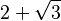 |
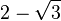 |
 |
 |
| π/2 | 90° | 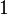 |
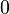 |
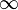 |
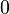 |
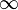 |
 |
¿Cómo se definen para cualquier número?
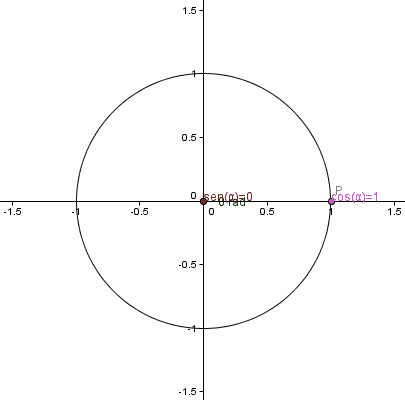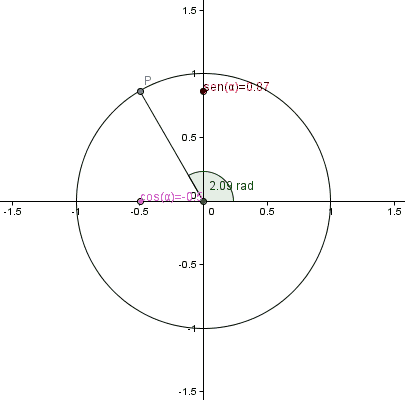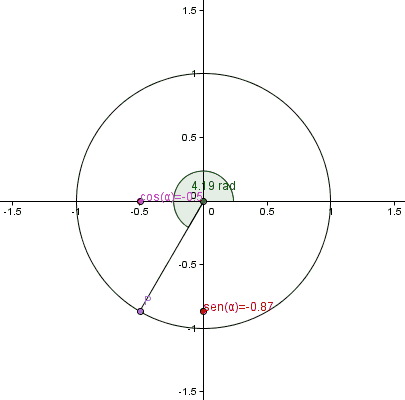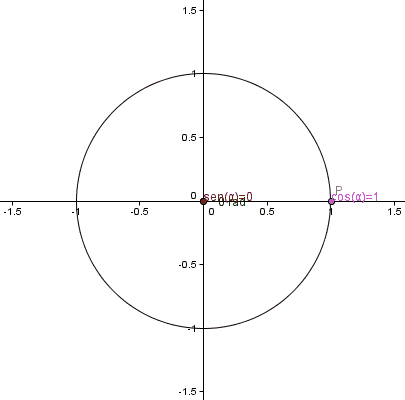
Para usar las funciones trigonométricas con ángulos mayores de 90 grados o incluso negativos, usamos una circunferencia unitaria (un círculo con radio 1) en un plano cartesiano.
Imagina un punto P en este círculo. Las coordenadas de este punto (x, y) nos dan el coseno (x) y el seno (y) del ángulo. Este ángulo se mide desde el eje positivo X hasta la línea que une el centro del círculo con el punto P.
Con esta definición, los valores del seno y coseno siempre estarán entre -1 y 1. Si el ángulo es mayor de 360 grados (o 2π radianes), simplemente damos una vuelta completa al círculo y volvemos a la misma posición, por lo que los valores de las funciones se repiten.
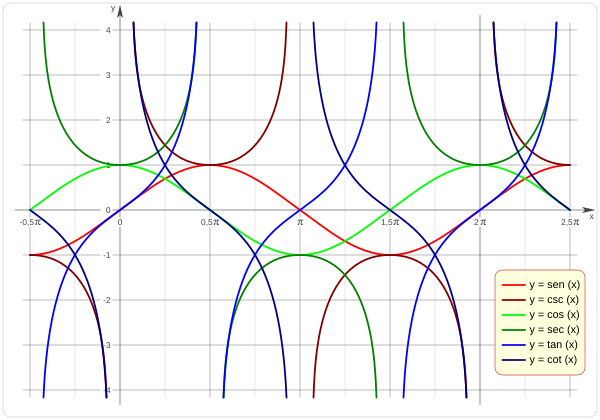
¿Cómo se ven las funciones trigonométricas?
Las funciones trigonométricas tienen formas muy interesantes cuando las dibujamos en una gráfica. Se repiten una y otra vez, como las ondas. Por eso son tan útiles para describir fenómenos que son periódicos, es decir, que se repiten con el tiempo.
Funciones trigonométricas inversas
Así como podemos calcular el seno de un ángulo, también podemos hacer lo contrario: encontrar el ángulo si conocemos su seno. Para esto, usamos las funciones trigonométricas inversas. Las más comunes son:
- Arcoseno: Es la función inversa del seno. Si sabes el valor del seno, el arcoseno te dice cuál es el ángulo. Se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname{arcsen}(x) .
- Arcocoseno: Es la función inversa del coseno. Si sabes el valor del coseno, el arcocoseno te dice cuál es el ángulo. Se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \arccos (x) .
- Arcotangente: Es la función inversa de la tangente. Si sabes el valor de la tangente, la arcotangente te dice cuál es el ángulo. Se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname {arctg} (x) .
Historia de las funciones trigonométricas
El estudio de las funciones trigonométricas es muy antiguo. Se remonta a la época de Babilonia, hace miles de años. Muchos de los conceptos básicos de la trigonometría fueron desarrollados por matemáticos de la Antigua Grecia, de la India y por estudiosos musulmanes.
El primer uso de la función seno se encuentra en textos de la India de los siglos VIII al VI a.C. Matemáticos importantes como Hiparco de Nicea, Aryabhata y Muhammad ibn Musa al-Khwarizmi contribuyeron a su desarrollo.
En Europa, fue Leonhard Euler quien, en 1748, estableció la forma moderna de entender las funciones trigonométricas, definiéndolas con series infinitas.
La idea principal detrás de estas funciones es que en triángulos que son "similares" (es decir, que tienen los mismos ángulos, aunque sean de diferente tamaño), las proporciones entre sus lados siempre son las mismas. Las funciones trigonométricas son precisamente esas proporciones.
Véase también
 En inglés: Trigonometric functions Facts for Kids
En inglés: Trigonometric functions Facts for Kids
- Trigonometría
- Identidad trigonométrica
- Seno, coseno, tangente
- Hexágono trigonométrico. Una herramienta para recordar relaciones trigonométricas.
|