Constante de Euler-Mascheroni para niños
La Constante de Euler-Mascheroni es un número especial en matemáticas, como el famoso número Pi (π). Se le representa con la letra griega minúscula gamma (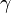
). Este número aparece mucho en una rama de las matemáticas llamada teoría de números.
Se define como el resultado de una operación matemática llamada "límite". Imagina que tienes una lista de fracciones que se suman (llamada serie armónica) y, al mismo tiempo, calculas el logaritmo natural de un número. La constante de Euler-Mascheroni es la diferencia entre estas dos cosas cuando se hacen muy, muy grandes.
Su valor aproximado es: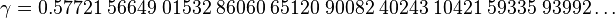 
Es importante no confundirla con el número e, que a veces también se llama "número de Euler".
Contenido
Su Historia: Euler y Mascheroni
La constante de Euler-Mascheroni fue descubierta por primera vez en 1734. El matemático suizo Leonhard Euler la mencionó en un escrito llamado De Progressionibus harmonicis observationes. En ese momento, Euler calculó los primeros 6 dígitos de la constante y la llamó "C". Más tarde, en 1781, logró calcular 10 decimales más.
En 1790, otro matemático, Lorenzo Mascheroni, calculó aún más decimales, llegando a los primeros 19. Él la llamó "A". Con el tiempo, se empezó a usar la letra griega 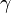para representarla, debido a su conexión con otra función matemática importante, la función gamma.
¿Es Racional o Irracional? Un Misterio Matemático
Una de las preguntas más interesantes sobre la constante 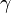es si es un número irracional o no. Un número irracional es aquel que no se puede escribir como una fracción simple (como 1/2 o 3/4). Por ejemplo, Pi (π) es un número irracional.
Hasta ahora, los matemáticos no han podido demostrar si 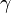es racional o irracional. ¡Es uno de los grandes misterios sin resolver en el mundo de las matemáticas! Si fuera un número racional, su denominador (la parte de abajo de la fracción) tendría que ser un número gigantesco, ¡mucho más grande que cualquier cosa que podamos imaginar fácilmente!
¿Dónde Aparece esta Constante?
La constante de Euler-Mascheroni aparece en muchos lugares diferentes de las matemáticas, especialmente en la teoría de números. Aquí te mencionamos algunos ejemplos de dónde se puede encontrar:
- En fórmulas que usan la función integral exponencial.
- Cuando se calcula la transformada de Laplace del logaritmo natural.
- Es el primer término de una serie especial de la función zeta de Riemann.
- Está relacionada con la Función digamma.
- Aparece en la fórmula del producto de Weierstrass para la función gamma.
- En cálculos relacionados con la Función φ de Euler.
- En la proporción de crecimiento de la función divisor.
- En el cálculo de la constante Meissel-Mertens.
- En el tercero de los Teoremas de Mertens.
Véase también
En inglés: Euler's constant Facts for Kids
