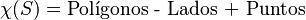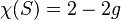Característica de Euler para niños
La característica de Euler es un número especial que nos ayuda a entender la forma de los objetos, especialmente en matemáticas. Imagina que puedes estirar, doblar o aplastar una figura sin romperla ni pegarla. La característica de Euler de esa figura no cambiará, por eso se le llama un invariante topológico. Se representa con la letra griega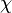 
(se pronuncia "ji").
Este concepto fue usado por primera vez para estudiar los poliedros, que son figuras 3D con caras planas, como los cubos o las pirámides. El matemático Leonhard Euler fue quien lo popularizó, y por eso lleva su nombre.
La fórmula más conocida para calcular la característica de Euler de un poliedro es muy sencilla:
|
Donde:
- Vértices son las esquinas del poliedro.
- Aristas son las líneas que conectan los vértices.
- Caras son las superficies planas del poliedro.
Contenido
Característica de Euler en Poliedros
Para cualquier poliedro que se parezca a una esfera (es decir, que se pueda transformar en una esfera sin romperse), la característica de Euler siempre será 2.
Por ejemplo:
- Un cubo tiene 8 vértices, 12 aristas y 6 caras. Si aplicamos la fórmula: 8 - 12 + 6 = 2.
- Un tetraedro (una pirámide de base triangular) tiene 4 vértices, 6 aristas y 4 caras. Si aplicamos la fórmula: 4 - 6 + 4 = 2.
Aquí tienes una tabla con más ejemplos de poliedros y su característica de Euler:
| Nombre | Imagen | Vértices V |
Aristas A |
Caras C |
Característica de Euler: V − A + C |
|---|---|---|---|---|---|
| Tetraedro |  |
4 | 6 | 4 | 2 |
| Cubo |  |
8 | 12 | 6 | 2 |
| Octaedro |  |
6 | 12 | 8 | 2 |
| Dodecaedro |  |
20 | 30 | 12 | 2 |
| Icosaedro |  |
12 | 30 | 20 | 2 |
Pero no todos los poliedros tienen una característica de Euler de 2. Por ejemplo, un poliedro toroidal (que tiene forma de rosquilla o dona) puede tener una característica de Euler diferente. El poliedro toroidal de la imagen tiene 22 vértices, 70 aristas y 48 caras. Si aplicamos la fórmula: 22 - 70 + 48 = 0.
Aquí hay otros ejemplos de poliedros con diferentes características de Euler:
| Nombre | Imagen | Vértices V |
Aristas A |
Caras C |
Característica de Euler : V − A + C |
|---|---|---|---|---|---|
| Tetrahemihexaedro |  |
6 | 12 | 7 | 1 |
| Octahemioctaedro |  |
12 | 24 | 12 | 0 |
| Cubohemioctaedro |  |
12 | 24 | 10 | −2 |
| Gran Icosaedro |  |
12 | 30 | 20 | 2 |
Característica de Euler en Grafos Planos
La característica de Euler también se puede usar para grafo planos, que son dibujos de puntos (vértices) y líneas (aristas) en una superficie plana, sin que las líneas se crucen. En este caso, la fórmula es la misma: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V - E + F , donde F es el número de "caras" o regiones que el grafo divide en el plano, incluyendo la región exterior.
Para cualquier grafo plano que esté conectado (es decir, que no esté dividido en partes separadas), la característica de Euler siempre es 2.
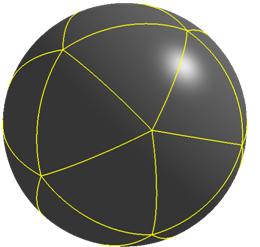
Generalización a las Superficies
Podemos extender la idea de la característica de Euler a superficies que no son poliedros, como una esfera o un toro (una rosquilla). Para hacer esto, imaginamos que la superficie está cubierta por una especie de "malla" de polígonos (como triángulos o cuadrados).
La fórmula para la característica de Euler de una superficie S es:
Donde:
- Polígonos son las caras de la malla.
- Lados son las aristas de la malla.
- Puntos son los vértices de la malla.
La característica de Euler de una superficie cerrada (sin bordes) también se relaciona con su género (g). El género es un número que nos dice cuántos "agujeros" o "asas" tiene la superficie.
La relación es:
Por ejemplo:
- Una esfera no tiene agujeros, así que su género es 0. Su característica de Euler es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2 - 2 \times 0 = 2 .
- Un toro (una rosquilla) tiene un agujero, así que su género es 1. Su característica de Euler es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2 - 2 \times 1 = 0 .
- Un doble toro (como dos rosquillas pegadas) tiene dos agujeros, así que su género es 2. Su característica de Euler es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2 - 2 \times 2 = -2 .
Aquí tienes una tabla con la característica de Euler de algunas formas:
| Nombre | Imagen | Característica de Euler |
|---|---|---|
| Segmento |  |
1 |
| Circunferencia |  |
0 |
| Disco |  |
1 |
| Esfera |  |
2 |
| Тоro (producto de dos círculos) |
 |
0 |
| Doble toro |  |
−2 |
| Тriple toro |  |
−4 |
| Plano proyectivo real |
 |
1 |
| Banda de Möbius |  |
0 |
| Botella de Klein |  |
0 |
| Dos esferas (desconectadas) | |
2 + 2 = 4 |
| Tres esferas (desconectadas) | |
2 + 2 + 2 = 6 |
Propiedades Importantes
La característica de Euler tiene algunas propiedades interesantes:
- No cambia al deformar: Si dos formas se pueden transformar una en la otra sin romperse ni pegarse (se dice que son "homotópicamente equivalentes"), tendrán la misma característica de Euler. Por ejemplo, una bola sólida y un punto tienen característica de Euler 1.
- Unión de formas: Si unes dos formas separadas, la característica de Euler de la unión es la suma de las características de Euler de cada forma. Por ejemplo, si tienes dos esferas separadas, su característica de Euler combinada es 2 + 2 = 4.
Galería de imágenes
-
Primeros pasos de la prueba en el caso de un cubo
Véase también
En inglés: Euler characteristic Facts for Kids
