Logaritmo natural para niños
Datos para niños Logaritmo Natural |
||
|---|---|---|
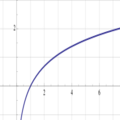
 Gráfica de Logaritmo Natural
|
||
| Definición | 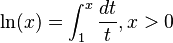 |
|
| Tipo | Función real | |
| Descubridor(es) | John Napier (1614) | |
| Dominio | 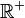 |
|
| Codominio | 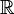 |
|
| Imagen | 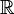 |
|
| Propiedades | Biyectiva Cóncava Estrictamente creciente Continua Trascendente |
|
| Cálculo infinitesimal | ||
| Derivada |  |
|
| Función inversa | 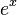 |
|
| Límites | 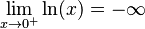 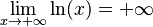 |
|
| Funciones relacionadas | Logaritmo Función exponencial |
|
En matemáticas, el Logaritmo Natural es un tipo especial de logaritmo. Su base es un número muy importante llamado e. Este número e es irracional, lo que significa que tiene infinitos decimales que no se repiten. Su valor aproximado es 2.718281828459.
El logaritmo natural de un número x se escribe como 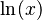 o a veces como
o a veces como 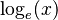 . Nos dice a qué potencia debemos elevar el número e para obtener x. Por ejemplo, si
. Nos dice a qué potencia debemos elevar el número e para obtener x. Por ejemplo, si 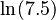 es aproximadamente 2.0149, significa que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{2.0149\dots} es igual a 7.5.
es aproximadamente 2.0149, significa que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{2.0149\dots} es igual a 7.5.
El logaritmo natural de e es 1, porque  . El logaritmo natural de 1 es 0, porque
. El logaritmo natural de 1 es 0, porque  .
.
El logaritmo natural es la función inversa de la función exponencial natural. Esto significa que si aplicas una y luego la otra, vuelves al número original.
Contenido
Logaritmo Natural: ¿Qué es y para qué sirve?
El logaritmo natural es una herramienta matemática fundamental. Se usa en muchas áreas, desde la física y la ingeniería hasta la economía. Nos ayuda a entender cómo crecen o disminuyen las cosas de forma continua.
¿Qué es el número 'e'?
El número e es una constante matemática muy especial. Aparece de forma natural en problemas de crecimiento y cambio. Por ejemplo, si algo crece a una tasa constante, el número e nos ayuda a calcular su valor en el futuro. Es tan importante como el número π en la geometría.
¿Por qué se llama "natural"?
Podría parecer que el logaritmo con base 10 (el que usamos en la vida diaria) sería más "natural". Sin embargo, el logaritmo natural (con base e) es el que aparece más a menudo en las fórmulas matemáticas.
Por ejemplo, cuando se estudia el cálculo, la derivada del logaritmo natural es muy sencilla: 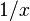 . Esto no ocurre con logaritmos de otras bases. Esta simplicidad es una de las razones por las que se le considera "natural".
. Esto no ocurre con logaritmos de otras bases. Esta simplicidad es una de las razones por las que se le considera "natural".
¿Cómo se define el Logaritmo Natural?
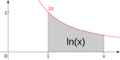
El logaritmo natural de un número x (siempre que x sea mayor que 0) se puede entender como el área bajo una curva especial. Imagina la gráfica de la función 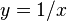 . El logaritmo natural de x es el área que hay debajo de esta curva, desde el punto donde x es 1 hasta el valor de x que te interesa.
. El logaritmo natural de x es el área que hay debajo de esta curva, desde el punto donde x es 1 hasta el valor de x que te interesa.
Propiedades importantes
El logaritmo natural tiene propiedades que facilitan los cálculos. Aquí te mostramos algunas:
- Multiplicación: El logaritmo natural de un producto es la suma de los logaritmos naturales:
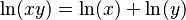 .
. - Potencias: El logaritmo natural de un número elevado a una potencia es la potencia multiplicada por el logaritmo natural del número:
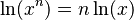 .
. - División: El logaritmo natural de una división es la resta de los logaritmos naturales:
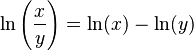 .
. - Logaritmo de 1: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ln(1) = 0 .
- Logaritmo de e:
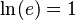 .
.
La derivada del Logaritmo Natural
En cálculo, la derivada nos dice cómo cambia una función. La derivada del logaritmo natural de x es muy simple:  . Esto significa que la tasa de cambio del logaritmo natural es inversamente proporcional a x.
. Esto significa que la tasa de cambio del logaritmo natural es inversamente proporcional a x.
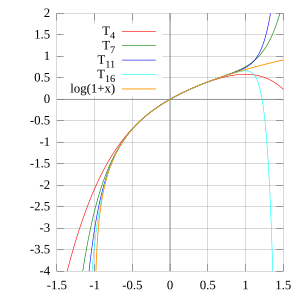
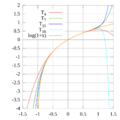
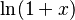 son aproximaciones. Para
son aproximaciones. Para 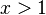 , las aproximaciones pueden no ser muy precisas.
, las aproximaciones pueden no ser muy precisas.Series y aproximaciones
El logaritmo natural también se puede expresar como una serie matemática, que es una suma infinita de términos. Esto es útil para calcular su valor de forma aproximada. Una de las series más conocidas para 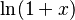 es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ln(1+x) = x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots Esta serie funciona bien para valores de x cercanos a cero.
es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ln(1+x) = x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots Esta serie funciona bien para valores de x cercanos a cero.
Usos del Logaritmo Natural
El logaritmo natural es una herramienta poderosa en matemáticas y ciencias.
Integración con Logaritmo Natural
En cálculo, la integración es el proceso inverso de la derivada. El logaritmo natural es muy útil para integrar ciertas funciones. Por ejemplo, la integral de 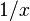 es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ln|x| más una constante.
es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ln|x| más una constante.
Esto significa que si tienes una función que es la derivada de otra dividida por esa misma función, su integral será el logaritmo natural del valor absoluto de la función original.
Cálculo de valores numéricos
Antes de las calculadoras, las personas usaban tablas y propiedades de los logaritmos para calcular sus valores. Por ejemplo, para calcular Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ln(7890.12345) , se podía reescribir como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ln(7.89012345 \cdot 10^3) . Usando las propiedades, esto se convierte en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ln(7.89012345) + 3 \ln(10) . Así, solo necesitabas el logaritmo de un número más pequeño y el logaritmo de 10.
El logaritmo natural de 10 es aproximadamente 2.30258509. Es un valor muy importante para trabajar con números grandes o pequeños, especialmente los que se escriben en notación científica.
Historia del Logaritmo Natural
La primera vez que se mencionó algo parecido al logaritmo natural fue en 1668, en un trabajo de Nikolaus Mercator llamado Logarithmotechnia. Sin embargo, el profesor de matemáticas John Speidell ya había creado tablas de valores de logaritmos naturales en 1619.
Al principio, se le llamó logaritmo hiperbólico. Esto se debe a que sus valores estaban relacionados con el área bajo una hipérbola. A veces también se le conoce como logaritmo neperiano, aunque este término tiene un significado un poco diferente al original.
Véase también
Galería de imágenes
de:Logarithmus#Natürlicher Logarithmus


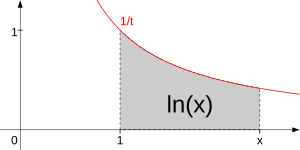
 entre
entre  y
y  . Si
. Si  , el área se considera negativa.
, el área se considera negativa.