Joseph-Louis Lagrange para niños
Datos para niños Joseph-Louis Lagrange |
||
|---|---|---|
 |
||
| Información personal | ||
| Nombre de nacimiento | Giuseppe Ludovico Lagrangia | |
| Nacimiento | 25 de enero de 1736 Turín (Reino de Cerdeña) |
|
| Fallecimiento | 10 de abril de 1813 París (Primer Imperio francés) |
|
| Sepultura | Panteón de París | |
| Nacionalidad | Francesa (desde 1802) | |
| Lengua materna | Italiano | |
| Familia | ||
| Cónyuge |
|
|
| Educación | ||
| Educado en | Universidad de Turín (hasta 1754) | |
| Supervisor doctoral | Giovanni Battista Beccaria | |
| Alumno de |
|
|
| Información profesional | ||
| Ocupación | Matemático, astrónomo, físico, político, escritor y profesor universitario | |
| Área | Análisis matemático, teoría de números, Analytical mechanics, mecánica celeste, cálculo infinitesimal, matemáticas y astronomía | |
| Cargos ocupados |
|
|
| Empleador |
|
|
| Estudiantes doctorales | Siméon Denis Poisson, Giovanni Plana y Jean-Baptiste Joseph Fourier | |
| Miembro de |
|
|
| Distinciones |
|
|
| Firma | ||
Joseph-Louis Lagrange (nacido como Giuseppe Ludovico Lagrangia), también conocido como Lagrange, fue un brillante físico, matemático y astrónomo. Nació en Turín el 25 de enero de 1736 y falleció en París el 10 de abril de 1813. Aunque nació en Italia, pasó gran parte de su vida trabajando en Prusia y Francia.
Lagrange trabajó en Berlín durante veinte años para el rey Federico II de Prusia. Hizo descubrimientos muy importantes en muchas áreas de las matemáticas. También desarrolló la mecánica Lagrangiana, una forma de entender cómo se mueven los objetos, y realizó trabajos innovadores en astronomía. Por la importancia y cantidad de sus aportaciones, es considerado uno de los científicos más destacados de la historia.
Contenido
La vida de Joseph-Louis Lagrange
Sus primeros años y el inicio de su pasión

Joseph-Louis Lagrange venía de una familia de buena posición social en París. Fue el mayor de once hermanos, pero el único que llegó a ser adulto.
Estudió en la Universidad de Turín. No fue hasta los diecisiete años cuando se interesó por las matemáticas. Su pasión comenzó al leer un ensayo del astrónomo Edmund Halley sobre análisis matemático (una rama de las matemáticas que estudia el cambio y el movimiento). Después de un año de mucho estudio, ya era un matemático muy hábil.
En 1755, el rey Carlos Manuel III de Cerdeña le pidió que enseñara a los artilleros de su ejército. Allí aplicó nuevas ideas sobre cómo se mueven los proyectiles. Sin embargo, Lagrange prefería la teoría abstracta a la práctica, lo que a veces lo hacía un profesor difícil para algunos.
Cuando tenía solo diecinueve años, Lagrange le envió una carta al famoso matemático Leonhard Euler. En ella, le proponía una nueva forma de resolver problemas de cálculo de variaciones (una rama de las matemáticas que busca la mejor forma de hacer algo). Euler reconoció que el método de Lagrange era muy bueno y le dio tiempo para que terminara su trabajo antes de publicar el suyo. Este descubrimiento hizo que Lagrange fuera reconocido como uno de los matemáticos más importantes de su tiempo.
En 1758, Lagrange y sus alumnos publicaron sus primeros trabajos en la Academia de Turín. Estos escritos se conocen como Miscellanea Taurinensia.
En 1761, Lagrange era el mejor en matemáticas. Pero trabajar tanto durante nueve años afectó su salud. Los médicos le dijeron que debía descansar. Aunque se recuperó un poco, su sistema nervioso nunca volvió a ser el mismo y sufrió de melancolía.
Lagrange era de estatura media, delgado, con ojos azules claros y piel pálida. Era nervioso y tímido, y no le gustaban las discusiones. Prefería dejar que otros se llevaran el crédito por sus ideas para evitar problemas.
En la corte de Prusia
En 1756, Euler intentó que Lagrange fuera a la academia de Berlín. Más tarde, d'Alembert convenció a Federico de Prusia para que invitara a Lagrange a Berlín, ofreciéndole un puesto muy importante.
En 1766, Euler se fue de Berlín. Federico II le escribió a Lagrange diciendo que el "rey más grande de Europa" debía tener al "matemático más grande de Europa" en su corte. Lagrange aceptó y pasó veinte años en Prusia. Durante este tiempo, publicó muchísimos trabajos científicos, incluyendo su obra más importante, la Mécanique analytique. Lagrange reemplazó a Euler como director de la Academia de las Ciencias de Berlín.
Su tiempo en Berlín empezó con un matrimonio que no fue feliz, y su esposa falleció pronto.
Lagrange era el favorito del rey. Le gustaba hablar sobre la importancia de la regularidad en la vida. Él mismo aplicaba esto: estudiaba su mente y cuerpo como si fueran máquinas para saber cuánto podía trabajar sin enfermarse. Cada noche se fijaba una tarea para el día siguiente y, al terminar un tema, lo revisaba para mejorarlo. Pensaba mucho antes de escribir y sus textos solían ser perfectos desde la primera vez.
Su etapa en Francia
En 1786, Federico II murió. Lagrange, que ya se había acostumbrado a Berlín, aceptó la invitación de Luis XVI para ir a París. También había recibido invitaciones de España y Nápoles. En Francia, fue recibido con honores y le dieron apartamentos especiales en el Louvre.
Al principio, sufrió de melancolía y no abrió una copia de su libro Mécanique durante más de dos años. La curiosidad por la Revolución francesa lo sacó de su tristeza, aunque pronto se preocupó por cómo se desarrollaba la revolución.
En 1792, una joven se compadeció de su tristeza y timidez y se casó con él, lo que lo hizo muy feliz. Aunque no tuvo que irse de Francia como otros extranjeros, quiso hacerlo cuando le ofrecieron presidir la comisión para reformar los pesos y medidas. Gracias a él, se adoptó el sistema decimal en 1799.
Aunque Lagrange quiso irse de Francia, nunca estuvo en peligro. Los gobiernos revolucionarios y luego Napoleón Bonaparte le dieron muchos honores. En 1794, Lagrange fue profesor en la École Polytechnique. Sus clases se basaban en su libro Théorie des fonctions analytiques.
Sin embargo, no fue un maestro perfecto. Fourier, uno de sus alumnos, escribió que su voz era débil, tenía acento italiano y que los estudiantes no lo apreciaban mucho, aunque los profesores sí.
En 1795, Lagrange tuvo una cátedra honorífica en la École Normale, pero solo por cuatro meses, ya que la escuela cerró. Sus clases allí eran básicas. Ese mismo año, fue uno de los diez miembros fundadores del Bureau des Longitudes, una oficina para mejorar la navegación.
Sus últimos años
En 1810, Lagrange empezó a revisar su Mécanique analytique, pero solo pudo completar dos tercios antes de morir en 1813 en París. Napoleón Bonaparte le dio la Gran Cruz de la Orden Imperial de la Reunión dos días antes de su muerte. Fue enterrado en el Panteón de París. En su tumba se lee:
|
JOSEPH LOUIS LAGRANGE. Senador. Conde del Imperio. Gran Oficial de la Legión de Honor. Gran Cruz de la Imperial Orden de la Reunión. Miembro del Instituto y la Oficina de Longitudes. Nacido en Turín el 25 de enero de 1736. Muerto en París el 10 de abril de 1813. |
Sus grandes aportaciones científicas
Lagrange fue un genio que hizo contribuciones importantes en muchas áreas de las matemáticas y la física.
Primeros trabajos y publicaciones
En 1758, Lagrange fundó una sociedad que luego se convirtió en la Academia Turinesa de Ciencias. Sus primeros trabajos se publicaron en los cinco volúmenes de los registros de esta Academia, conocidos como Miscellanea Taurinensia.
- El primer volumen incluye un estudio sobre cómo se propaga el sonido. En él, corrigió un error de Newton y encontró una ecuación general para el movimiento. También resolvió el problema de una cuerda que vibra.
- El segundo volumen contiene un trabajo extenso sobre el cálculo de variaciones y cómo se aplica a la dinámica (el estudio del movimiento y las fuerzas).
- El tercer volumen incluye soluciones a problemas de dinámica y cálculo integral. También abordó el Problema de los N-cuerpos (cómo se mueven varios cuerpos que se atraen entre sí) y el Problema de los tres cuerpos (un caso especial con solo tres cuerpos).
Trabajos importantes en Prusia
Durante sus veinte años en Prusia, Lagrange fue increíblemente productivo. No solo escribió su famosa Mécanique analytique, sino que también publicó unos doscientos trabajos en las Academias de Berlín, Turín y París. Muchos de estos eran como libros pequeños y todos eran de una calidad excepcional.
- En 1771, publicó un trabajo importante sobre cómo combinar observaciones astronómicas para obtener el resultado más preciso.
- También escribió sobre la presión de los fluidos en movimiento y sobre la integración de series infinitas.
Descubrimientos en astronomía
Lagrange hizo muchos descubrimientos en astronomía.
- En 1764, explicó por qué la Luna siempre muestra la misma cara a la Tierra.
- Estudió el sistema de Júpiter en 1766 y el problema de los tres cuerpos en 1772.
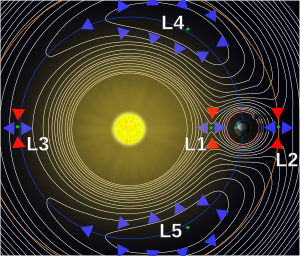
- En 1772, al intentar resolver el Problema de los tres cuerpos, descubrió los puntos de Lagrange. Estos son lugares en el espacio donde la gravedad de dos cuerpos grandes (como la Tierra y el Sol) se equilibra, permitiendo que un objeto pequeño permanezca en una posición estable. En estos puntos se han encontrado asteroides troyanos y satélites troyanos de Saturno.
- En 1773, estudió la ecuación secular de la Luna y la idea del potencial (una forma de calcular la atracción gravitatoria).
- También trabajó en cómo determinar la órbita de un cometa con solo tres observaciones (1778 y 1783).
- Entre 1781 y 1784, calculó cómo cambian las órbitas de los planetas a lo largo del tiempo.
Aportes al álgebra
La mayoría de sus trabajos sobre álgebra los envió a la Academia de Berlín.
- Estudió cómo resolver ecuaciones con números enteros (1769, 1770).
- Desarrolló métodos para resolver ecuaciones algebraicas de cualquier grado (1770 y 1771).
- En 1773, trabajó con los determinantes, que son herramientas matemáticas usadas para resolver sistemas de ecuaciones.
- Un teorema importante que lleva su nombre dice que si tienes un grupo de elementos (como un conjunto de números con una operación), el tamaño de cualquier subgrupo (un grupo más pequeño dentro del grande) siempre divide al tamaño del grupo principal.
Ecuaciones diferenciales
Lagrange inventó el método de variación de los parámetros, una técnica muy poderosa para resolver ecuaciones diferenciales (ecuaciones que involucran funciones y sus cambios). Por este método y sus muchas otras contribuciones, es considerado uno de los matemáticos más grandes de todos los tiempos.
Teoría de números
Lagrange también se interesó por la teoría de números, que estudia las propiedades de los números enteros.
- Demostró que cualquier número entero positivo que no sea un cuadrado perfecto puede escribirse como la suma de dos, tres o cuatro cuadrados de otros números enteros (1770). Esto se conoce como el Teorema de los cuatro cuadrados.
- Probó el teorema de Wilson (1771), que es una propiedad interesante de los números primos.
- Entre 1773 y 1777, demostró varios resultados que Fermat había enunciado pero no probado.
La mecánica analítica o lagrangiana
Entre 1772 y 1788, Lagrange reorganizó la mecánica clásica de Isaac Newton para hacerla más sencilla y fácil de calcular. Esta nueva forma se llama mecánica Lagrangiana y es la base de la mecánica analítica. Su gran libro, Tratado de Mecánica Analítica, recopila y unifica todo el conocimiento sobre mecánica desde Newton. Este libro es muy importante porque muestra cómo usar las ecuaciones diferenciales en la mecánica.
El objetivo de su libro era demostrar que toda la mecánica se basa en un solo principio. Desarrolló el método de las "coordenadas generalizadas", que es una forma muy inteligente de describir el movimiento de un sistema. En lugar de seguir cada parte por separado, mostró que si se describe el sistema con un número suficiente de variables, se pueden obtener las ecuaciones de movimiento de forma más sencilla.
Lagrange pensaba que la mecánica era una rama de las matemáticas puras, como una geometría de cuatro dimensiones (el tiempo y las tres coordenadas del espacio). Al principio, ninguna editorial quería publicar su libro, pero Legendre convenció a una empresa en París para que lo hiciera en 1788.
Teoría de funciones analíticas
Sus clases en la École polytechnique se centraron en el cálculo diferencial, que fue la base de su libro Théorie des fonctions analytiques, publicado en 1797.
En este trabajo, Lagrange intentó evitar el uso de cantidades "infinitamente pequeñas" o "infinitamente grandes" en el cálculo diferencial, que eran difíciles de entender para algunos filósofos. Sus trabajos en esta área fueron el punto de partida para las investigaciones de otros grandes matemáticos como Cauchy y Jacobi.
Fracciones continuas
Su libro Résolution des équations numériques, publicado en 1798, también surgió de sus clases. En él, presentó un método para encontrar las soluciones reales de una ecuación usando fracciones continuas. También demostró el pequeño teorema de Fermat, que es una propiedad de los números primos.
Su legado en la matemática pura
Lagrange se interesaba principalmente por la matemática pura, buscando resultados abstractos y generales. Dejaba las aplicaciones prácticas a otros. Por ejemplo, muchos de los descubrimientos de su colega Laplace fueron aplicaciones de las fórmulas que Lagrange había desarrollado.
Su forma de analizar los problemas era muy clara y brillante. Se dice que Lagrange tuvo un papel fundamental en el avance de casi todas las ramas de la matemática pura. Como otros grandes matemáticos, tenía un talento especial para la teoría de números, resolviendo muchos problemas y añadiendo nuevos teoremas. Creó el cálculo de variaciones y transformó el estudio de las ecuaciones diferenciales en una ciencia.
También contribuyó al cálculo de diferencias finitas con la fórmula de interpolación que lleva su nombre.
Reconocimientos y honores

- Fue miembro del Senado conservador desde 1799.
- Recibió el título de Conde del Imperio en 1808.
- Fue condecorado con la Legión de Honor y la Gran Cruz de la Orden de la Reunión.
- Está enterrado en el Panteón de París, un lugar de honor para grandes figuras de Francia.
- Su nombre está grabado en la Torre Eiffel junto a otros 71 científicos destacados.
- El cráter lunar Lagrange y el asteroide (1006) Lagrangea llevan su nombre en su honor.
- El punto de ingravidez entre la Tierra y el Sol, que él predijo, se llama «el punto de Lagrange L2».
- El operador matemático lagrangiano también lleva su nombre.
Véase también
 En inglés: Joseph-Louis Lagrange Facts for Kids
En inglés: Joseph-Louis Lagrange Facts for Kids
- Polinomio de Lagrange
- Mecánica Lagrangiana
- Puntos de Lagrange
- Multiplicadores de Lagrange
- Teorema de Lagrange